原创 线性系统理论的基础：线性代数

1.行列式是用来解方程的，它代表一个数，而矩阵是一个数表

２．行列式是ｎｘｎ，而矩阵可以不是方阵

３．余子式，从行列式中得来，在ｎ阶行列式中，把元素a_ij所在的第ｉ行和ｊ列划去后，余下的ｎ－１阶行列式，称为a_ij的余子式．

４．行列式是外加竖线，矩阵是外加方括号或者圆括号．

５．行矩阵又称行向量，列矩阵又称列向量．

６．零矩阵记作O.

７．ｎ阶方阵是矩阵．

８．单位矩阵记为 I  或 E .

９．矩阵乘法，只有当第一个矩阵的列数等于第二个矩阵的行数，两个矩阵才能相乘．

例如：４Ｘ３矩阵和３Ｘ５，编程４Ｘ５矩阵．

１０．方阵的行列式：由ｎ阶方阵Ａ的元素所构成的行列式，记作|A|或detA.

１１．逆矩阵．a^-1= 1/a成为ａ的逆．

在矩阵的运算中，单位矩阵Ｅ相当于１，如何AB=BA=E,那么Ｂ是Ａ的逆矩阵，记作A^-1=B

１１．１　奇异矩阵

|A|=0,称为奇异矩阵，否则称为非奇异矩阵．

１２．伴随矩阵 adj(A)

１３．齐次方程和非齐次方程

１４．在线性代数里， 向量空间的一组元素称为线性无关 (或称线性独立 )，如果其中没有向量可表示成有限个其他向量的线性组合
，反之称为线性相关 。 例如在三维欧几里得空间 R 3的三个向量(1, 0, 0)，(0, 1, 0)和(0, 0, 1)线性无关。 但(2,
?1, 1)，(1, 0, 1)和(3, ?1, 2)线性相关，因为第三个是前两个的和。

１４．１线性相关或线性无关的理解

使用状态空间方法分析问题时，需要列出一组方程．

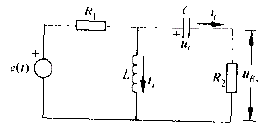
如下图，列方程，可以看出ＬＣ是线性无关的，可以列出两个不同的方程，而如果LC是线性相关的，那么仅可以列出一个独立的方程，因为用Ｌ可以表示出Ｃ，或者用Ｃ可以表示出Ｌ