原创 什么是Gamma

Gamma补偿：
对RGB三基色发光二极管(LED)温度特性的测试和分析发现,随着环境温度的变化,每种基色的LED亮度与常温时的亮度相比都会发生一定程度的偏移,
且其偏移量不相同,导致了图像白场平衡的失真.为了校正失真,针对每个基色LED提出一种不同环境温度下的Gamma补偿曲线,使RGB三基色LED在环
境温度变化时具有相同的亮度偏移值,以保证白场平衡.本文提出的Gamma补偿技术克服了LED的温度特性引起显示屏图像的色彩失真和白场平衡的破坏,使
图像的色彩不会受环境温度的变化而失真.
Gamma曲线：
Gamma可能源于CRT（显示器/电视机）的响应曲线，即其亮度与输入电压的非线性关系。

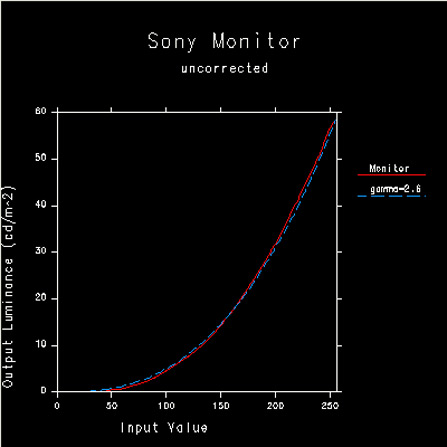
图：一典型显示器 的响应曲线，非常接近指数函数
(说明：上图中输入值为数字化的，即通常的RGB值，但可以理解数/模转换是线性的，所以它和输入电压是等效的)

　　归一化后，我们通常可以用一简单的函数来表示：

　　output = input ^ gamma

　　gamma就是指数函数中的幂。

图：归一化的Gamma曲线

　　注意上图曲线的一些特性：
　　* 端点是不变的，即不管gamma值如何变化，0对应的输出始终是0，1的输出始终是1（这一特性会被用到）。这可能是gamma又被叫作“灰度”系数的原因吧。
　　* gamma > 1时，曲线在gamma=1斜线的下方；反之则在上方。

　　另外说明一下，虽然是以显示器作为例子，但可扩展到一般的图像相关的输入/输出设备。Gamma曲线应该是普遍存在的，即使它不是严格的指数关系，可能还是会这么通称。至少我知道的数码机机/摄像头里的sensor也存在gamma曲线及gamma校正。

　　2.2. 检查显示系统的Gamma值

　　在PC上，好像还没有什么软件方法可以得到系统的Gamma值（4.1会说明这一点）。有人做了一些图片，可以粗略估计。其原理和Adobe Gamma类似。

图：Gamma对照图

　
　使用方法：与Adobe
Gamma类似，即眯着眼，或站远点，或近视眼取下眼镜，总之当左边糊成一片，而右边某栏的亮度和左边相当时。注意：如果您没有做任何Gamma校正（没
有使用Adobe
Gamma之类的软件，或虽使用了但校正系数设为1.0），测得的才是显示器的Gamma，否则只能称为系统Gamma（或复合Gamma）。如笔者的
ACER AL1916W的GAMA值为2.0左右。

　　另外，通过显示器自带的ICC Profile是可以知道显示器的Gamma的，这个应该比较准。
Gamma校正：
   一个数字化的图片文件，到我们最终看到的图片，中间要经过许多环节。几乎在任何一个环节上，都可以加入一些变换，以改变最终输出和最初输入的关系（类似的，这种关系被称作系统Gamma或复合Gamma）。

　　比如，对gamma=2.5的显示器，在数据传递到显示器之前，将其做一个gamma=0.4的变换（比如对显卡缓存中的数据，d’ = d ^ 0.4），这样就能从总体上得到一个线性的关系。

　　注意这里有一点混乱。通常我们说做一个gamma=c的校正，意思是指做output = input ^ (1/c)的变换。有一个倒数关系。

图：Gamma校正示意图

　
　对于PC，显示器的Gamma是2.2左右（可能以前更多的是2.5，现在好像趋向2.2了），一般没有内置的校正，所以我们说Adobe
Gamma对Windows系统默认的校正系数2.2。对于MAC，显示器的Gamma是2.5，硬件内置了1.4的校正，所以它还需要
2.5/1.4~=1.8的校正才成为线性的。下文对各种系统下的gamma校正过程有更详细的说明。