原创［转］用8051做16位运算－02

 2008-8-21 09:57  3886 9 9 分类: MCU/ 嵌入式

16-Bit Addition

16-bit addition is the addition of two 16-values. First, we must recognize that the addition of two 16-bit values will result in a value that is, at most, 17 bits long. Why is this so? The largest value that can fit in 16-bits is 256 * 256 - 1 = 65,535. If we add 65,535 + 65,535, we get the result of 131,070. This value fits in 17 bits. Thus when adding two 16-bit values, we will get a 17-bit value. Since the 8051 works with 8-bit values, we will use the following statement: "Adding two 16-bit values results in a 24-bit value". Of course, 7 of the highest 8 bits will never be used--but we will have our entire answer in 3 bytes. Also keep in mind that we will be working with unsigned integers.

Programming Tip: Another option, instead of using 3 full bytes for the answer, is to use 2 bytes (16-bits) for the answer, and the carry bit ( C ), to hold the 17th bit. This is perfectly acceptable, and probably even preferred. The more advanced programmer will understand and recognize this option, and be able to make use of it. However, since this is an introduction to 16-bit mathematics it is our goal that the answer produced by the routines be in a form that is easy for the reader to utilize, once calculated. It is our belief that this is best achieved by leaving the answer fully expressed in 3 8-bit values.

Let's consider adding the following two decimal values: 6724 + 8923. The answer is, of course, 15647. How do we go about adding these values with the 8051? The first step is to always work with hexadecimal values. Simlply convert the two values you wish to add to hexadecimal. In this case, that is equivalent to the following hexadecimal addition: 1A44 + 22DB.

How do we add thes two numbers? Let's use the exact same method we used in primary school, and in the previous section:

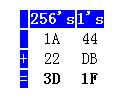
First, notice the difference. We are no longer working with a 1's, 10's, and 100's columns. We are just working with two columns: The 1's column and the 256's column. In familiar computer terms: We're working with the low byte (the 1's column) and the high byte (the 256's column). However, the process is exactly the same.

First we add the values in the 1's column (low byte): 44 + DB = 11F. Only a 2-digit hexadecimal value can fit in a single column, so we leave the 1F in the low-byte column, and carry the 1 to the high-byte column. We now add the high bytes: 1A + 22 = 3C, plus the 1 we carried from the low-byte column. We arrive at the value 3D.

Thus, our completed answer is 3D1F. If we convert 3D1F back to decimal, we arrive at the answer 15647. This matches with the original addition we did in decimal. The process works. Thus the only challenge is to code the above process into 8051 assembly language. As it turns out, this is incredibly easy.

We'll use the following table to explain how we're going to do the addition:

Since we're adding 16-bit values, each value requires two 8-bit registers. Essentially, the first value to add will be held in R6 and R7 (the high byte in R6 and the low byte in R7) while the second value to add will be held in R4 and R5 (the high byte in R4 and the low byte in R5). We will leave our answer in R1, R2, and R3.

Programming Tip: Remember that we mentioned above that the sum of two 16-bit values is a 17-bit value. In this case, we'll using 24-bits (R1, R2, and R3) for our answer, even though we'll never use more than 1 bit of R1.

Let's review the steps involved in adding the values above:

Add the low bytes R7 and R5, leave the answer in R3.
Add the high bytes R6 and R4, adding any carry from step 1, and leave the answer in R2.
Put any carry from step 2 in the final byte, R1.

We'll now convert the above process to assembly language, step by step.