原创［转］用8051做16位运算－05

 2008-8-21 10:12  3902 7 7 分类: MCU/ 嵌入式

16-Bit Division

16-bit division is the division of one 16-bit value by another 16-bit value, returning a 16-bit quotient and a 16-bit remainder. I used r1/r0 for dividend/remainder and r3/r2 for divisor/quotient.

Programming Tip: The number of bits in the quotient and the remainder can never be larger than the number of bits in the original divident. For example, if you are dividing a 16-bit value by a 2-bit value, both the quotient and the remainder must be able to handle a 16-bit result. If you are dividing a 24-bit value by a 16-bit value, the quotient and remainder must both be able to handle a 24-bit result.

So, again, let's remember how we did division in elementary school. For example, 179 divided by 8:

It's necessary necessary to follow this same process step by step. There is a 3-digit-dividend, so we expect 3 digits maximum for quotient. We "shift left" the divisor 2 digits (3-1) such that the number of digits in the divisor is the same as the number of digits in the dividend. So we get:

1 7 9 / 8 0 0 = ? ? ?

We divide the two numbers, multiply the result by the divisor and substract this result from the dividend. In this first step 179 can't be divided by 800, so the the result is 0. We subtract 0 from 179 and still have 179:

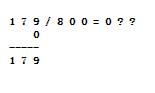
We then "shift right" the divisor 1 digit and repeat the process. 179 divided by 80 results in an answer of 2. After we subtract 160 (2x80) we are left with a remainder of 19:

We repeat the process again until the divisor has shifted into its original position:

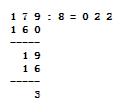
This may have been an unnecessary review of elementary school math, but it is important to remember exactly how the process is performed because we do exactly the same with the 8052 in binary system.

In this routine we will place the original dividend into R1 (high-byte) and R0 (low-byte) and the divisor in R3 (high-byte) and R2 (low-byte).

In the case of our example (179 divided by 8), the initial registers would be:

R1/R0 00000000 10110011
R3/R2 00000000 00001000

In the case of our example, once the above code is executed the registers will be as follows (including the carry bit 'C'):

C/R1/R0 0 00000000 10110011
C/R3/R2 1 00000000 00000000

At this point we can do the division itself. As we are in binary mode there is no need for a real division--it's just a comparison. At this point it's important to know the steps from above.

To see how the loop works here are the registers after each step:

1 r1/0 00000000 10110011 ;dividend
  r3/2 10000000 00000000 ;divisor
  r5/4 00000000 00000000 ;result

2 r1/0 00000000 10110011 ;dividend
  r3/2 01000000 00000000 ;divisor
  r5/4 00000000 00000000 ;result

...

8  r1/0	00000000 10110011 ;dividend
   r3/2	00000001 00000000 ;divisor
   r5/4	00000000 00000000 ;result

9  r1/0	00000000 00110011 ;dividend
   r3/2	00000000 10000000 ;divisor
   r5/4	00000000 00000001 ;result

10 r1/0 00000000 00110011 ;dividend
   r3/2 00000000 01000000 ;divisor
   r5/4 00000000 00000010 ;result

11 r1/0 00000000 00010011 ;dividend
   r3/2 00000000 00100000 ;divisor
   r5/4 00000000 00000101 ;result

12 r1/0 00000000 00000011 ;dividend
   r3/2 00000000 00010000 ;divisor
   r5/4 00000000 00001011 ;result

13 r1/0 00000000 00000011 ;dividend
   r3/2 00000000 00001000 ;divisor
   r5/4 00000000 00010110 ;result

STOP!

Register "B" is zero at this point. The remainder is already in R1/R0, and it is 3 decimal, same as above. The result is still in R5/R4, but we can see it's correct, too (10110b=22d). To finish the routine, we just "clean up" by moving R5/R4 to R3/R2.

We used small numbers here for easier explanation. Of course it works also with 16-bit numbers, that's what it was designed to do.

Taken as a whole, the above division algorithm can be converted into an easy-to-use function that can be called from your program. To call this function, you should pre-load R1/R0 with the high/low value to be divided, and R3/R2 with the high/low value that the number is to be divided by.