


超宽带(UWB)通信技术因其自身的优良特性,比如灵活性和鲁棒性以及高精度测距能力,近年来发展迅猛。由于超宽带波形的频域带宽很宽,所以要求UWB脉冲波形必须能够与其他通信系统的空中接口波形友好共存。为了避免UWB通信系统与现有电子通信系统之间的干扰,美国联邦通信委员会(FCC)在2002年对超宽带信号的峰值发射功率谱密度(PSD)做了严格的规定。
为了满足FCC辐射模板的要求,脉冲波形设计是UWB的关键技术之一。超宽带波形设计的主要目的就是要使其功率谱密度满足FCC的限制且尽可能大地提高频谱利用率,或表述为脉冲功率谱密度尽可能地接近FCC辐射模板上限。在超宽带系统设计中最常用的波形是高斯(Gauss)脉冲以及高斯各阶导函数脉冲。单一的高斯脉冲容易产生,但不能满足FCC的频谱规范,其导函数在很大程度上有所改善,但是频谱利用率不高,利用N个高斯导函数的线性组合,调整叠加系数可以达到较高的频谱利用率。此外,可用于超宽带波形的还有正交小波,Rayleigh脉冲,正交的Hermite脉冲以及椭球波函数PSWF。
本文采用Coiflets正交小波设计了超宽带脉冲波形。采用正交小波的原因是考虑多用户问题,利用Coiflets正交小波的平移正交性和尺度正交性,可以由小波基函数产生一系列具有相似时宽与相似带宽的波形,分配给不同用户,可以大大降低用户间干扰;而且通过对Coiflets小波压缩或平移后进行叠加,可进一步提高频谱的利用率。
2 Coiflets正交小波及组合波形
2.1 正交小波及其特性
 |
 |
由式(3)和式(4)可以看出,正交小波的正交性表现在平移正交性和尺度正交性两个方面。平移正交性是指不同波形在时间上进行适当平移后所得到的波形与当前波形是正交的;尺度正交性是指波形在时域进行压缩或者展宽所得到的波形与原波形是正交的。如:![]() ,则平移正交性表现在Ψ0,0(t)与Ψ0,1(t)是正交的;尺度正交性表现在Ψ0,0(t)与Ψ1,0(t)是正交的。
,则平移正交性表现在Ψ0,0(t)与Ψ0,1(t)是正交的;尺度正交性表现在Ψ0,0(t)与Ψ1,0(t)是正交的。
2.2 各种正交小波比较
常用的正交小波函数有Harr小波,Daubeehies小波,Coiflets小波,Symlets小波和Meyer小波。其中,Harr小波是正交,双正交且是紧支撑的,但它是离散的;Daubeehies小波不具有对称性,没有明确的表达式,在时域上是有限支撑的,Ψ(t)和Φ(t)支撑长度为6N-1;coif N小波系,是正交,双正交且是紧支撑的,Ψ(t)和Φ(t)支撑长度为6N-1,比db N小波具有更好的对称性;Meyer小波不是紧支撑的,但是它收敛速度快,Ψ(t)无限可微。为了研究信号在局部频率以及局部时间段的性质,希望所选的基函数应能同时具有时域和频域的定位功能,而且超宽带的带宽限制也要求频域限制在一定范围,所以小波函数应该具有紧支撑性。
2.3 Coiflets正交小波特性
Coiflets小波简记为coif N,N=1,2,…,5。coil N是正交、双正交小波,且是紧支撑的,支撑范围为6N-1,也是接近对称的。小波函数Ψ(t)的消失矩是2N,尺度函数Φ(t)的消失矩是2N-1。消失矩越大,它的支撑长度就越大,通常支撑长度不少于2N-1;消失矩越大,对应的滤波器越平坦,而且小波函数的振荡很强。光滑函数在利用小波展开后的零点越多,也就是说小波的消失矩的大小,决定了小波逼近光滑信号的能力。
选用Coiflets小波的原因:
(1)Coiflets小波有良好的正交与双正交特性;
(2)Coiflets小波在时域和频域都具有良好的紧支撑性和消失矩;
(3)Coiflets小波的频谱利用率要比单一的高斯函数高。
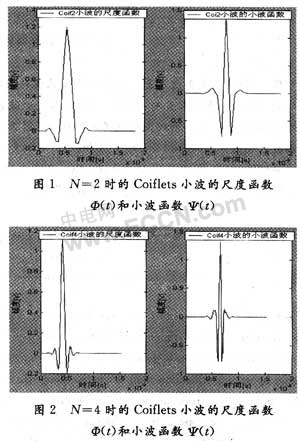
以N=2和N=4为例,它们的尺度函数Φ(t)和小波函数Ψ(t)分别如图1和图2所示。
 |
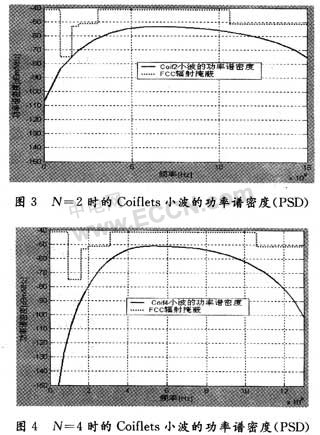
它们的功率谱密度分别如图3和图4所示。
 |
2.4 基于Coiflets小波的组合波形
 |
3 仿真结果
本文首先将单一的Coiflets正交小波脉冲与高斯二阶导函数与高斯五阶导函数脉冲进行比较,然后将Coiflets正交小波进行二阶叠加组合,如图5所示。单一的Coif 4小波选择的参数为:Coif 2小波函数的脉冲采样点数N为长度=45,Coif 4小波函数的脉冲采样点数N为长度=93,脉冲持续时间T都是2 ns,采样频率fs为30 GHz。选择函数Ψ(t)=Ψ0,0(t)+Ψ1,1(t)+Ψ2.2(t),组合后波形选择的参数和单一波形的参数统一:脉冲采样点数N0为组合后波形Ψ(t)的长度=93,脉冲持续时间T0=2 ns,采样频率fs为30 GHz。
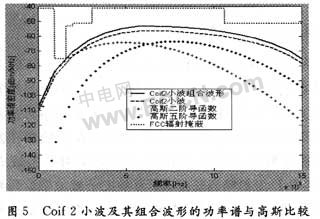 |
由图6中可以看出,单一的Coiflets小波函数脉冲的功率谱密度比高斯二阶导函数脉冲和高斯五阶导函数脉冲的功率谱密度能更好地符合FCC规定的频谱模板,叠加组合以后所得到的波形能非常好地满足频谱模板,在超宽带3.1~10.6 GHz范围内频谱利用率很高,比高斯二阶导函数脉冲和高斯五阶导函数脉冲以及单一的Coiflets小波函数脉冲都要好很多。
 |
4 结 语
本文基于Coiflets正交小波研究了UWB信号成形脉冲,利用正交小波的平移正交性和尺度正交性,由基函数生成一系列正交小波的函数,并进行组合叠加获得UWB脉冲波形。通过仿真,验证了设计的单一的正交Coiflets小波脉冲以及它们组合叠加后获得的正交脉冲的功率谱满足FCC频谱模板的限制,其频谱利用率优于高斯二阶导函数脉冲和高斯五阶导函数脉冲,且可以用于多用户超宽带无线通信系统。
 /5
/5 
文章评论(0条评论)
登录后参与讨论