实现的Montgomery大数相乘,如图所示; 供上一级ModExpPoweringladder 使用。
所谓的蒙哥马利形式即为模n的余数表示形式,只有当操作数转换为蒙哥马利形式时,才能使用此算法执行模乘。计算之后,操作数需要转换回正常表示。由于这些前、后计算步骤,蒙哥马利乘法并不比常规模乘快。但是,重复使用MonPro的情况下相比可以显著提高速度。当r是2的幂次时,除法可以用移位代替,余数的计算简化为位运算。n0为顶层模块中计算完成后給入的,其公式如下:
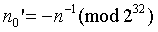
MonPro模块共8个端口,6进2出,inp轮流输入两个乘数,outp输出积。
端口名称 | 位宽 | 方向 | 描述 |
clk | | Input | 同ModExpPowering时钟 |
reset | | Input | 重置位 |
start | | Input | 启动标志位 |
n0_data | 64 | Input | 第一组n |
n_data | 64 | Input | 存储器給入n |
inp | 64 | Intput | 两乘数轮流由此输入 |
state | 5 | Output | 显示状态机运行状态 |
outp | 64 | Output | 乘积输出 |
MonPro模块端口定义
MonPro模块为ModExpPowering的次级调用,包含一个有10个状态的有限状态机,首先通过端口inp依次读入64位的乘数x与y,z则会初始化为0。
第一步通过例化MulAdd模块计算
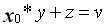
;
第二步把v的最低权重位记为,这里为64位,计算得到64位
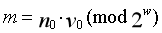
中间量m;
第三步MulAdd模块计算
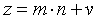
, 紧接着第四步完成
, ...
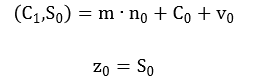
...
运算64次之后移位约减,得到32轮中的第一轮64位输出结果z;下面继续从第一步开始做循环32次,即可得到完整的2048位Montgomery输出。
作者: 指的是在下, 来源:面包板社区
链接: https://mbb.eet-china.com/blog/uid-me-3880846.html
版权声明:本文为博主原创,未经本人允许,禁止转载!



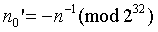

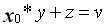 ;
;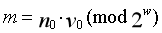 中间量m;
中间量m;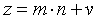 , 紧接着第四步完成
, 紧接着第四步完成 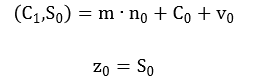 ...
...
 /1
/1 
pidaneng 2020-9-11 08:48