


【如果我写的好,请顶一下】
参加比赛或是做项目也好,PID的应用非常的广,不但可以用在运动控制的电机调速,更可以用在温度控制、电流控制、电压控制等等动态变量的控制。
PID其实没有多么神秘,还是那句话:被控量比我们的预期量(输入量)大,CPU就控制其小点;被控量比我们的预期量小,CPU就控制其大些。在这其中在引入被控量信号的变化率和误差累积,就成了真正的PID,可以达到非常好的控制效果。
|
图1.1 一个伺服系统结构的例子 |
由图1.1可以看出来,一个基本的伺服系统由控制器、功率放大单元、执行机构、反馈传感器组成。控制器是按照一定的控制策略,综合输入量和反馈量,输出控制信号的逻辑装置,一般情况下使用工业计算机或是微型计算机系统(DSP、MCU等)来作为伺服系统的逻辑中枢;功率放大单元是将计算机输出的控制信号,转变成一定的功率信号来驱动执行机构;执行机构(图1.1中是电动机)是将控制器的控制信号转变为相应的物理量,可以是电动机(用于运动控制)、加热器(用于温度控制)、功率开关管(用于电流或电压控制)等等;反馈传感器(图1.1中是位置检测传感器)是将执行机构的状态转变为相应的电气信号,并反馈给控制器的装置,它可以是位置传感器(位置伺服系统)、速度传感器(速度伺服系统)、温度传感器(温度伺服系统)、电流传感器(电流伺服系统)、电压传感器(电压伺服系统)等等。
由伺服系统的原理框图1.1就可以看出,伺服系统通常是一个闭环系统。其工作流程可以简单的描述为:控制器接收外界的输入,计算相应的输出值给功率放大单元,功率放大单元将控制器的信号放大,驱动执行机构动作。反馈传感器采集执行机构或被控对象的状态,将状态信息反馈给控制器,控制器根据接收到的输入值和传感器反馈回来的反馈值,根据一定得控制策略(本论文中使用的是PID算法),进一步调整输出,使输出达到目标值(输入值)。
其中,控制器--CPU/MCU
功率放大--MOSFET/MCS33886/各种电机驱动芯片
反馈传感器--角度传感器(位置伺服系统)/旋转编码器(速度伺服系统)/温度传感器(温度伺服系统)/电流传感器(电流伺服系统)
为了便于讨论,我编写了一个上位机软件,实时对伺服系统的工作状态进行采集,而且还可以绘制出伺服系统的工作曲线。
根据偏差的比例(P)、积分(I)、微分(D)进行控制(简称PID控制),是控制系统中应用最为广泛的一种控制规律。实际运行的经验和理论分析都表明,这种控制规律对许多工业过程进行控制时,都能得到满意的效果。不过,用计算机实现PID控制,不是简单的将模拟PID控制数字化,而是进一步与计算机的逻辑判断功能结合,使PID控制更加灵活,更能满足生产过程提出的要求。
(1)采样周期应远小于过程的扰动信号的周期。
根据香农采样定理:采样频率应该大于或是等于信号最高频率成分的两倍。这个定理给出了采样频率选择的最底线。
(2)执行机构的类型。
在执行器的响应速度比较慢时,过小的采样周期将失去意义,因此可适当选大一点。 在计算机运算速度允许的条件下,采样周期短,则控制品质好。当过程的纯滞后时间较长时,一般选取采样周期为纯滞后时间的1/4~1/8。
(3)给定值的变化频率。
加到被控对象上的给定值变化频率越高,采样频率也应该越高,这样给定值的改变可以迅速得到反应。
(4)被控对象的特性
若被控对象是慢速的热工业或是化工对象时,采样周期一般取的比较的大;若被控对象是较快速的系统,采样周期应取得比较小。
(5)控制算法的类型
采用PID控制算法,积分(I)和微分(D)作用都与采样周期T的选择有关系。采样周期T太小,将使微分作用不明显。
一般来说,增加控制系统的比例增益,可以提高系统的响应速度,同时也会降低稳态误差。尽管如此,如果比例增益太大,系统超调就会增大,如果Kp再进一步增加,震荡就会加大,系统就会变得不稳定。
为了消除稳态误差,在控制器中必须引入“积分项”。积分项对误差进行累加,随着时间的增加,积分项会逐渐增大。这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。因此,比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。但积分过强同样影响系统的稳定性。
自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳。其原因是由于存在有较大惯性组件(环节)或有滞后(delay)组件,具有抑制误差的作用,其变化总是落后于误差的变化。解决的办法是使抑制误差的作用的变化“超前”,即在误差接近零时,抑制误差的作用就应该是零。这就是说,在控制器中仅引入“比例”项往往是不够的,比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势,这样,具有比例+微分的控制器,就能够提前使抑制误差的控制作用等于零,甚至为负值,从而避免了被控量的严重超调。所以对有较大惯性或滞后的被控对象,比例+微分(PD)控制器能改善系统在调节过程中的动态特性。但是,如果反馈回来的过程变量代表的噪声,微分参数就会引起系统的不稳定。
|
图3.1 位置型PID控制流程 |
在控制系统中,这种控制量确定了执行机构的位置,例如在阀门控制中,这种算法的输出对应了阀门的位置(开度)。所以,将这种算法称为“位置算法”。
|
图3.2 增量型PID控制流程图 |
如上图, 当执行机构需要的不是控制量的绝对值,而是控制量的增量(例如去驱动步进电动机)时,需要用PID的“增量算法”。
|
数字PID控制算法实现方式比较
在控制系统中,如果执行机构采用调节阀,则控制量对应阀门的开度,表征了执行机构的位置,此时控制器采用数字PID位置式控制算法;如果执行机构采用步进电机,每个采样周期,控制器的输出的控制量是相对于上次控制的增量,此时控制器应该采用数字PID增量式控制法。
虽然增量式控制法和位置式控制法更有应用领域,但是增量式控制法相对于位置式控制法,具有诸多的优势:
(1)增量式控制法不需要做累加,控制量增量的去定仅与近几次误差采样值有关,计算误差或计算精度等问题对控制量的影响比较的小。相比之下,位置控制法要用过去的误差的累加值,容易产生较大的累加误差。
(2)增量式算法得到的是控制量的增量。例如在阀门的控制中,只输出阀门开度的变化部分,误动作影响小,必要时通过逻辑判断限制或禁止本次输出,不会严重影响系统的工作。相比之下,位置式控制算法的输出是控制量的全量输出,误动作影响比较大。
(3)采用增量算法,容易实现手动到自动的无冲击切换。
下图给出了数字PID控制算法的控制流程图。增量式的控制流程和位置式的控制流程很相似。
| ||||||||
图3.3 PID程序流程
数字PID参数整定1 工程法整定PID参数的方法在工程上,PID参数整定的方法比较的多,分别有:凑试法、扩充曲线法、优选法、自整定法等等。由于研究采用的标定系统采样频率有限,不能绘制出非常精确响应曲线,所以使用扩充曲线法误差较大。下面的参数整定使用凑试法。 (1)首先整定比例环节 将比例系数由小到大的变化,并观察相应的系统响应,直到得到一个反应速度快、超调小的响应曲线。如果系统静差已经达到允许的范围,并且响应曲线已经令人满意,那么只是用比例控制器即可。这里确定的是最优比例系数。 (2)再加入积分环节 如果在比例部分不能有效地消除静差,需要加入积分环节。积分系数P的整定应该从大到小。并且应该将第一步整定的比例环节缩小(可以缩小为原来的0.8倍)。然后慢慢的减小积分常数,直到系统具有良好的动态性能,并且静差得以消除。 (3)最后加入微分环节 如果在使用比例积分控制器时,动态特性仍达不到要求,可以加入微分环节。在整定微分环节时,微分系数从小到大变化,在同时小范围改变比例、积分系数的同时,多次试凑,直到达到理想的控制效果。 2 数字PID参数整定过程由于机器人手臂定位属于绝对位置式定位,这里首先讨论位置式PID伺服系统的PID参数整定。 (1)采样周期的选择 首先,选择一个合适的采样周期。采样周期应该综合各方面考虑,首先研究的是一个位置伺服系统,要求响应快,精度高。因此采样周期不能太大。同时,电机带有减速机构,转动惯量比较的大,因此采样周期又不能太小。关于采样周期的选择,虽然有“香农定理”这样的规律,但是并没有给出实质的选择方法,大多是在规律的指导下探索。这里,本人总结了一个根据工程试验选择采样频率的方法。
如图3.4,是电机在额定电压下,连续旋转的位置传感器输出电压曲线。可以根据这个图大体的估算合适的采样频率。从这个图上的周期可见,电机(带减速机构)的额定转速为1.20转/秒,即约为430度/秒。假设我们的伺服系统要求分辨率在0.5度,那么可以计算出来,伺服系统要转过这0.5度最快需要0.5/430*1000=1.16ms。如果将0.5度看成是系统的一个“标准单位”,那么1.16ms就是系统控制的“标准时间”。假设,采样周期比这个“标准时间”还要大,就可能出现伺服系统转过了“目标点”,但是系统还没有检测到得现象。当然,这个假设中没有考虑系统的静摩擦、启动惯量等。但无论如何,不排除极限情况下,系统稳定性要求系统达到及时响应。因此,本人认为采样周期在一般情况下不要大于这个“标准时间”。接下来再综合考虑电机本体的转动惯量和静摩擦的存在,转动惯量和静摩擦越大,采样周期可以相应的越大一些;反馈传感器的精度越高,采样周期可以选的越小一些,这样有利于提高系统的控制精度。综上所述,采样周期可以选择稍小于“标准时间”,为1ms,即采样频率1KHZ。
(2)比例系数的整定 在选择了采样周期的情况下,开始整定比例(P)系数。比例系数从小到大变化。 P控制源代码: #define k 1 E[k]=TargetValue-ADValue; //计算当前偏差。 Uk=KP*E[k]; //计算比例部分。 Turn(Uk); //输出。 | ||||||||
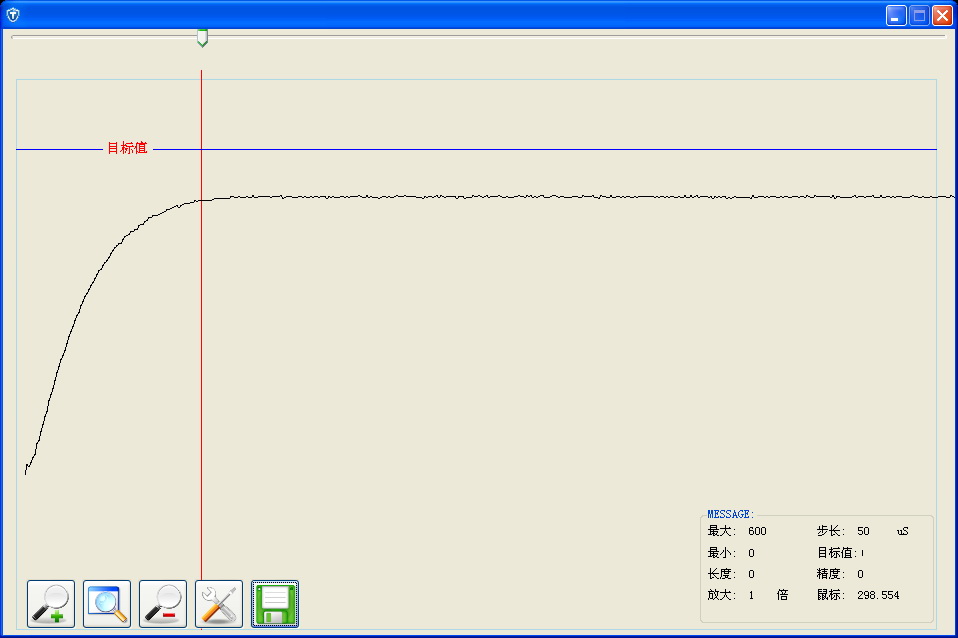
由以上的数据可以看出,增大比例系数Kp可以加快系统的响应,在有静差的时候有助于减小静差。但是过大的比例系数会使系统有较大的超调,并可能产生振荡。经过多次的试验,最终选择Kp=3。
(3)积分项的整定
如上图所示,在只使用积分(P)控制的时候,存在一定的静差,因此很有必要加入积分项,来消除这个静差。积分项的整定是从大到小整定,但是需要提前注意几个问题:
1.长时间的积分会造成积分饱和。
解决这个问题的办法是采用“积分分离”的办法,在误差较大的时候积分项不起作用,当误差范围在一定范围内以后积分才起作用。本人认为应该根据计算机的字长和传感器精度分析,计算出不会造成积分饱和的“积分时间”,来确定误差在多大的值时开始投入积分。
2.由于计算机精度问题,较小的误差将被舍掉,而不能输出。
解决这个问题的方法除了使用更加精确地AD/DA外,还可以采用误差累计的方法,当误差累计到一定程度,进行一次积分输出,而不是将小误差舍弃掉。为了避免小误差的浮点累计运算,本人使用了一个方法:“倍乘法”。即将小数误差乘以一定得倍数,比如10倍。这样,小数被转换成了整数,积分项的运算也转换成了整数运算。最后在输出之前,将Uk的值再除以10。
PI控制源代码:
#define k 1
E[k]=TargetValue-ADValue; //计算当前偏差。
if(abs(E[k])<50) //在一定范围内才投入积分
{
SumErr+=E[k];
SumErr=SumErr>20000?20000:SumErr;
}
Else SumErr=0; //清除积分累加。
Uk=KP*E[k]+SumErr/KI; //计算比例+积分。其实1/KI才是积分常数。
Turn(Uk); //输出。
如上面的组图所示,积分作用有助于消除系统误差,但是过大或过小的积分系数都将使系统品质降低。经过反复试凑,最终选取积分常数KI=0.003。
(4)微分项的整定
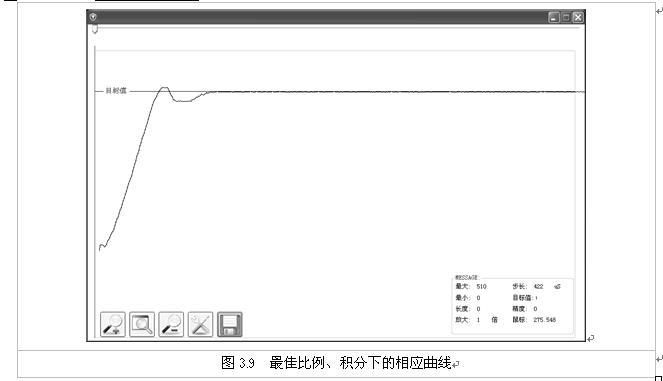
以上的PI控制器,从图3.9的响应曲线上来看,已经达到了令人满意的效果。系统的静差已经基本消除,系统运行已经基本满足要求。但是系统仍然存在不能忽略的超调,有时候这种超调会让机器人手臂的定位感觉非常的僵硬,因此需要进一步将其去掉。
PID控制源代码:
#define k 1
E[k]=TargetValue-ADValue; //计算当前偏差。
if(abs(E[k])<50) //在一定范围内才投入积分
{
SumErr+=E[k];
SumErr=SumErr>20000?20000:SumErr;
}
Else SumErr=0; //清除积分累加。
Uk=KP*E[k]+E[k]/KI+KD*(E[k]-E[k-1]); //计算比例+积分+微分。
Turn(Uk); //输出。
E[k-1]=E[k]; //更新E[k-1]
从图3.11中的图像对比中,可以发现微分作用避免了被控量的严重超调,合适的微分项使得系统超调变小,改善了系统在调节过程中的动态特性。经过多次试凑,确定PID的参数为KP=3,KI=0.003,KD=40。
用户1318783 2012-7-14 13:50
用户367120 2011-8-7 18:00
用户1401226 2010-5-12 14:15
liangjlong_779189698 2010-1-3 22:00
用户1503317 2009-12-17 11:17
用户483681 2009-11-2 15:07
用户483681 2009-11-2 15:06
用户214676 2009-7-24 15:26
uzufk_681520805 2009-6-30 13:35
用户1398993 2009-6-28 22:08