标签: 浅层神经网络

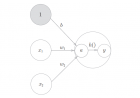
回顾： 【零基础】AI神经元解析（含实例代码） 一、序言 　　前两天写了关于单神经元的解析，这里再接再厉继续浅层神经网络的解析。浅层神经网络即是“层次较少”的神经网络，虽然层次少但其性能相对单神经元强大了不只一点。 　　注：本文内容主要是对“床长”的系列教程进行总结，强烈推荐“床长”的人工智能系列教程（https://www.captainbed.net/） 二、浅层神经网络的构成 　　回顾前面单神经元的构成，我们知道神经元包含4个关键函数： 　　1）传播函数，由输入x、偏置w、阈值b计算出a 　　2）激活函数，将a映射到0~1之间的结果y，可理解为（是、否）的概率 　　3）反向传播函数，通过y、答案label计算出dw、db（用以更新w和b） 　　4）损失函数，计算y与label间的误差 　　直观上我们知道浅层神经网络自然是由数个神经元构成的，对于一个简单的两层神经网络其结构如下图所示： 　　它包含了输入层（即X）、隐藏层、输出层，其中输入层不是神经元，所以说这是一个两层的神经网络。 　　在实际实现时我们并不是挨个计算每一个经元的结果，最后再计算输出的结果。我们是一次计算出一层所有的神经元结果，再将每一层的结果作为输入计算下一层。而且第一层的传播函数并不与第二层传播函数分离，神经网络的传播函数包含了所有层的传播计算，反向传播函数也是包含了所有层的反向计算，所以从单神经元到神经网络代码的结构其实变化不大。 　　下面我们直接上代码来解析，如果你看明白了前面单神经元的解析，那这里是非常好理解的。 　　 （文末附完整代码下载方式） 三、准备工作 　　 1）要处理的问题 　　之前我们用单神经元要处理的问题是“从图片中识别出数字9”，即使使用单神经元也有93%的正确率，所以这里我们要增加问题的难度。将问题改为“从图片中识别出奇数”，代码上只需要很小的修改，将下面代码 　　#将label不是9的数据全部转为0，将9转为1 　　train_label = np.where(train_label==9,1,0) 　　test_label = np.where(test_label==9,1,0) 　　修改为： 　　#找出图片中的奇数将label中13579置为1、02468置为0 　　train_label = np.where((train_label%2)!=0,1,0) 　　test_label = np.where((test_label%2)!=0,1,0) 　　使用之前的单神经元代码执行后的结果为下图所示，可以看到预测效果大幅下降。 　　 2）要使用的网络结构 　　首先要明确神经网络的层数，这里我们是一个简单的网络，所以只需要两层。其次是每一层神经元的个数，这里我们网络第一层设置4个神经元，第二层是输出层所以只要一个神经元。输入层跟以前一样，是784个输入（一张28x28图片的所有像素），网络结构如下图： 四、随机初始化参数 #初始化参数w和b def initialize_parameters(input_num, hide_num, out_num): 　　#input_num 输入层神经元个数 　　#hide_num 隐藏层神经元个数 　　#out_num 输出层神经元个数 　　np.random.seed(2) 　　#随机初始化第一层相关参数w、b 　　W1 = np.random.rand(hide_num, input_num) * 0.01 　　b1 = np.zeros(shape=(hide_num, 1)) 　　#随机初始化第二层相关参数w、b 　　W2 = np.random.randn(out_num, hide_num) * 0.01 　　b2 = np.zeros(shape=(out_num, 1)) 　　return W1,b1,W2,b2 　　浅层神经网络与单神经元在初始化参数w、b的区别有以下几点： 　　1）每一层神经元使用不同的w和b，所以有w1、w2、b1、b2，如果是三层网络则相应会有w3、b3. 　　2）不同层神经元的w、b的数据形状是不一样的。比如我们输入的图片有784个像素，且第二层有4个神经元，所以第一层w的形状是（4,784）、b的形状是（4,1）。第二层神经元只有一个，来自第一层的输入只有4个参数，所以第二层w的形状是（1,4）、b的形状是（1,1）。 　　3）w1和w2是随机生成的，之前单神经元结构中，w初始值为0，如果这里还使用全0的话，最终结果可能与单神经元一样，而且还乘以0.01确保初始值足够小。 五、传播函数 #向前传播函数 def forward(img, W1,b1,W2,b2): 　　#第一层 　　A1 = np.dot(W1, img) + b1 　　Y1 = np.tanh(A1)#第一层和第二层使用不同的激活函数 　　#第二层 　　A2 = np.dot(W2, Y1) + b2 　　Y2 = sigmoid(A2) 　　return Y1,Y2 　　传播函数与单神经元结构类似，不过需要注意的是，这里第一层使用的激活函数为tanh、第二层依旧使用的是sigmoid。他们的区别在于，sigmoid是将输出映射到0~1而tanh是将输出映射到-1~1。具体原因和区别以后再说（因为我也没搞清楚呢），这里只要知道有区别就行了。 六、反向传播函数 #反向传播函数 def backward(img, label, W1,b1,W2,b2, Y1,Y2): 　　m = img.shape 　　#第二层 　　dZ2 = Y2 - label 　　dW2 = np.dot(dZ2, Y1.T)/m 　　db2 = np.sum(dZ2, axis=1, keepdims=True)/m 　　#第一层 　　dZ1 = np.multiply(np.dot(W2.T, dZ2), 1-np.power(Y1, 2)) 　　dW1 = np.dot(dZ1, img.T)/m 　　db1 = np.sum(dZ1, axis=1, keepdims=True)/m 　　return dW1,db1,dW2,db2 　　与传播函数方向相反，这里是先计算第二层的反向传播再计算第一层的反向传播。需要注意的是，由于第一层使用的激活函数是tanh，所以其反向计算公式与第一层的公式不一样，因为使用不同激活函数其反向求导也就不一样了。 　　另外np.sum中的两个参数axis=1、keepdims=True是为了确保db1的数据形式为（1,4），其中axis=1的意思是按行求和、keepdims=True的意思是保留矩阵的形状，不同参数的np.sum计算示意如下： 　　np.sum(dZ1)/m　　　　　　　　　　　　　　　 0.0016664927232987162 　　np.sum(dZ1, axis=1)/m　　　　　　　　　　　　 　　np.sum(dZ1, axis=1, keepdims=True)/m　　　 　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 ] 七、梯度下降 #梯度下降 更新w、b参数 def update(W1,b1,W2,b2, dW1,db1,dW2,db2, learning_rate=1.2): 　　W1 = W1 - learning_rate*dW1 　　b1 = b1 - learning_rate*db1 　　W2 = W2 - learning_rate*dW2 　　b2 = b2 - learning_rate*db2 　　return W1,b1,W2,b2 　　梯度下降与单神经元的情况差不多。 八、损失函数 #损失函数 def costCal(Y2, label): 　　m = label.shape 　　logprobs = np.multiply(np.log(Y2), label) + np.multiply((1-label), np.log(1-Y2)) 　　cost = -np.sum(logprobs)/m 　　return cost 　　损失函数与单神经元的情况也差不多，需要注意的是np.multiply就是将两个矩阵做对应元素的乘。 九、预测函数 #预测函数 def predict(W1,b1,W2,b2, img): 　　Y1,Y2 = forward(img, W1,b1,W2,b2) 　　predictions = np.round(Y2)#对结果四舍五入 　　return predictions 　　与单神经元的情况类似，预测函数其实就是做一次“向前传播”。 十、训练模型并预测 #训练模型 def model(img, label, hide_num, num_iterations = 1000, learning_rate=0.1, print_cost = False): 　　np.random.seed(3) 　　input_num = img.shape 　　out_num = label.shape 　　#初始化参数 　　W1,b1,W2,b2 = initialize_parameters(input_num,hide_num,out_num) 　　#循环若干次完成训练 　　for i in range(0, num_iterations): 　　　　#向前传播 　　　　Y1,Y2 = forward(img, W1,b1,W2,b2) 　　　　#计算本次成本 　　　　cost = costCal(Y2, label) 　　　　#反向传播，得到梯度 　　　　dW1,db1,dW2,db2 = backward(img, label, W1,b1,W2,b2, Y1,Y2) 　　　　#参数优化 　　　　W1,b1,W2,b2 = update(W1,b1,W2,b2, dW1,db1,dW2,db2, learning_rate) 　　　　# 将本次训练的成本打印出来 　　　　if print_cost and i % 100 == 0: 　　　　print ("在训练%i次后，成本是: %f" % (i, cost)) 　　return W1,b1,W2,b2 #调用训练模型 W1,b1,W2,b2 = model(train_img, train_label, 4, num_iterations=2000, learning_rate=1, print_cost=True) #调用预测函数 predictions = predict(W1,b1,W2,b2, test_img) print ('预测准确率是: %d' % float((np.dot(test_label, predictions.T) + np.dot(1 - test_label, 1 - predictions.T)) / float(test_label.size) * 100) + '%') 　　需要注意的是这里的learning_rate=1，而单神经元时的learning_rate为0.005。 十一、总结回顾 　　通过实现一个简单的二层神经网络我们发现，其实代码并没有修改很多，整体的结构也变化不大，其中最主要的变化在于第一层使用的激活函数变为tanh，由此导致反向传播的计算也有了较大的变化。 　　运行后我们可以发现，预测的准确度较单神经元有了较大幅度的提升： 在训练0次后，成本是: 0.693817 在训练100次后，成本是: 0.251725 在训练200次后，成本是: 0.176756 在训练300次后，成本是: 0.110538 在训练400次后，成本是: 0.372297 在训练500次后，成本是: 0.128188 在训练600次后，成本是: 0.091792 在训练700次后，成本是: 0.075769 在训练800次后，成本是: 0.064764 在训练900次后，成本是: 0.055826 在训练1000次后，成本是: 0.132452 在训练1100次后，成本是: 0.102556 在训练1200次后，成本是: 0.131425 在训练1300次后，成本是: 0.086445 在训练1400次后，成本是: 0.178343 在训练1500次后，成本是: 0.077496 在训练1600次后，成本是: 0.093846 在训练1700次后，成本是: 0.071567 在训练1800次后，成本是: 0.070109 在训练1900次后，成本是: 0.060202 预测准确率是: 94% 　　 关注公众号“零基础爱学习”回复"AI5"可获得完整代码 。后面我们还会继续更新“如何构建深度神经网络”，以及对目前还未明晰的问题解析。