标签: 梯度校验

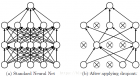
一、序言 　　dropout和L1、L2一样是一种解决过拟合的方法，梯度检验则是一种检验“反向传播”计算是否准确的方法，这里合并简单讲述，并在文末提供完整示例代码，代码中还包含了之前L2的示例，全都是在“深层神经网络解析”这篇基础之上修改的。 二、dropout 　　简单来说dropout就是在每次训练时“随机”失效网络中部分神经元，大概就是下图这么个意思。 　　让神经元随机消失办法很简单，我们将每一层的输出Y中部分位，置为0即可。回顾一下神经元的输出值Y： 　　A = np.dot(w, IN) + b 　　Y = relu(A) 　　对于输入层，IN就是img，对于其他层IN就是上一层的输出Y，A是权重w与输入IN的矩阵乘积，Y是A在0-1间的映射，表示概率。对于w与IN的乘积运算，我们若在IN中插入若干个0值，其计算结果（相乘后是累加）对下一层是没有影响的，所以将IN（Y）中某些位置为0就相当于将上一层某些神经元删除了。 　　具体到实现上，先按Y的形状生成0-1的随机数 　　D = np.random.rand(Y.shape , Y.shape ) 　　接着将小于keep_prob的数全部置为0其他的置为1，keep_prob就是删除的神经元比例，如0.5就删除50%。 　　D = D < keep_prob 　　然后用Y乘以D，按keep_prob的比例删除输出值（也即是下一层的输入）。 　　Y = Y * D 　　最后还需要用Y除以keep_prob，目的是将训练和测试时的“期望”保持一致。 　　Y = Y / keep_prob 　　简单理解“期望“就是在训练时我们删除了一定比例的神经元，但是实际使用时这些神经元可都是在的，所以Y除以keep_prob就是让二者的”期望“保持一致。 　　这里我们简单讲了下过程，具体的实现在文末可以下载完整代码。 三、梯度校验 　　梯度校验基于这么一个事实：神经网络是一个“混沌”系统，增加一些参数、减少一些参数、写错一些参数，又比如前面dropout方法中删除一些神经元对整体网络的运行似乎没有影响，你不会得到一个明确的报错，有时训练得到的结果表现的可能还不错（有时甚至更好了）。我们需要一些手段来做一些“基本”的检测吧？ 　　梯度校验就是这么一个“基本检测”，他的原理是“用另一种路径”来重新计算Δw，如果你计算的Δw与反向传播计算的Δw“差不多”，那说明大方向上你的网络是OK的，至少“优化”的方向是正确的。 　　我们知道Δw的计算是在损失函数的基础上对w进行求导，求导的结果即是w优化的方向（使cost趋向于0）。 　　在“反向传播”的解析中，我们的损失函数公式是标签值减去预测结果： 　　cost = ( Label - Y )^2 　　而后用cost对w求导可以得到Δw使cost值趋向于0： 　　Δw = ( Label - Y )*X 　　上式是利用对cost求导得到的，验证上式计算结果是否正确的另一种路径则是回归“求导”的本质：当自变量的增量趋于零时,因变量的增量与自变量的增量之商的极限。用数学公式表达出来就是： 　　cost = J(w) =( Label - Y )^2 　　Y = wX + b 　　 　　上式中a是一个趋向于0的极小值，我们可以随便取一个，比如10的-7次方（0.0000001）。上式中J(w+a)和J(w-a)可以通过向前传播和损失计算得到，这种方式可以称为极值法，而后与反向传播求得的Δw作比较，下式是一个比较科学的比较方法（二范数）： 　　 　　其中grad是反向传播求得的Δw，gradapprox是极值法求得的Δw，difference称为误差。 四、多维神经网络的梯度检验 　　上一节简述了梯度检验的原理，然鹅放到实际应用时有点抓虾，因为前面的公式范例只能契合单神经元的情况，将公式应用到多层神经网络还需要做一些修改。最主要的修改在于，我们要将w、b、dw、db转为一维向量. 　　一个简单的w示例如下： 　　w = {'1': ,'2': ,'3': } 　　对于多层的神经网络来说，w+a、w-a不是将w中所有元素都加减a，而是每个元素依次操作，错误示例如下： 　　w + a ={'1': ,'2': ,'3': }　　#这个是错误的示范！！！ 　　正确的示例如下： 　　w + a ={'1': ,'2': ,'3': } 　　w + a ={'1': ,'2': ,'3': } 　　以此类推。 　　这个很好理解，如果使用错误示例中的方法，最后我们通过极值法计算出来的gradapprox只有一个元素，然鹅dw是有10个元素的。使用正确示例这个方法其实是对w中每一个位都按极值法求得了导数的近似值，正好对应了dw中每一个位的导数。 　　为了便于计算，我们可以将w和dw都转为一维向量： 　　w = 　　一维向量的好处是增减a时比较方便，实际计算损失时还得再转回多维的形状。具体代码实现在文末有下载方式，为了便于理解我只实现了dw的检验，实际上你可以把w、b拼成一个向量，dw、db拼成一个向量，使用极值法计算出梯度后可以做一个整体的比较（自己试试看）。 　　因为梯度校验速度真的非常非常慢，为了加快测试的速度，我们可以将网络做的更简单、将训练数据减少，实际使用时可以是所有训练数据都一起上，慢就慢点吧。 　　需要注意的是，如果你要做梯度校验，那dropout必须得先关掉（将keep_prob设为1），原因很好理解，dropout使神经网络在训练时随机“删除”了部分神经元，使用极值法计算Δw时需要做两次向前传播，两次随机删除的神经元肯定不一样，反向传播删除的神经元也不一样，自然最后计算的difference就不准确了。 五、总结 　　本文简单讲了下神经网络的优化方法dropout和反向传播的检验方法“梯度校验”，其中dropout需要与之前的L2优化结合起来看。 　　完整实现代码可以关注公众号“零基础爱学习”回复“AI10”获取。