标签: 传播函数

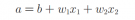
一、序言 　　之前已经写过“单神经元、浅层神经网络、深层神经网络”（感兴趣的可以翻翻），写的有点乱而且很多环节都没有说明白。这里我们尝试通过“感知机”的描述来回答一个问题：“为什么传播函数长这个样子”。 　　感知机是一种类似神经网络的预测模型，现在各种功能强大的神经网络正是在感知机的基础上诞生的，看懂感知机，神经网络也就不难了。另外，无论是感知机亦或是早期的神经网络，本质上他们都是用于处理“二分类”问题，本文就从二分类问题开始，反向推导出感知机模型。至于感知机是如何转变为神经网络以及更多的细节就留到以后再讲吧，欢迎关注“零基础爱学习”一起学习人工智能。 二、二分类 　　“二分类”只是一种叫法，可以将处理二分类问题的模型想象成一个黑盒子，无论输入什么内容，输出就是1或0（yes or no）。典型的二分类问题如下： 　　1）图中是否包含猫 　　2）图中是否包含小汽车 　　3）图中是否包含人像 　　如“图中的猫是什么颜色”这样的问题就不属于二分类了，因为猫可能是白色、黑色、黄色，甚至图中压根就没有猫。 　　这里我们考虑一个非常简单的二分类问题： 　　 “仅有4个像素的图片白不白” 　　下面随机生成了一张四个像素的图片（将像素放大了N倍方便观察） 　　对应的灰度值是（灰度值范围0-255，0表示全黑、255表示全白）： 　　X=(240,200,100,10) 　　要判断上述图片“白不白”直观上很好处理，我们将各像素的灰度值相加，当灰度值之和大于某个阈值a时我们就认为这是一张白图，小于a时就认为这不是一张白图。伪代码示例如下： a: 　　　　return 1 　　else: 　　　　return 0 　　但这种处理方式有个问题，它没有考虑到各像素不同表现形式对整体感官也是有一定影响的，如下面两张图： 　　其实两张图的灰度值之和是一样的，但主观上我们可能认为左边的图整体上较右边的图“白”一点。那我们换一种判断方式，将每一个像素的特征都考虑进来： a4: 　　　　return 1 　　else: 　　　　return 0 　　这里的a1、a2、a3、a4可以称为各像素的“特征”值，但此判断方法又导致通用性很差，比如我们调换一下各像素的位置，可能又需要新增一套特征值： b4): 　　　　return 1 　　else: 　　　　return 0 　　上面只使用了两套特征值，实际上4个像素的组合最多可能需要6套特征值。如果需要处理的是500x500的图片，那代码的复杂程度就不敢想象了。 　　通过前面的举例，我们会发现使用计算机来处理一个非常简单的二分类问题也非常困难，那就没有办法了吗？当然不是，前面无论是使用阈值或是特征值来做“白或不白”的判断，本质上是希望建立一个“确定系统”，然鹅现实世界往往并不是那么明确，“白与不白”的判断其实是个“混沌系统”，它受到了各种各样的因素影响。那么是否有办法将个体与整体相结合呢？聪明的先贤只做了一点微小的调整： a : 　　　　return 1 　　else: 　　　　return 0 　　这里a依然称为阈值，w1、w2、w3、w4是特征的另一种形式，这里称为权重。输入与权重相乘再累加的方式，即考虑到了“个体”在二分类判断中应有所区别，又考虑到了“整体”在判断中的决定性作用。但具体到每个个体在二分类判断中应当占有多少比重（权重的大小），最终阈值应当设置为多少合适，我们很难直接给出一个确定答案，于是感知机就该上场了。 三、感知机 　　一个简单的感知机模型如下图： 　　数学式为： 　　x1w1+x2w2 <= a　　则y=0（no） a　　 则y=1（yes） 　　x1、x2是输入，w1、w2是输入对应的权重，a是阈值，y是输出。 　　为便于使用，我们可以将a挪到式子的左边并用b=-a来代替，则数学式变为： 　　x1w1+x2w2+b <= 0　　 则y=0（no） 0　　　则y=1（yes） 　　然后我们将前面提出的二分类问题 “仅有4个像素的图片白不白” 套用到数学式中： 　　x1w1+x2w2+x3w3+x4w4+b <= 0　　则y=0（no） 0　　 则y=1（yes） 　　现在我们成功将一个二分类问题转变成了数学问题，回答二分类问题的答案就是找到一个恰当的w和b，寻找w、b的过程我们称为训练。这里需要注意的是，我们永远只能找到一个“凑合”的w和b值，即最终的感知机模型并不会完美契合所有训练数据。 　　现在我们再看一下神经网络中的传播函数： 　　是不是没那么难理解了？ 　　这里我们就不实现一个完整的感知机了，实际上代码与单神经元类似，整个过程也是向前传播、损失计算、反向优化，最终得到w、b值。 四、总结 　　本文尝试从二分类问题的角度来理解传播函数，但其真实的数学含义还是没有搞清楚，留到以后再说吧。 　　请关注公众号“零基础爱学习”一起AI学习。