距离公式:4种证明点到直线的距离公式

将圆与直线的单元放在平面向量之前，进而讨论圆与直线的关係时，特别强调运用圆与直线的联立方程式之解的形态(相等实根、两相异实根，及没有实根) 的「代数判定」方法。儘管此法的使用具有一般性，但计算通常较为繁杂。因此，老师通常还会介绍点到直线的距离公式，利用圆心与直线的距离来判断两者的关係。

然而，此距离公式的介绍常借助向量方法进行证明，使得许多老师倡议将圆与直线与平面向量两个单元互换。不过，仅仅为了一个公式的证明大费周章，并且，更动后也涉及平面上直线的向量表示和直线方程式之间的调整问题。本文中提出几个在99课纲中无须调动次序，也可达到证明点到直线的距离公式之目标的证法。

证法一：(过 P 点作直线 L 的垂线，找垂足 H)

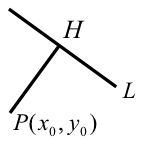
如右图，作 PH¯¯¯¯¯¯¯¯ 垂直 L 于 H，

则直线 PH 方程式为 bx−ay=bx0−ay0

解联立方程式 {ax+by+c=0bx–ay=bx0–ay0，

即得 H(b2x0–aby0–aca2+b2,–abx0+a2y0–bca2+b2)

进而 

此法概念简单，直接硬算，但整体过程不算複杂，可鼓励学生尝试。

证法二：(若 A 为直线 L 上任一点，则 AP¯¯¯¯¯¯¯¯ 的最小值=点 P 到直线 L 的距离)

令 A(x,y) 为直线 L 上任一点，则 ax+by+c=0⇒y=–1b(ax+c)

利用二次函数的性质，当 x=b2x0–aby0–aca2+b2 时，有最小值。

此时，x=b2x0–aby0–aca2+b2

故 

事实上，发生最小值的 A 点即为证法一所求出的垂足 H。利用两点距离的最小值来求点到直线距离的作法具有一般性，也是空间中解决点到直线距离的主要方法。

证法三：(利用三角形面积)

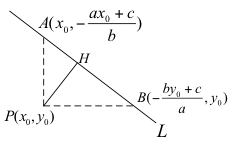
如右图，过点 P(x0,y0) 分别作铅直线和水平线交直线 L

于 A(x0,–ax0+cb)、B(−by0+ca,y0)

ΔAPB的面积=12PA¯¯¯¯¯¯¯¯×PB¯¯¯¯¯¯¯¯=12AB¯¯¯¯¯¯¯¯×PH¯¯¯¯¯¯¯¯

又

PA¯¯¯¯¯¯¯¯=∣∣∣y0–(–ax0+cb)∣∣∣=∣∣∣ax0+by0+cb∣∣∣PB¯¯¯¯¯¯¯¯=∣∣∣x0–(–by0+ca)∣∣∣=∣∣∣ax0+by0+ca∣∣∣AB¯¯¯¯¯¯¯¯=(x0+by0+ca)2+(y0+ax0+cb)2−−−−−−−−−−−−−−−−−−−−−−−−−−−√=a2+b2−−−−−−√∣∣∣ax0+by0+cab∣∣∣

因此，d(P,L)=PH¯¯¯¯¯¯¯¯=PA¯¯¯¯¯¯¯¯×PB¯¯¯¯¯¯¯¯AB¯¯¯¯¯¯¯¯=|ax0+by0+c|a2+b2−−−−−−√

利用三角形面积的高来求距离，也是另一种常见的作法。

证法四：(利用三角函数)

如右图，过点 P(x0,y0) 作水平线交直线 L 于

B(–by0+ca,y0) 且 L 与 x 轴的正向夹角为 θ。

直线 L:ax+by+c=0 的斜率 m=−ab=tanθ

则 sinθ=sin(π−θ)=|a|a2+b2−−−−−−√

则 

此一证法运用学生刚学过的三角函数，也说明了正切函数 (tanθ) 与斜率之间的关係，用来证明点到直线的距离恰到能呼应99课纲的安排，此法最早见于内坜高中林协亿老师写于数学学科中心电子报第60期〈九九课纲中，点到直线距离公式的诠释〉一文。

上述所提四种证法都能避开向量的使用，同时，所运用的证明概念也具有一般性，老师们在介绍点到直线的距离公式时或可一试！