原创 【博客大赛】神奇的电路--------“填谷式”功率因数校正电路方法（转帖）

这种方法是由Spangler于1988年提出的。最近，KitSum采用Spangler电路的倍电压类型的计算机模拟结果表明功率因数有可能达到98％。

       在低功率应用如荧光灯中该低成本解决方案是很有潜力的，原始的Spangler方案已在这方面应用了很多年。它是一个不容忽视的好的、廉价、实用有效的解决方案。

图4.1.7给出了原始的Spangler电路，图4.1.8给出了计算机模拟的该电路输入所期望的电流波形。图4.1.9给出了新型的倍电压类型的Spangler电路，图4.1.10给出了计算机模拟的在倍电压类型电路的输入所期望的电流波形。

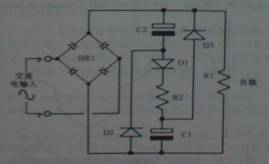4.1.7低功率应用时的“填谷式”功率因数校正电路(Spangler)	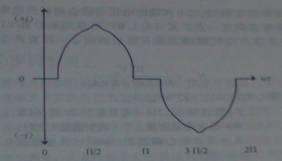图4.1.8  Spangler电路的典型输入电流波形
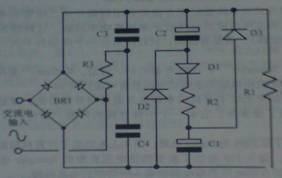4.1.9  改进后的“填谷式”功率因数校正电路(Spangler和KitSum)	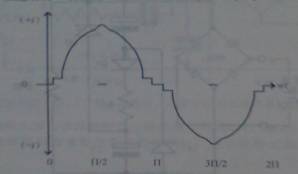4.1.10  改进后的Spangler电路的输入电流的波形

1.3.2功能

       在简单条件下，图4.1.7所示填谷式功率因数校正电路的功能如下：

       考虑输入正弦波为刚过零点的情况。设加在负载R1上的输出电压约为供电输入电压峰值的　　１/3 ，C1通过D3给负载供电，同时C2通过D2给负载供电。因此C1和C2是以并联的方式给负载供电。二极管D1反偏不导通。

因为电源桥式整流器BR1的输出电压超过供电电压，所以桥路二极管被反向配置而输入电流将为零，如图4.1.8中波形的起始部分所示。

当输入电压大于输出电压时，BR1将导通以增大输出电压。此时二极管D2和D3将关断，电容器C1和C2将停止向负载供电。因此负载电路现在直接从电源通过桥式整流器提供，因供电电压小于C1和C2上的电压之和，这时D1将不导通。

直到供电电压达到C1和C2上的电压之和时，加到整流桥输出的负载才是线性的负载，输入电流将和输入电压一样为正弦波形。

当供电电压达到峰值时，它将超过C1和C2上的电压之和，D1通过C2、D1、R2和C1导通并再对串联电容器充电。供电电压峰值附近的短暂电流被电阻器R2限流。

当供电电压开始下降时，所有的二极管都将关断，负载电流又重新直接通过整流桥BR1供电。

当供电电压刚下降到原来峰值的50％时，二极管D3和D2将重新导通，通过并联的C1和C2对负载供电。

这种类型的电路，输出纹波电压将超过半波整流后电压峰值的50％，与电容器的大小无关。因此这种方法仅适用于那些可以承受大的纹波电压的负载。

改进后的电路如图4.1.9所示，小电容C3和C4产生的倍压效应使得在很低的供电电压下依然能够导通，填充了电流波形内的关断部分，如图4.1.10所示，稍微减少了失真。C3和C4比C1和C2小得多。

填谷电路原理如下图，比如220VAC整流滤波后是310V左右的DC，电容串联充电,每个电容器分得的电压大概是155V左右，然后并联放电就也是155V左右；同理90V的AC整流滤波后是130V左右的DC，电容串联充电，每个电容器分得的电压大概是65V左右,然后并联放电就也是65V左右。

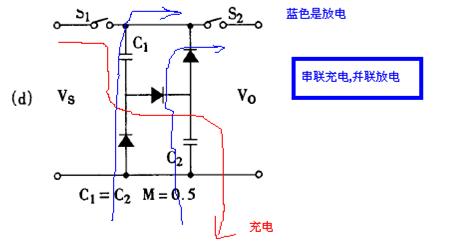
这是一种典型的逐流电路，90年代在照明行业很流行,后来发现这种电路的缺点是供给开关管的直流电压波峰比很高，输出电流波峰比也很高。

填谷电路不适合做降压型电源的。因为填谷电路滤波的电路输出电压谷值只有电解滤波电路谷值的一半。

填谷式的整流方式整流后的输出电压比普通整流后的输出电压低不少，这才是要注意的，有可能用填谷式后在低压输入的时候带载不足。因此可能要加大电感量才能提高到普通整流时的输出功率。

这个电路用于LED照明，谐波测试CLASS D和CLASS B根本就没有办法过，CLASS  C 也过不了。

二极管串联的是10 ohm/0.5W的电阻。改变一下(增大)可能PF会好些，但是，待机会有问题的。

神奇电路的实测结果：

没有加神奇电路前