原创 高速信号回路

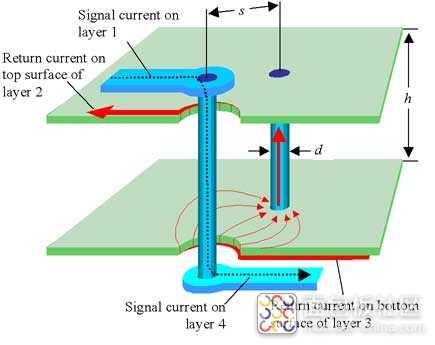
Prior to encountering the via, returning signal current associated with your layer-1 signal trace flows on the top surface of layer 2, right underneath the signal trace on layer 1. The skin depth of copper at high frequencies being much less than the thickness of a typical reference plane, the return current actually flows only on the top surface of solid layer 2; it does not penetrate through that plane.

After traversing the signal via, your signal current appears on a trace located on layer 4. The return current at this point needs to flow on the bottom surface of layer 3 (the nearest surface to layer 4). How does the returning signal current get from layer 2 to layer 3? It can do so through vias IF THE PLANES CARRY THE SAME VOLTAGE, or through bypass capacitors if they do not.

Doesn't the returning signal current just pop between the planes through the parasitic capacitance of the planes themselves, you might ask? A complete answer to that question will have to wait for the next newsletter. The short answer is that in typical cases where the planes are widely spaced (as in a stripline cavity) the current seeks out the nearest metallic connection, such as a via or bypass capacitor, and follows that path.

I brought up the subject of returning signal currents because in order to calculate the inductance of a signal via you absolutely have to know where the returning signal current flows. This need arises because both the signal current and the returning signal current create magnetic fields. Inductance being nothing more than the temporary storage of energy in the form of a magnetic field, both fields must be calculated to determine the total inductance.

Next let's get down to the business of calculating the inductance of a signal via given a known pattern of inter-plane connections.

Assume one signal via and one inter-plane connection via, with the following parameters:

• s - separation between vias, center-to-center
• h - separation between planes 2 and 3 (it doesn't matter if there are other unused reference planes in the way, all that matters is the aggregate spacing between the outermost reference planes traversed by the signal)
• r - radius of the via holes

Inductance is calculated for this configuration by assuming a current of 1 Amp flowing through the signal via and the same 1 Amp returning on the inter-plane connection. From this pattern of currents, one then calculates the magnetic field at all points inside the stripline cavity (between the planes). From this known magnetic field one then integrates, in the region between the vias, the total magnetic flux penetrating through a flat 2-D surface held vertically (like a curtain) and stretched from one via to the other, covering the entire stripline cavity from top to bottom. The total flux penetrating this 2-D surface equals the inductance. The procedure sounds laborious, I know, but it is how inductance calculations are done.

Step 1: The magnetic lines of force due to the signal current form a set of concentric circles centered on the signal via. The field strength is constant in the z-axis direction (parallel to the via). The field falls off with 1/x as you move away from the via, with intensity

Where:

•  is the magnetic permeability of free space, and
• x is the radial distance in meters away from the signal via.

Step 2: The magnetic lines of force due to the return current have the same profile, but centered around the position s of the return-current connection.

Step 3: Integrate the magnetic field between the two vias. This step assumes that the signal and return vias are sufficiently far apart that the existence of each via does not noticeably perturb the magnetic field from the other.

The symmetrical arrangement of the vias suggests that the signal and return vias will contribute equal amounts of flux -- therefore we can just calculate the flux from the signal via and double it to get the result.

This is a two-dimensional integration. The first integration (dx) goes horizontally across the curtain between the two vias. The second integration works vertically from floor to ceiling (z=0 to z=h). Since the field is constant in the z dimension this second integration merely multiplies the first result by a factor of h.

As the integrand in this expression involves 1/x, the integrated result involves logarithms. The inductance represented by the combination of one signal via and one return via at distance s equals:

In metric mks units (h, s, and r in meters, L in Henries), the constant μ/2π works out to 2·10-7 H/m (assuming a non-magnetic dielectric). In English units, (h, s, and r in inches, L in nH) the constant μ/2π equals 5.08 nH/in.

Other examples are worked similarly. If the return current is carried mainly on two vias equally spaced on either side of the signal via, where the spacing from signal via to either return via is s and the via radius is r:

[two-vias]

If the return current is carried mainly on four vias equally spaced in a square pattern on four sides of the signal via, where the spacing from signal via to any return via is s and the via radius is r:

[four-vias]

If the return current is carried mainly on a coaxial return path completely encircling the signal via, where the spacing from signal via to the return path is s and the via radius is r:

[coax]

The last formula I hope you will recognize as the inductance of a short section of coaxial cable with length H and outer diameter 2s. I hope this recognition will lend credence to the idea that the position of the returning current path is an important variable in the problem.

Formula [7.9], page 259 in High-Speed Digital Design, lists the inductance of a via as:

[7.9]

This formula for L? is a gross approximation that glosses over the position of the returning current path, a simplification I greatly regret not making more clear in the book. It makes the crude assumption that the return path is approximately coaxial and located at a distance s=2eh, where e is the base used for natural logarithms. When the inductance really matters, a more accurate approximation is needed.

To see how formula [7.9] was derived, substitute 2r for the diameter d, and incorporate the additive factor of 1 inside the logarithm as a multiplicative factor of e:

Comparing this to the formula [coax] shows the unwritten assumption present within formula [7.9], namely that the return path is coaxial and located at a distance of approximately s=2eh away from the signal via.

If you are working with a 0.063-in. thick board with eight-to-ten layers, the outer two solid planes are probably about 0.050 in. apart. This height times 2e would be .2718 in.  If you have a bunch of return paths about this far away, that is the case approximation [7.9] was intended to cover.

If you hold the position of the return paths constant and vary the inter-plane separation, the inductance changes linearly with inter-plane height (which equates roughly to via length).

If you modulate the position of the return paths at the same time you vary the inter-plane height, always keeping s=2eh, you get formula [7.9].

Note that all the approximations I have provided so far have the property that they give you the inductance of a via and its associated return path only covering that part of the via embedded between the planes. The part of the via that sticks up above the planes is not included. If you want to model that part (and I think that at today's speeds we are beginning to *need* that part), check out the models in my article: "Parasitic Inductance of Bypass Capacitors."