原创 基于CCD激光衍射暗纹间距的精确测量算法研究

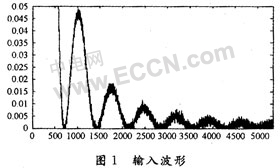
由于噪声的多样性，本系统采用LMS(最小均方)自适应滤波。LMS算法用于自适应地调节一个FIR滤波器的系数。x(n)是已知输入序列，期望序列是d(n)，步长△和期望的自适应FIR滤波长度为N，相应的输出序列是y(n)，FIR滤波器可调节的系数h(k)，M是输入序列的长度。

将期望序列与FIR滤波器的输出做比较，然后取d(n)与y(n)之差形成误差序列e(n)：

并选择这个FIR滤波器的系数使平方误差最小。用任意选择的h(k)作为开始，然后将每一新的输入样本x(n)输入到这个自适应FIR滤波器，计算相应的输出y(n)，形成误差信号e(n)=d(n)-y(n)，并按方程：

更新滤波器系数，x(n-k)是输入信号在时间n位于滤波器第k个抽头上的样本，而e(n)x(n-k)是对第k个滤波器系数的一个梯度负值的估计。这就是为自适应地调节滤波器系数而使平方误差和达到最小的LMS递推算法。

通过自适应滤波，信噪比增大，使CCD输出信号更适合于精确处理。滤波后的CCD信号如图2所示。

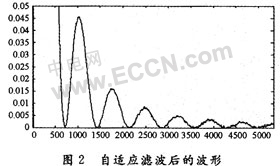
2 粗略暗点的提取

判断暗点用扫描法，当扫描过程中满足以下4个条件时可视为暗点：

(1)I(i)<I(i+1)，即该位置的光强小于他后一个位置的光强；

(2)I(i)<I(i-1)，即该位置的光强小于他前一个位置的光强；

(3)该位置的光强小于他周围光强平均值的0.2～0.5倍；

(4)该位置不处在开头或者结尾。

但是在实际中，这是因为噪声太大或者其他外界因素的影响，此方法有可能造成暗点识别失败。因此用上述方法找到的暗点只能在准确暗点的周围摆动，如图3所示。

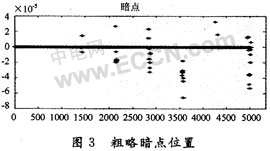
设“暗点”位置函数为U(i)，i=1，…，L，其中L是图2中暗点的个数。

第三步：对其求和取平均。例如：index(1)=4，那么从U(1)到U(4)相加除以4即为第一个暗点的粗略位置，index(2)=9，就从U(5)加到U(9)，用和除以5，得出的值便是第二个暗点的粗略位置。

通过以上算法之后，得到的暗点粗略位置如图4所示。

3 精确暗点的提取

由粗略暗点左右取若干多个点，利用最小二乘法进行曲线拟合。取上述条纹中心的粗略位置两侧各1／4波形周期的数据进行拟合。其模型为：

对所拟合的曲线取倒数，并令其为零，即求出了暗点的精确位置。

图5是对其中一点进行拟合的效果。

精确暗点位置为718.6。

4 实验结果

本实验所采用的TCD1500C线阵CCD进行光电转换，分别采用原始的方法和本文所提到的处理方法对标称值为202 μm细丝进行测量，测量结果如表1所示。

5 结 语

本文在激光衍射法测量微细线径的基础上，提出了用自适应滤波法对CCD图像进行滤波，并用4个暗点判定条件进行判定，找到了粗略暗点位置。在粗略暗点的基础上用差分法以及取平均的方法对粗略暗点进一步精确定位。最后对所找到的粗略暗点用最小二乘局部曲线拟合的方法找到暗点的精确位置。通过实验，得知用改进方法比用传统方法的测量精度高，而且可重复性好，完全可用于实际测量。