


欧拉公式是根据其提出者莱昂哈德·欧拉(??????Leonhard Euler)而命名的公式。
(1) 在複分析领域的欧拉公式为:
 ,存在:
,存在: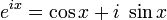
 时,欧拉公式的特殊形式为?
时,欧拉公式的特殊形式为?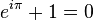 ?。 (参见欧拉恒等式)
?。 (参见欧拉恒等式)複分析领域:
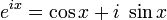 ,?
,?
 ,?
,? ?和?
?和? ?写成泰勒级数形式:
?写成泰勒级数形式:


 代入可得:
代入可得:
定義函數

由於

可知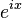 不可能為0,因此以上定義成立。
不可能為0,因此以上定義成立。
則 之微分為:
之微分為:
 }-
}-因此 必須為一常數函數。
必須為一常數函數。
所以:

重新整理,即可得到:

這公式可以說明當x為實數時,函數?eix?可在?複數平面描述一單位圓?。且x為此平面上一條連至原點的線與正實數軸的交角(順時鍾的)。 先前一個在複數平面的複點只能用卡式坐標系描述,尤拉公式在此提供複點至極坐標的變換
任何複數?z?=?x?+?iy?皆可記為


在此
 /5
/5 
文章评论(0条评论)
登录后参与讨论