作者:Pete Semig和Collin Wells,德州仪器 (TI)
本系列文章将介绍电流检测相关内容,阅读之后,您会牢固掌握电流检测的许多基础知识,了解电流检测所使用的一些器件,知道如何计算某种解决方案的精确度以及印制电路板 (PCB) 布局和问题检修的一些指导原则。本文将为您详细介绍影响某种解决方案精确度的一些规范。这些规范包括输入补偿电压 (Vos)、共模抑制比 (CMRR) 和电源抑制比 (PSRR)。
精确度
分流器测量的系统精确度会受到许多误差源的影响,其中一些如表1 所示。方程式1 表明了极端系统精确度情况。
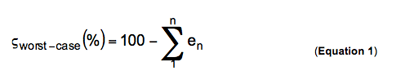
其中,Sworst-case (%) 为每个误差源的误差贡献度。但是,一种更为实际的系统精确度计算方法是,将无关联误差写成一个和的平方根 (RSS),如方程式2 所示。


由于表1 所列大部分误差均为输入参考 (RTI),因此我们最好是就输入方面来对精确度进行讨论。参考器件输入的误差乘以器件增益,得到其对输出的影响程度。
输入补偿电压
输入补偿电压一般为影响某种解决方案精确度的最大因素。它的定义是“一个必须施加于输入端之间以强制静态DC 输出电压为零或者其他规定电平的DC 电压”。[1]放大器的理想Vos 为0V。但是,工艺差异和器件设计限制等原因,会导致Vos 不为零。
所有输入参考误差均根据理想分流器电压计算得到。理想分流器电压应为负载电流和理想电阻器值的乘积。系统中,标称负载电流为5A,理想关联电阻器值为1mΩ,则器件Vos 规范的误差贡献程度计算方法如方程式3 所示。假设我们决定使用INA170,其最大Vos 规范为1mV。
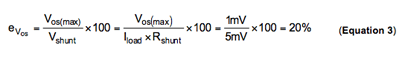
要想减小这种误差,我们有两种方法:增加Rshunt 电阻,或者降低Vos (max)。增加Rshunt 电阻方法是否可行,取决于成本、电路板空间或者功耗情况。另外,我们也可以尝试找到一种具有更低Vos 的替代器件。
最后,需要注意的是,负载电流与误差成反比关系。在我们的例子中,标称负载电流为5A 时,计算得20%。如果系统负载电流减少,则Vos 规范产生的有效误差增加。因此,设计人员应在最小负载电流下计算极端误差。
共模抑制比
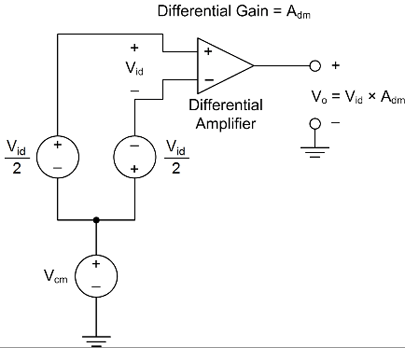
在介绍CMRR 以前,我们需要重新复习一下输入共模电压知识。本系列文章的第一篇便对此进行了讨论,放大器的输入共模电压为两个输入端的共用平均电压。尽管这样说确实没有错,但最好还是将分流器电压同共模电压区分开来。通过定义Vid(差动输入电压),可以达到这个目标。在电流检测应用中,它还可以被看作是分流器电压。图1显示了输入共模电压的另一种定义,其使用了差动输入电压。图1还再次提出了差模增益 (Adm) 的概念。差动放大器的理想输出为差动输入电压和差模增益的乘积。
图1共模电压另一种定义[2]
CMRR 可影响电流检测解决方案的精确度。它是器件共模信号抑制能力的度量标准。这很重要,因为共模信号会以差动信号的形式出现在器件中,从而降低解决方案的精确度。
CMRR 通常在产品产品说明书中以线性刻度 (µV/V) 或者对数刻度 (dB) 单位表明。如果单位是dB,则极端值为最小值。如果单位为µV/V,则极端值为最大值。
要想计算器件CMRR 规范产生的误差,我们需要:产品说明书列出的极端CMRR规范、产品说明书规范表的共模电压测试条件(Vcm-pds)以及系统的共模电压(Vcm-sys)。
例如,假设系统共模电压为50V (Vcm-sys),并且分流器电压标称为5mV。我们使用INA170 计算误差,其极端CMRR 规范为100dB (min),Vcm-pds=12V。
由于规范单位为dB,我们需要将其转换为线性刻度,如方程式4 所示。
现在,我们来计算误差,如方程式5 所示。
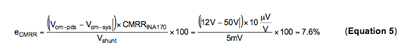
想要降低CMRR 带来的误差贡献值,我们有两种方法:增加分流器电压,或者选择一个拥有更好CMRR 性能的器件。改变Vcm-sys 通常并非为一种可行的方法,因为具体应用决定了它的大小。
这样处理CMRR 的目的是,让读者能够迅速和有效地理解其如何影响测量的精确度[1, 3, 4]。
电源抑制比
PSRR 是电源电压变化引起Vos 变化程度的一种测量方法。PSRR 所产生误差的计算方法与CMRR 类似。
要想计算器件PSRR 规范所产生的误差,我们需要:产品说明书的极端PSRR规范、产品说明书规范表的电源电压测试条件 (Vs-pds) 以及在系统中为器件供电的电源电压 (Vs-sys)。
例如,INA170 的极端PSRR 规范为10µV/V(最大),且Vs-pds=5V。如果器件实际电源电压为30V (Vs-sys),则PSRR所产生的误差可以利用方程式6 计算得到。就前面的几个例子而言,我们假设分流器电压为5mV。
要想降低PSRR 带来的误差贡献值,我们有两种方法可以使用:增加分流器电压,或者选择一个PSRR 性能更高的器件。改变Vcm-sys 通常并非为一种可行的方法,因为具体应用决定了它的大小。
本例中,PSRR 单位已经指定为µV/V。如果该值单位指定为dB,则在使用方程式6 以前必须将其转换为线性刻度。
其他误差
一些规范,例如:增益误差和分流电阻器容差等,通常会以百分比的形式出现。这使得精确度计算更加简单。
表1 还列出了Vos 漂移和变化。输入补偿电压漂移可测量温度变化带来的Vos 变化。这种规范一般为:
但是,输入补偿电压变化则并不那么简单。输入补偿电压变化测量的是时间变化带来的Vos 变化情况。我们通常可以在产品说明书中看到这种规范,并且其仅为估计值。准确估计这种变化的一种方法是,知道10 年内器件Vos 的变化,不会大于器件的最大Vos 规范。这种变化是器件初始Vos 规范之外的变化。
综合计算
如前所述,综合误差的各个方面,便可知道系统的总体精度。只需将每一项相加,便得到极端误差,而以RSS 方式将它们结合起来就得到一个更加准确的结果。
就本文所列举的Vos、CMRR 和PSRR 例子而言,极端精确度为67.4%,如方程式7 所示。
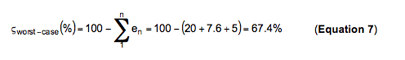
使用RSS 方式综合各个误差,得到更准确的精确度为78.03%,如方程式8 所示。
总结
本文介绍了电流检测精确度概念,它与Vos、CMRR 和PSRR 等规范有关。文中所举例子,说明了在某个具体应用中如何计算这些规范所产生的误差。另外,我们还简单介绍了如增益误差、分流器容差和Vos 漂移与变化等其他误差。本系列文章的最后一篇将讨论电流检测PCB 布局和问题检修指导原则。
参考文献
1、《如何理解运算放大器的各种规范》,作者:Karki,刊发于1998 年 TI《白皮书:SLOA011》
2、《运算放大器:设计与应用》,作者:Tobey, Graeme, Huelsman,刊发于1971年《McGraw-Hill》
3、《运算放大器与模拟集成电路设计》,作者Franco,刊发于2001年《McGraw-Hill》第3 版。
4、《简单运算放大器:基础到实际应用》,作者:Frederiksen,刊发于1988年《McGraw-Hill》修订版。
作者简介
Peter Semig 现任 TI 高精度线性产品部应用工程师,主要负责差动放大器、仪表放大器和分流监视器的技术支持。Peter 毕业于密歇根州立大学(东兰辛)(Michigan State University, East Lansing, Michigan),获电子工程理学士学位和硕士学位。如果您对本文有疑问,请发送电子邮件至ti_petersemig@list.ti.com。
Collin Wells现任 TI 高精度线性产品部应用工程师,主要负责工业产品和应用的技术支持。Collin 毕业美国得克萨斯大学达拉斯分校 (University of Texas, Dallas, Texas),获电子工程理学士学位。



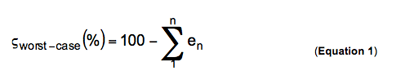


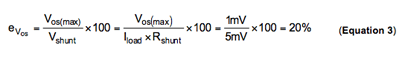
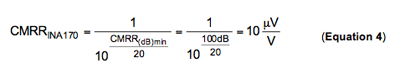
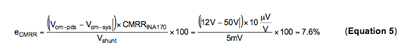
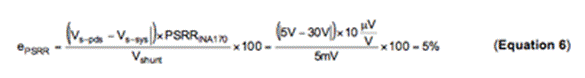

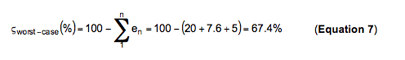
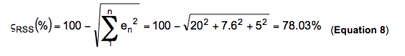
 /2
/2 
文章评论(0条评论)
登录后参与讨论