原创 【TI博客大赛】基于MSP430F449的音频功放-3

四、理论分析与计算

1. PWM调制电路分析与计算

三角波调制法是建立在相等时间间隔内的能量等效于正弦波所包含能量概念上的一种脉宽调制技术，其等效示意图如图:

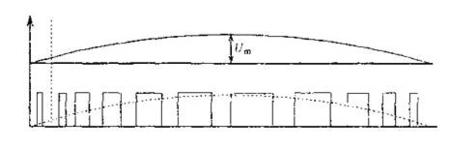
图9 PWM等效示意图

正弦波的一个周期被等分成N（N为偶数）等份，则每等份脉宽为，从而可分别计算出各时间间隔内正弦波所包含的面积，在每个特定时间间隔内，据可用一个脉宽与之对应的正弦波所包含的面积相等或成比例，脉冲幅度一定的矩形电压脉冲来代替相应的正弦波部分。这样N个脉宽不等的脉冲即组成一个与正弦波等效的脉宽调制波形。设正弦波幅度为，等效矩形波形幅度则为，则各等效矩形脉冲波的宽度为

式中                         ，

为各等效脉冲的位置中心角，表明又有能量等效出的脉冲宽度与分段中心角的正弦值成正比。

设三角波频率与正弦波的频率之比即载波比为N，则可得，由图可看出与相似，所以有。由于

；（三角波的幅值）；

令脉宽，则。

    当N较大时有，将带入可得:

由上式可知：当载波比固定且较大时，通过比较器输出端的矩形脉冲宽度正比与正弦波的幅值与三角波幅值之比，也正比与分段中心角。对于脉宽调制波形，其基波与各次谐波幅值表达式为

由上式可知：基波的幅值与各次谐波的幅值与脉冲宽度有关，而脉冲宽度由于幅度之比有关。

图为谐波幅值与基波幅值之比与幅度比的关系曲线。又该曲线可知：正弦波的幅度小于三角波幅值时，比较其输出电压基波分量几乎是与调制波比值呈线性关系。有：。

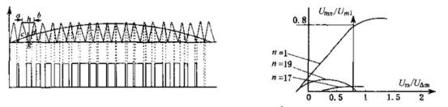
图10谐波幅值与基波幅值之比与幅度比的关系曲线

2音调控制电路理论分析

音调控制电路结构如下图：

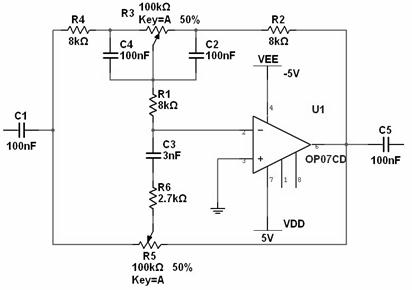
图11 音调控制电路

设电容，在中、低频区时C3可视为开路，在中、高频区C4、C2可视为短路。

（1）  当时，当滑线变阻器R3在最左端时对应于低频提升的最大值，R3在最右端对应于低频衰减最大情况。如图a、b值所示，图a所示为一阶有源低通滤波器有，.

当时，C2视为开路，运放反相端虚地则此时电压增益为：；

当时，由于则有；

当时，则有，此时电压增益相对于下降17dB。

同理可得b所对应的电路增益表达式。

（2）  当时，此时将C4、C2视为短路。当滑线变阻器R5在最左边时，对应高频提升最大情况；R5在最右边时对应于高频衰减最大情况图a为一阶低通滤波器，对应，。

当时，C3视为开路此时电压增益;

当时，；当时，；

当时，则有。

同理可得出图b所示电路表达式