


这里的“特性”是指电机结构(非电路)方面的特性、电路的各种工作和电机输出(转速、转矩)。所要介绍的特性也是在开发无刷电机和讨论相关内容时,大家都知道、并认为是理所当然的事情、经常提到的内容。这些都是电机驱动器的开发人员应该装入大脑知识宝库中的内容,需要认真对待。
实际的电机驱动信号波形也有一些是在设计图(即时序图)中无法体现的。接下来将为您介绍其中无法通过此前的介绍内容理解的一些关键要点。
请注意,上述标题中的编号对应后文所述要点中的编号。
首先,我们从驱动无刷电机的实际信号中选取了一些在以往的介绍中无法简单讲明白的要点进行介绍。
无刷电机驱动的实际信号波形
通常需要使用示波器来观察电机电气方面的表现。示波器可以监测电路的电压值或电流值。我们用示波器来尝试监测基于下面电路图的电路板上的信号,可以看到在示波器显示屏上出现了下图所示的波形。

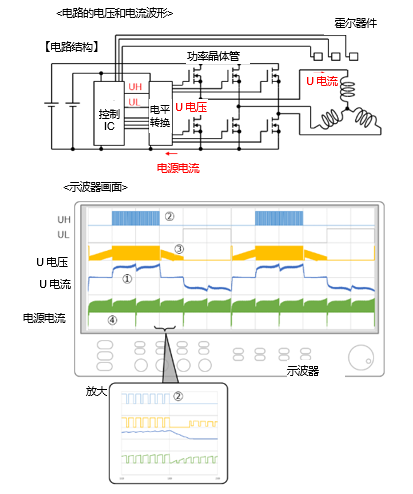
这些是电机驱动中常见的信号波形,从上到下依次是U相的高边栅极信号(UH)、低边栅极信号(UL)、U相绕组引脚电压、U相绕组电流和电源电流。这些波形的特点仅靠此前“时序图”中的知识是无法讲明白、无法理解的。在实际运行电机时,会生发出很多疑问,比如“为什么会这样?
下面按顺序列举了几点,这几点应该都是无法通过此前的内容理解的。编号与上图“示波器画面”中显示的编号一致。
对于驱动电机和了解电机特性而言,这些都涉及到非常重要的项目,因此在接下来的文章中我们将依次进行介绍。
我们先来了解一下①U电流:
“U电流”是绕组电流。要了解该波形,首先需要了解绕组电流和感应电压
前面我们已经对无刷电机实际信号波形中的疑问①“U电流为什么会呈现这样的波形”进行了解释说明。本文将总结说明绕组电流与感应电压之间的关系。
与无刷电机的感应电压波形息息相关的绕组电流
在此前相关解说的基础上,我们再次来探讨一下绕组电流波形。
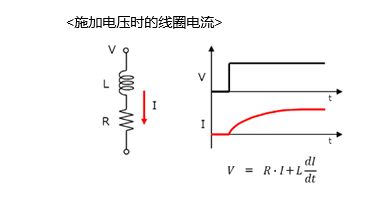
考虑到无刷电机的线圈会产生感应电压,所以在“无刷电机的绕组电流”所示的等效电路图中增加了感应电压(Vbemf)。这样的话,如果是下图所示的施加电压和感应电压波形,则实际施加于线圈的电压将是图中灰色部分的电压。
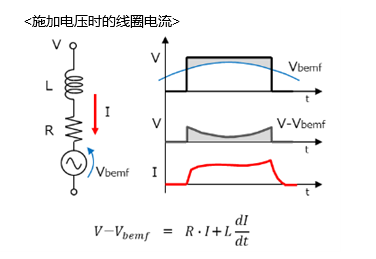
从上图中可以看出,实际施加在该绕组线圈上的电压开始时很大,中间变小,然后又变大。由于电压波形(灰色部分)的形状如此,所以绕组电流就是中间凹陷状的波形(与“无刷电机的绕组电流”中所示的波形相同)。
讲到这里,您的脑中是不是浮现出了“如果施加电压和感应电压的大小发生变化,那么绕组电流的大小及其波形也会随之变化”呢?施加电压是控制IC可以控制的电压,而感应电压则会因各种条件而变化。就如此前曾经介绍过的,感应电压是通过线圈的磁通量的变化量,因此关于感应电压的大小(峰值),可以说:
▶磁体的磁力越大感应电压越大 ← 因为磁通量的绝对量增加
▶线圈的匝数越多感应电压越大 ← 因为发电的线圈量增加
▶电机的转速越快(越高)感应电压越大 ← 因为磁通量的变化变快。反之则越小
在这里就不再赘述严谨的理论了,需要知道的是,感应电压的大小在这样的条件下会发生变化。
下图给出了当感应电压的大小发生变化时,电流波形的变化示例。当感应电压越大且接近施加电压的大小时,电流中央的凹陷程度将会更明显(下图上侧)。另外,在施加电压的时间点电流波形也会发生变化,该变化与感应电压的大小无关(下图下侧)。
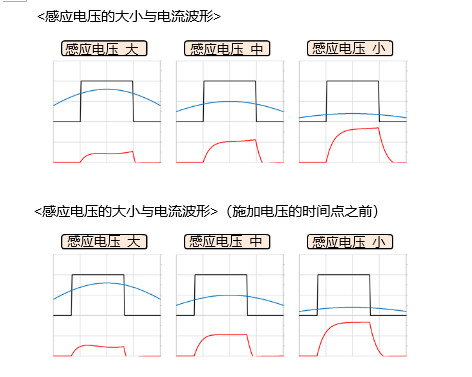
这是以120度激励(矩形)为例的波形变化情况,当然,在其他的激励模式下,绕组电流也会因感应电压的大小、位置以及形状而变化。这会对电机的特性产生各种影响,后续我们会探讨相关的内容。
关于疑问①“U电流为什么会呈现这样的波形”的主要原因——绕组电流和感应电压相关的解说就到这里。下一篇将探讨②“UH的信号呈脉冲状”。
我们已经通过无刷电机驱动实际信号波形解决了第一个疑问——①的U电流。
“U电流”是绕组电流。要了解该波形,首先需要了解绕组电流和感应电压。
无刷电机的绕组电流
流过电机绕组的电流是决定绕组磁场大小、乃至转矩大小的重要因素。因此,我们需要充分理解电流是如何决定这些参数的。本文将使用“无刷电机时序图的绘制方法”中给出的120度激励电流波形进行解说。
120度激励的电流将以360度的电角度(1个电周期)切换6次。具体而言,比如在下图中,从U相流向V相的电流体现为“从U相切换为W相”,这样的动作执行6次。
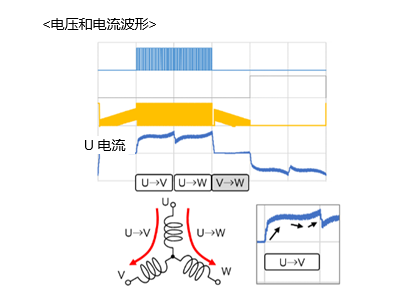
在这样的切换过程中,流动的电流会暂时下降后再恢复。另外,当电流在其他相流动时(例如电流从V相流向W相时的U相),U相电流不会流动,因此电流值会变为零。在负电流侧也是如此。
这就是120度激励的电流波形会呈现图中所示波形的一个原因,不过还有一部分是用这个原因解释不了的。例如,在图中的“U⇒V”范围内,曾经变大的电流在短暂减小后再次变大。为什么会出现这样的波形呢?
为了便于解说,我们先来温习一下线圈电流相关的理论知识。理想的线圈是用电感来表示的,但实际上里面含有有电阻值,因此在电路中可用下图的形式来体现。在这个电路中,当施加了电压时,电流波形应该是如图所示的波形,电流不会短暂减少。
实际上,可以说形成这种增减状态的电流波形的主要原因,正是使无刷电机的控制难度增加的因素之一。其主要原因是线圈的发电。
此前我们也提到过,电机是将电能转换为机械能的一种设备,对于使用永磁体的电机而言,只要利用外力使之旋转就可以将机械能转换为电能,也就是所谓的“发电机”。而且,这种发电现象不仅发生在借助外力旋转时,其实也发生在“自转时”。这种由永磁体和线圈产生的发电电压被称为“感应电动势”、“反电动势”、“感应电压等,有时也被表述为“BEMF(ack electromotive force)”。在这里我们将其称为“感应电压”。
这种感应电压是绕组电流增减的主要原因。
无刷电机感应电压产生的原理
无刷电机是通过转子转动而在线圈(绕组)上产生感应电压的。这种感应电压会对电机的特性产生不同程度的影响,因此与“绕组电流”一样,我们也需要了解这种感应电压。
首先,请回忆一下在学校物理等课程中学过的“电磁感应”。线圈试图阻止磁场(磁通量)发生变化。例如,如下图所示,随着N接近线圈,通过线圈的磁通量会逐渐增加,因此线圈电流沿着产生与之排斥的磁场的方向流动。该电流使得线圈两端产生电压。相反,随着N远离线圈,线圈试图维持磁场的方向,因此在靠近时会产生反向的电流和电压。这种产生电压的现象叫做“电磁感应”。此时的电流被称为“感应电流”,电压除了这里使用的“感应电压”外,还被称为“感应电动势”、“反电动势”等。
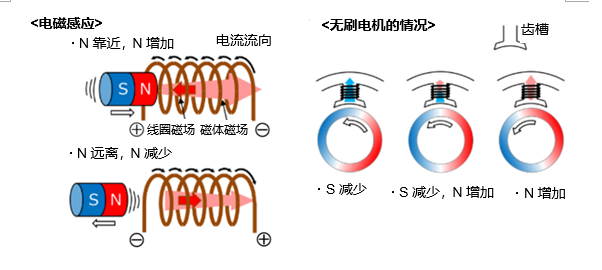
*图中磁体磁场的箭头表示磁场大小的变化。实际上线圈内并不会发生像图中那样大小的不均匀。
对于无刷电机而言,与其说磁体靠近或远离,不如说通过线圈的磁通量会因转子的旋转而变化,因而产生与其变化量相应的感应电压(上图右侧)。
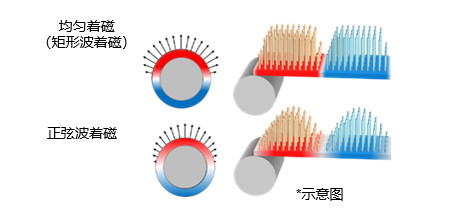
在考虑通过线圈(齿槽)的磁通量变化量时,需要知道“在不同的位置转子表面的磁通量大小不同”这一点。有的转子磁通密度基本均匀,也有的转子如下图所示,磁通密度大小在圆周方向呈正弦波状分布。后者这种转子有“正弦波着磁转子”等称呼。在这种着磁的情况下,当转子旋转时,就会发生如上图右侧所示的磁通量变化。
无刷电机的感应电压波形
无刷电机的感应电压是通过线圈的磁通量变化作为电压体现出来了。这里所说的“通过线圈的磁通量”是指进入绕线齿槽的磁通量。
我们先来谈谈这个“进入齿槽的磁通量”。电机磁体和线圈的位置关系如下图所示。也就是说,可以认为每个齿槽中会通过与该齿槽相对的磁体的磁通量。
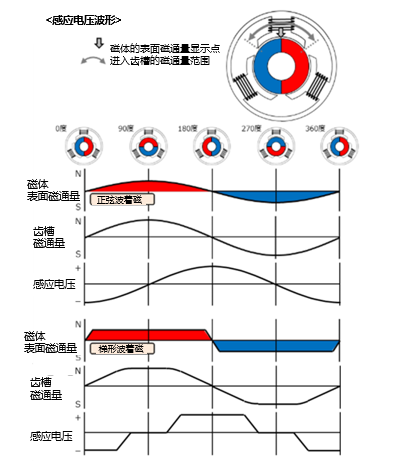
接下来我们以图中所示的表面磁通量(两种模式)为例,来思考进入齿槽的磁通量。
该图用转子旋转一圈(360度)的细分图来表示图上方的结构图所示的“表面磁通量显示点”的位置对面的转子表面磁通量的大小。另外,还计算了进入齿槽的总磁通量,同样是按照360度计算的。该总磁通量是通过将齿槽相对的磁体的磁通量(图中的“进入齿槽的磁通量范围”)相加计算得出的。也就是说,当转子旋转、位置改变时,磁通量就会发生变化。
例如,在0度的转子位置上,齿槽对面的磁极由于N和S等量,因此齿槽磁通量为零;在90度的位置上,与N的中心相对,因此齿槽磁通量最大。如果按360度计算,那么在正弦波着磁的情况下,齿槽磁通量(总磁通量)也是正弦波的。
而且,这种齿槽磁通量的变化(微分)会成为感应电压(微分时符号要加负号)。也就是可以理解为,相位与对面的表面磁通相差90度。
着磁波形大致可以分为正弦波、矩形波和梯形波。第二个例子是梯形波着磁的情况。顺便提一下,前面提到的矩形波与这里的梯形波的区别在于N和S的切换梯度,但并没有明确的定义。通常把坡度比较平缓的称为“梯形波”。
在梯形波的情况下,进入齿槽的磁通量波形不再是正弦波波形。用微分计算得出的感应电压波形也是图中所示的形状。关于梯形波着磁的感应电压,应该注意的是着磁波形与感应电压波形的特点存在明显不同。例如,梯形波着磁尽管表面磁通的N和S变化部分的斜率比正弦波着磁更陡峭,但其感应电压的正负变化部分(过零点)要比正弦波着磁更平缓。
感应电压波形的不同会影响各种电机特性和控制特性(后续会具体介绍)。然而,由于不同类型电机的感应电压形状也各不相同,而且与着磁波形也不一致(正弦波除外),因此很难把握。作为电机控制的第一步,要有意识地确认要控制的电机的感应电压波形是什么样的波形,这一点非常重要。
来源:techclass.rohm
 /4
/4 
文章评论(0条评论)
登录后参与讨论