本文简要回顾了傅里叶理论,尤其是 FFT 。本文还介绍了一些典型应用,并提供了有关如何充分利用 Keysight 示波器的 FFT 功能的一些提示。
傅里叶理论
通常,当使用示波器测量信号时,它会在时域中查看(图 1a)。也就是说,垂直轴是电压,水平轴是时间。对于许多信号,这是查看它们的最合乎逻辑和直观的方式。但是当对信号的频率内容感兴趣时,在频域中查看信号是有意义的。在频域中,垂直轴仍然是电压,但水平轴是频率(图 1b)。频域显示显示每个频率上存在多少信号能量。对于正弦波等简单信号,频域表示通常不会向我们显示太多额外信息。然而,对于更复杂的信号,时域中的频率内容很难发现,而频域可以提供更有用的信号视图。

图 1
(a) 以时间函数显示的信号。
(b) 以频率函数显示的信号。
傅里叶理论(包括傅里叶级数和傅里叶变换)在数学上将时域和频域联系起来。傅里叶变换由以下公式给出:
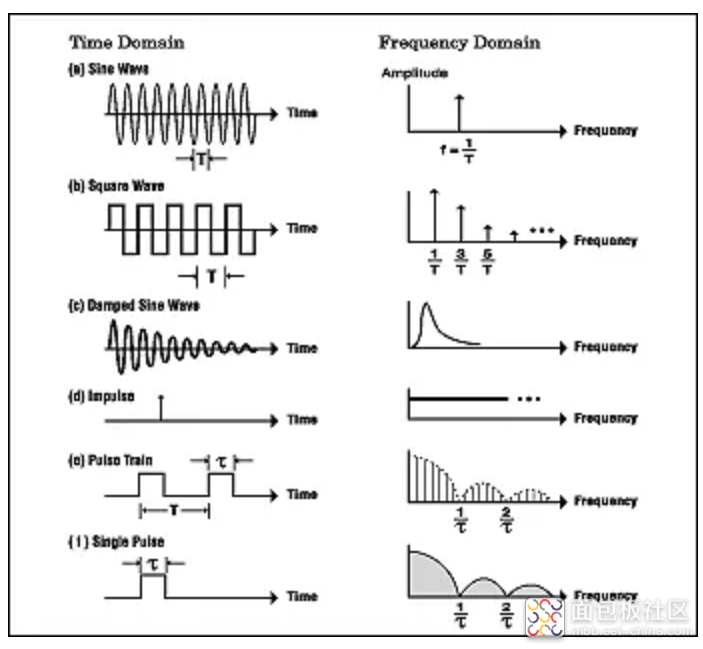
我们不会在这里详细讨论数学,因为有许多书籍广泛介绍了该理论(请参阅参考资料)。图 2 显示了一些在时域和频域中表示的典型信号。
图 2:频谱示例
快速傅立叶变换傅立叶变换的离散(或数字化)版本称为离散傅立叶变换 (DFT)。此变换采用数字化时域数据并计算频域表示。虽然常规傅立叶理论有助于理解时域和频域之间的关系,但 DFT 允许我们计算真实世界时域信号的频域表示。这使傅立叶理论的强大功能脱离了数学分析的世界,进入了实际测量领域。带有测量/存储模块的 Keysight 示波器使用一种称为快速傅立叶变换 (FFT) 的特殊算法来计算 DFT。FFT 和 DFT 产生相同的结果,该功能通常简称为 FFT。
Keysight 系列示波器通常将时域波形数字化并将其存储为 4000 点记录。FFT 功能使用其中的 1000 个点(每四个点)来生成 500 点频域显示。此频域显示的频率范围从 0 到 feff /2,其中 feff 是时间记录的有效采样率(图 3a)。
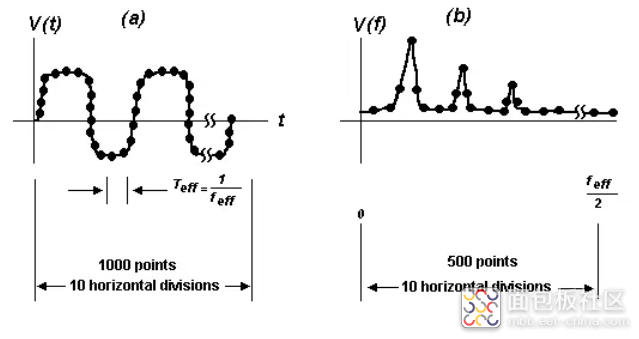
图 3
(a) 采样的时域波形。
(b) 使用 FFT 得到的频域图。
有效采样率是样本间时间的倒数,取决于示波器的时间/格设置。对于 Keysight 系列示波器,有效采样率由以下公式给出:
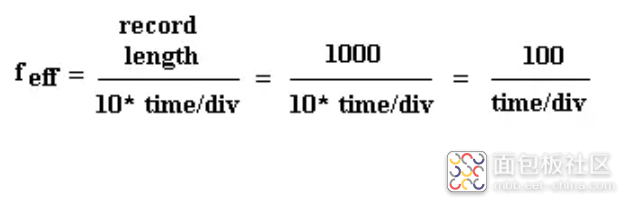
因此,对于任何特定的时间/格设置,FFT 都会产生从 0 到 feff /2 的频域表示(图 3b)。当 FFT 功能处于活动状态时,转动时间/格旋钮或按下 ± 键时会显示有效采样率。请注意,FFT 的有效采样率可能远高于示波器的最大采样率。示波器的最大采样率为 20 MHz,但随机重复采样技术可以如此精确地及时采样,以至于 FFT 看到的采样率可以高达 20 GHz。
默认频域显示涵盖 0 到 feff /2 的正常频率范围。中心频率和频率跨度控件可用于放大 FFT 基本 0 到 feff /2 范围内较窄的频率跨度。这些控件不会影响 FFT 计算,而是导致频域点以扩展形式重新绘制。
混叠频率 feff /2 也称为折叠频率。通常出现在 feff /2 以上(因此超出了 FFT 的有用范围)的频率会折叠回频域显示中。这些不需要的频率分量称为混叠,因为它们错误地出现在另一个频率的混叠下。如果有效采样率大于被测信号带宽的两倍,则可以避免混叠。
三角波的频率内容包括基频和大量奇次谐波,每个谐波的幅度都小于前一个谐波。在图 4a 中,在时域和频域中显示了一个 26 kHz 三角波。图 4b 仅显示频域表示。最左边的大谱线是基频。下一个重要谱线是第三谐波。下一个重要谱线是第五谐波,依此类推。请注意,较高的谐波幅度较小,第 17 次谐波刚好在 FFT 噪声基底上方可见。第 17 个谐波的频率为 17 x 26 kHz = 442 kHz,在图 4b 中位于折叠频率 feff /2(500 kSa/秒)内。因此,没有发生明显的混叠。
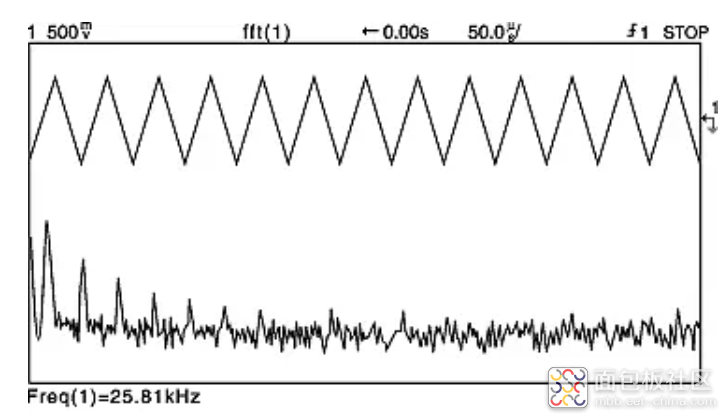
图 4a:26kHz 三角波的时域和频域显示。
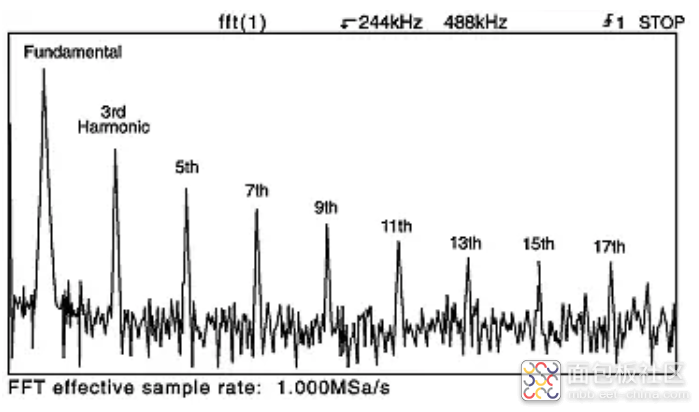
图 4b:三角波的频谱。

图 4c:在较低的有效采样率下,上部谐波显示为混叠。
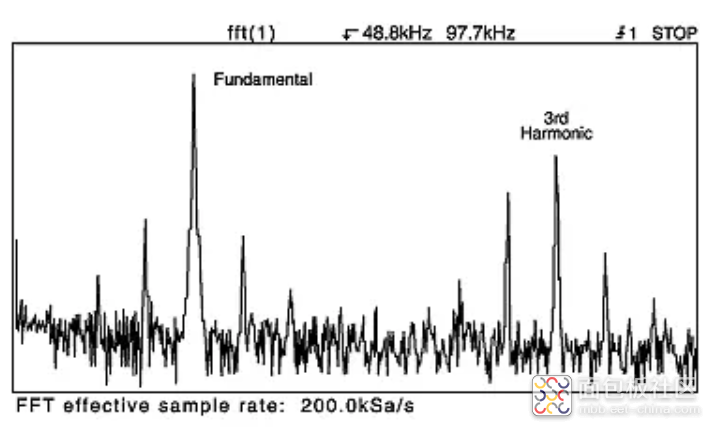
图 4d:在更低的有效采样率下,只有基波和第三谐波没有混叠。
图 4c 显示了相同波形的 FFT,其中时间/格控制向左旋转一次,导致有效采样率为 500 kSa/秒,折叠频率为 250 kSa/秒。现在,三角波的上部谐波超过了折叠频率,并在显示屏中显示为混叠。图 4d 显示了相同三角波的 FFT,但有效采样率(200 kSa/秒)和折叠频率(100 kSa/秒)更低。此频率图混叠严重。
混叠的影响通常很明显,特别是如果用户对信号的频率内容有所了解。频谱线可能出现在没有频率成分的地方。当低级混叠频率出现在测量的本底噪声附近时,混叠的影响会更加微妙。在这种情况下,由于混叠在频域中略有不同,基线可能会在每次采集之间反弹。
混叠频率成分可能会产生误导,并且在测量中是不可取的。通过确保有效采样率足够高,可以查看带宽受限的信号(即没有高于某个频率的频率成分)。通过选择快速时间/分度设置,有效采样率可以保持在尽可能高的高度。虽然快速时间/格设置可产生高有效采样率,但它们也会导致 FFT 显示的频率分辨率降低。
如果信号本身不受带宽限制,则可以将低通滤波器应用于信号以限制其频率内容(图 5)。这在经常测量相同类型信号并且可以将专用低通滤波器与示波器一起使用的情况下尤其适用。
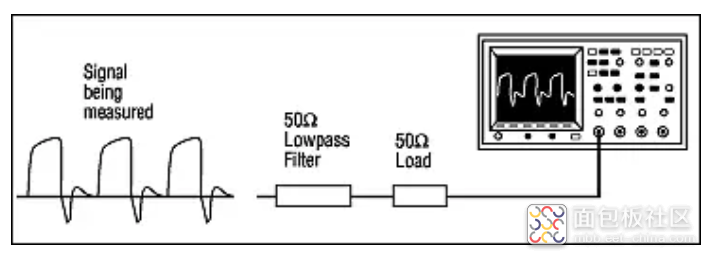
图 5:低通滤波器可用于限制信号的带宽,避免混叠。
泄漏*
FFT 针对有限长度的时间记录进行操作,试图估计傅立叶变换,该变换会对所有时间进行积分。FFT 针对有限长度的时间记录进行操作,但其效果是在所有时间上复制有限长度的时间记录(图 6)。对于图 6a 所示的波形,有限长度的时间记录很好地表示了实际波形,因此 FFT 结果将非常接近傅立叶积分。
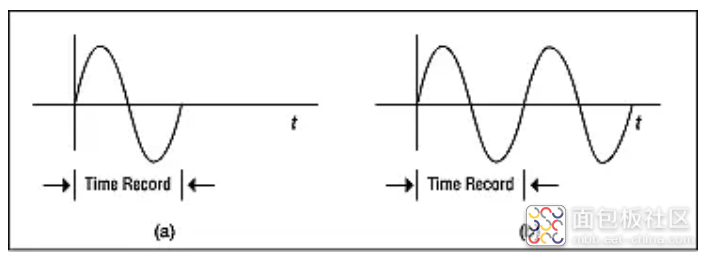
图 6
(a) 完全适合一个时间记录的波形。
(b) 复制时不会引入任何瞬变。
但是,波形的形状和相位可能会使得在复制波形的所有时间时引入瞬变,如图 7 所示。在这种情况下,FFT 频谱不是傅立叶变换的良好近似值。
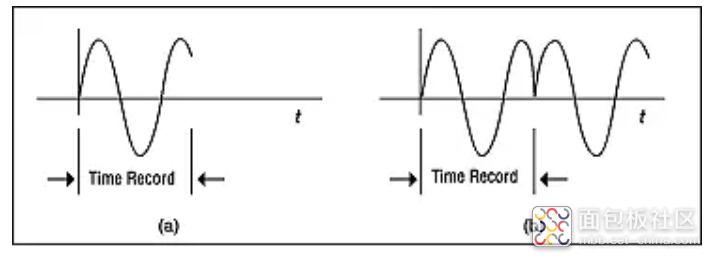
图 7
(a) 不完全适合一个时间记录的波形。
(b) 复制时,会引入严重的瞬变,导致频谱泄露。
由于示波器用户通常无法控制波形如何适应时间记录,因此通常必须假设可能存在不连续性。这种称为泄漏的效应在频域中非常明显。瞬变会导致谱线(应该看起来很细)扩散,如图 8 所示。 * 有关相关实验,请参阅“在示波器上教授数学,第 3 部分”。
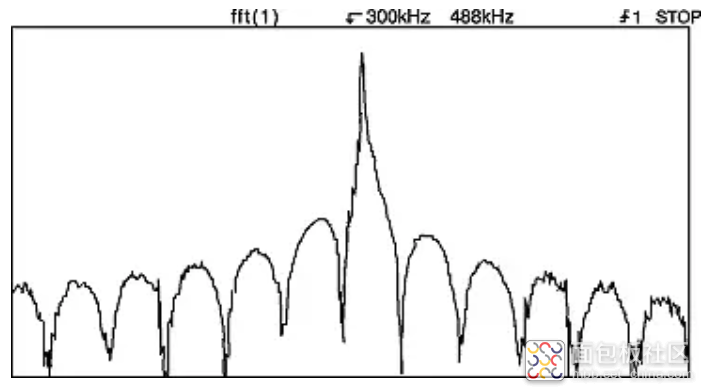
图 8 当通常很细的谱线在频域中扩散时,就会发生泄漏。
解决泄漏问题的方法是将时间记录末端的波形强制为零,这样在复制时间记录时就不会出现瞬变。这是通过将时间记录乘以 WINDOW 函数来实现的。当然,窗口会修改时间记录,并在频域中产生自己的效果。对于设计合理的窗口,频域效果比不使用窗口要好得多。1 Keysight 示波器中有四种窗口函数:Hanning、Flattop、矩形和指数。
当接近时间记录的任一端时,Hanning 窗口可平滑过渡到零。图 9a 显示时间域中的正弦波,而图 9b 显示将应用于时间域数据的 Hanning 窗口。图 9c 显示了窗口化的时间域记录。即使时间域信号的整体形状发生了变化,频率内容也基本保持不变。与正弦波相关的谱线在频域中稍微扩展,如图 10.2 所示(图 10 在频率轴上展开,以清楚地显示频域中窗口的形状。)
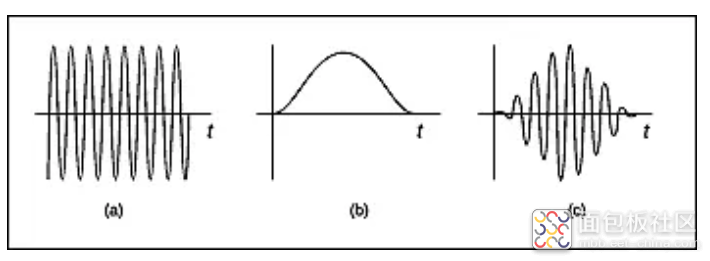
图 9
(a) 原始时间记录。
(b) 汉宁窗。
(c) 加窗时间记录。
窗口的形状是幅度精度和频率分辨率之间的折衷。与其他常见窗口相比,汉宁窗以稍低的幅度精度为代价提供了良好的频率分辨率。
FLATTOP 窗口在频域中具有更宽(和更平坦)的特性,如图 11 所示。(同样,该图在频率轴上展开,以清楚地显示窗口的效果。)频域中谱线的顶部更平坦,可提高幅度精度,但代价是频率分辨率较差(与汉宁窗相比)。
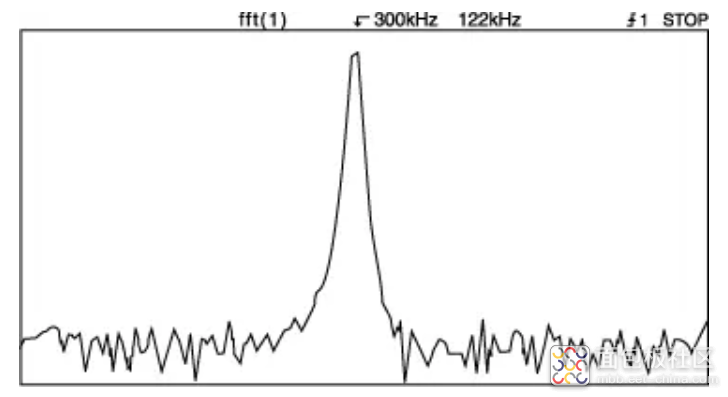
图 10 汉宁窗在频域中具有相对较窄的形状。
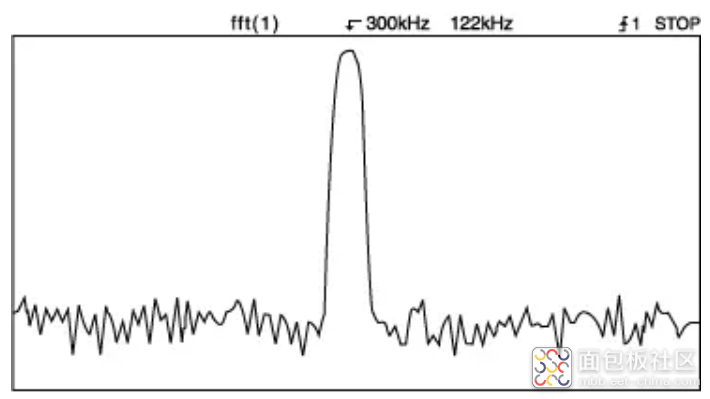
图 11:平顶窗口在频域中具有更宽的平顶形状。
矩形窗口(也称为均匀窗口)实际上根本没有窗口;所有样本保持不变。虽然均匀窗口可能会出现严重的泄漏问题,但在某些情况下,时间记录中的波形在记录的两端具有相同的值,从而消除了 FFT 引入的瞬态。这种波形称为自窗口。正弦脉冲、脉冲和衰减正弦波等波形都可以自窗口化。
图 12a 显示了典型的瞬态响应。如图所示,波形是自窗口化的,因为它在时间记录的长度内消失,从而减少了泄漏问题。
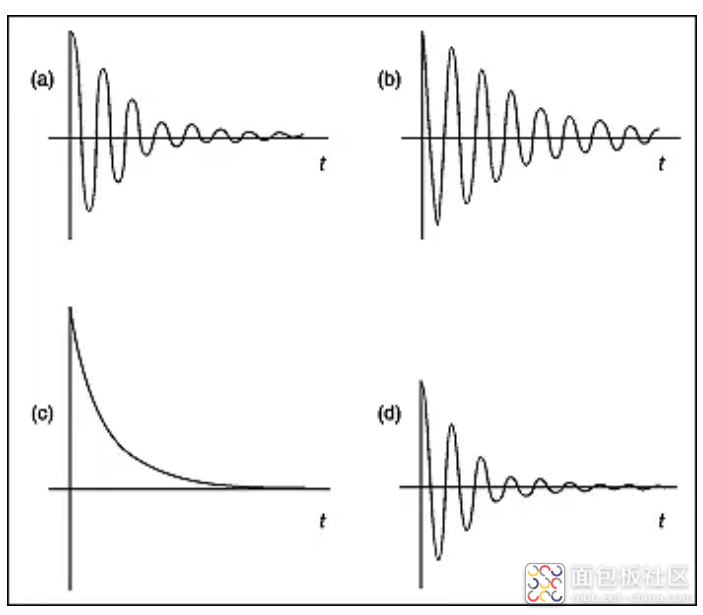
图 12
(a) 自窗口化的瞬态响应。
(b) 需要窗口化的瞬态响应。
(c) 指数窗口。
(d) 窗口化的瞬态响应。
如果波形在时间记录内没有消散(如图 12b 所示),则应使用某种形式的窗口。如果将诸如 Hanning 窗口之类的窗口应用于此波形,则时间记录的开始部分将被强制为零。这恰恰是瞬态的大部分能量所在的地方,因此这种窗口是不合适的。
在这种情况下,具有衰减指数响应的窗口很有用。波形的开始部分不会受到干扰,但时间记录的末尾被强制为零。时间记录的开头可能仍存在瞬态,但此瞬态不是由 FFT 引入的。事实上,它就是被测量的瞬态。图 12c 显示了指数窗口,图 12d 显示了将指数窗口应用于图 12b 时产生的时域函数。指数窗口不适合测量除瞬态波形以外的任何波形。
1时域窗口在频域中的作用类似于扫频频谱分析仪中分辨率带宽滤波器的形状。
2应用窗口函数后,频域中的完美正弦波的形状是窗口函数的傅里叶变换。
选择窗口
大多数测量都需要使用窗口,例如 Hanning 或 Flattop 窗口。这些是典型频谱分析测量的合适窗口。在这两个窗口之间进行选择涉及频率分辨率和幅度精度之间的权衡。使用时间域解释了泄漏发生的原因后,现在用户应该切换到频域思维。窗口频域滤波器的通带越窄,分析仪就能更好地区分两个紧密间隔的谱线。同时,谱线的幅度将变得不确定。相反,窗口的频域滤波器越宽越平坦,幅度测量就越准确,当然,频率分辨率也会降低。在两个这样的窗口函数之间进行选择实际上只是在频域中选择滤波器形状。
矩形和指数窗口应被视为特殊情况的窗口。在可以保证没有泄漏效应的情况下使用矩形窗口。指数窗口用于输入信号为瞬态的情况。有关窗口的更多信息,请参阅参考文献 2 和 6。
References:
- Brigham, E. Oran, The Fast Fourier Transform and Its Applications., Englewood Cliffs, NJ: Prentice-Hall, Inc., 1988.
- Hewlett-Packard
Company. "Fundamentals of Signal Analysis", Application Note 243,
Publication Number 5952-8898, Palo Alto, CA, 1981.
- McGille Clare D. and George R. Cooper. Continuous and Discrete Signal and System Analysis.
New York: Holt, Rhinehart and Winston, Inc.,1974. - Ramirez, Robert W. The FFT Fundamentals and Concepts. Englewood Cliffs, NJ: Prentice-Hall, Inc., 1985.
- Stanley,
William D., Gary R. Dougherty and Ray Dougherty. Digital Signal
Processing, 2nd ed. Reston, VA: Reston Publishing Company, Inc., 1984.
- Witte, Robert A. Spectrum and Network Measurements. Englewood Cliffs, NJ:
Prentice-Hall, Inc., 1991.






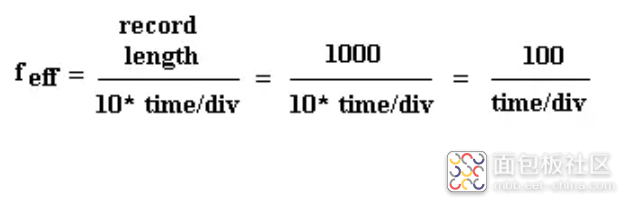












 /4
/4 
文章评论(0条评论)
登录后参与讨论