原创 天才的算法

天才和普通人的区别就是：

 几千年前，几百年前天才提出的方法（思想），发现的规律， 到现在普通人都很难解！

1、欧几里得（公元前325年-公元前265年），“辗转相除法”求解最大公约数

设两数为a、b(a>b），求a和b最大公约数(a，b）的步骤如下：用b除a，得a÷b=q......r1(0≤r1）。若r1=0，则 （a，b)=b；若r1≠0，则再用r1除b，得b÷r1=q......r2 (0≤r2）.若r2=0，则（a，b)=r1，若r2≠0，则继续用r2除r1，……如此下去，直到能整除为止。其最后一个非零除数即为（a，b）。

“辗转相除法”对数学界影响深远，基于此开创了很多领域。

2、牛顿 （1643-1727） ，大名鼎鼎的 Isaac Newton

“牛顿迭代法”

设r是

的根，选取

作为r的初始近似值，过点

做曲线

的切线L，L的方程为

，求出L与x轴交点的横坐标

，称x₁为r的一次近似值。过点

做曲线

的切线，并求该切线与x轴交点的横坐标

，称

为r的二次近似值。重复以上过程，得r的近似值序列，其中，

称为r的

次近似值，上式称为牛顿迭代公式。

用牛顿迭代法解非线性方程，是把非线性方程

线性化的一种近似方法。把

在点

的某邻域内展开成泰勒级数

，取其线性部分（即泰勒展开的前两项），并令其等于0，即

，以此作为非线性方程

的近似方程，若

，则其解为

， 这样，得到牛顿迭代法的一个迭代关系式：

。

已经证明，如果是连续的，并且待求的零点是孤立的，那么在零点周围存在一个区域，只要初始值位于这个邻近区域内，那么牛顿法必定收敛。 并且，如果不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。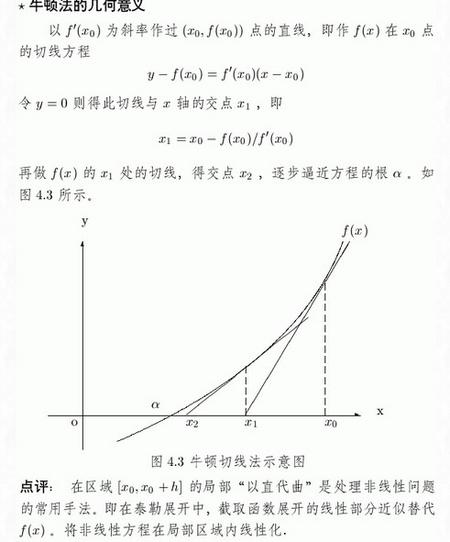



牛顿迭代法可以应用在 FPGA/ASIC 除法运算中，详见《数字信号处理的FPGA实现》