原创 图解数字电路中标准式的对偶式和反函数求解

        数字电路中经常遇到求标准式（最大项或最小项表达式）的对偶式和反函数求解问题。以前刚学数字电路时，总是对原函数，原函数的反函数及其对偶式之间的关系，通过标准式求解时也常感觉有些头晕，最近发现把三者之间的关系总结如下图之后就很容易理解并且求解标准式的对偶式和反函数求解问题也变得很简单了。

                                                      图（一）

从图（一）中可以看出：

1.任何一个函数两种标准式中所含的最小项m_i、最大项M_j的编号i和j是互不重复而且相互补充的。

2.n变量共有2ⁿ个不重复的编号，最大项和最大项的编号为从0至（2ⁿ-1）。

如图（一）中左边的方框中的关系。

3.由若干个最小项之和表示的函数F，其反函数可用等同个对应的最大项之积来表示。

4.相同编号的最小项和最大项之间关系为互补关系。

因此当要求解下面的题目时只要记住图（一）------比单独地记上面四点关系好得多且不容易弄混淆，然后分别对应找出关系式就可以很快解出：

题（1）：若已知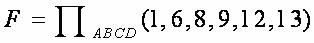要求它的对偶式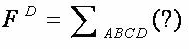

在图（一）中找到如下图中的蓝色线所示的关系：

则不难准确地得到:2ⁿ-1=15,15-1=14,15-6=9,15-8=7,15-9=6,15-12=3,15-13=2.

即其对偶式为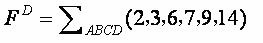：，其他类似的题目也可以类似导出。

又如题（2）：问逻辑函数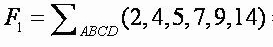和之间满足（ ）关系？

A,对偶         B，相等            C,香农展开             D，反演

只需将F1和F2（项数相同且每项标号一样）分别在图（一）中找出如下图蓝线间的关系：

可知二者之间为反演关系（互为反函数）。