标签: crc校验

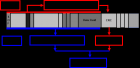
CRC 与 Checksum区别： 相信大家在CAN Msg或者ETH PDU中经常会看到Checksum这种信号。提到Checksum，就必须要说明一下CRC校验，很多工程师会概念混淆，认为两者是同一个东西，实则它们有很大的区别。 第一 、 两者 存放位置不同。 CRC校验： 循环冗余检查（ CRC ）是一种数据传输检错功能，对数据进行多项式计算，并将得到的结果附在帧的后面，接收设备也执行类似的算法，以保证数据传输的正确性和完整性。 通过 CRC 概念可以得知， CRC 存放在 CRC 场，而 Checksum 存放在数据场之中，一般在数据场的第一个字节或者最后一个字节。 图1 标准数据帧格式 第二 、 两者应用场景 不同。 在CAN报文帧中，CRC校验是发送器根据发送的bit进行多项式计算校验，结果放在15bit长度的CRC位。接收器也是用相同的多项式计算总线上的数据，与接收到的校验值进行比较，相同则表示帧正确接收，并在ACK时隙中发送显性状态，覆盖发送器的隐性位；如果不同接收节点在ACK界定符之后发送错误帧。 图2 CRC校验原理 CRC校验是为了保证数据从一个CAN收发器发送到另外一个收发器的信号完整性，而数据场中Checksum校验算法是为了校验数据被正确的打包与解包，并且Checksum算法是可以自行制定的，计算规则的灵活度高。 Checksum 的应用场景 对于Checksum而言，它的应用场景有以下三点： 1. 确保数据正确打包 有些ECU内部的变量在传递到CAN收发器之前就有可能发生错误，这种类型的错误CAN收发器是无法检测到的。报文中的信号和Checksum校验是在应用层完成的，将报文中的各个字节进行校验，报文和Checksum一起发送，并且在接收节点进行解析，从而确保数据链路完整和数据正确打包。 2 . 实现数据加密 CAN网络是开放性的，CAN节点可以随时加入到总线当中，为了保证通信的安全性，ECU传输的关键控制信号需要进行加密，报文的发送方和接收方使用相同的Checksum算法作为数据加密的密钥。接收方对比秘钥，如果不同，此条报文的数据不被使用，从而避免被其他节点的数据影响。Checksum算法不在DBC等数据库文件中说明，可以单独保密，从而确保了数据的加密。 3 . 提高 数据 的可信度 一帧报文在多个字节中可能出现位错误，一般情况下CRC8校验的错误率为1/256，crc16校验的错误率为1/65536，crc32校验的错误率为1/(65536*65536)。通过Checksum校验可以提高数据的可信度。 由于Checksum的作用，其也常应用在车载以太网当中。 在CAPL中 Checksum信号 实现 通常情况下，Checksum和LiveCounter信号是成对出现的。在CANoe中使用仿真节点与真实控制器交互，需要将LiveCounter和Checksum信号仿真，这样才能成功通信。LiveCounter长度为4bit，它是用于报文发送计数的生命信号，每发送一帧报文后就对该LiveCounter位加1，会在0~15之间循环增加。在报文其他信号没有改变时，LiveCounter实时更新使得Checksum信号跟着更新，提高校验的准确性。那么LiveCounter信号该如何仿真呢？ 下面以CAN总线DBC为例，介绍在CAPL中实现LiveCounter和Checksum校验仿真。 CAPL是CANoe和CANalyzer中可用的类C的编程语言。CAPL中程序块的执行由事件控制，在专用的编译器中开发和编译，这样可以访问数据库中的所有对象以及系统变量，被汽车电子工程师们广泛使用。 下图为LiveCounter计算的代码，为了保证数据的准确性，进行一次Checksum计算，这样就可以实现LiveCounter信号的仿真。 图3 LiveCounter计算代码 下图为示例报文中各个信号位置排布关系，在此报文中，Checksum校验方式为前七个字节异或运算，将运算结果存放到最后一个字节。排布图中共有8个信号，它们的格式为Motorola格式，也就是俗称的大端模式。 图4 报文中信号排布 CAPL只能访问到报文中的信号，无法访问到报文中的每个字节，要进行Checksum计算，需要根据信号排布把前七个字节的真实值重新组合存放在一个byte类型的数组当中，然后对这个数组异或运算获取的结果为该报文中Checksum信号值。 对于不同长度的信号，需要声明不同类型的数组来存放不同的信号。byte类型长度为1字节，声明两个byte * 类型的数组（*为省略的数组名称）分别存放长度小于一字节的信号和重组后每个字节的真实值；int类型长度为2字节，声明int * 类型的数组存放长度为1-2字节的信号；long类型长度为4字节，声明long * 类型的数组存放长度为2-4字节的信号。下图为Checksum中信号长度小于1字节的字节重组示例代码。 图5 Checksum字节重组示例代码 另外，参与Checksum计算的是信号的真实值而不是物理值，如果信号中有偏移量和比例因子，在赋值时需要将信号加上偏移量，并除以比例因子以获得真实值。 图6 信号描述 为了保证和真实控制器通信正常，Checksum数据必须准确，Checksum计算步骤一般写成无返回值函数（void），在LiveCounter信号改变或者其他信号改变时调用计算。 正确计算的LiveCounter和Checksum信号曲线如下图所示。 图7 LiveCounter和Checksum信号曲线 总结 本文重点描述了CRC和Checksum信号的区别以及Checksum信号在CAPL中实现的方法。CAPL编程作为CANoe的灵魂，使CANoe满足仿真、分析、测试和诊断的各种复杂的要求，同时使CANoe的功能得以不断扩展。 北汇信息 作为Vector中国的合作伙伴，致力于为中国汽车客户提供优质的工具支持、解决方案以及测试服务。 注：图片来自于Vector。

CRC 校验：从原理到实现（二）   1、 收发端CRC校验的可选机制   CRC 校验是为了保证信息在发送端和接收端之间传输的完整性，所以除了在收发两端都要实现 CRC 计算之外，还需要确定一些具体的机制，主要的几种机制分类列举如下：   表 1-1 收发端 CRC 校验的六种机制   机制 发送端 接收端 初始寄存器值 校验序列 初始寄存器值 校验范围 正确判定 1 0 不操作 0 明文 结果 = 校验序列？ 2 0 不操作 0 明文 + 序列 结果 =0 ？ 3 0 逐位取反 0 明文 + 序列 结果 =Magic Num ？ 4 全 1 不操作 全 1 明文 结果 = 校验序列？ 5 全 1 不操作 全 1 明文 + 序列 结果 =0 ？ 6 全 1 逐位取反 全 1 明文 + 序列 结果 =Magic Num ？   初始寄存器。初始寄存器的值为 0 ，符合一般的 CRC 校验原理，也便于在 MATLAB 中计算。但是容易出现“前导 0 ”问题，即在明文序列之前插入或者删除 0 序列，这是由于 0 与 0 异为 0 。因此，将初始寄存器值设为全 1 可以避免“前导 0 ”的出现。发送端和接收端的初始寄存器值须保持一致以保证两端校验正确。   接收端的校验范围。可以选择明文或者明文 + 序列，若传输完整无误，明文的 CRC 计算结果等于收到的校验序列，明文 + 序列的计算结果归 0 。两者相比，后者实现流程简单。   Magic Num 。明文 + 序列的计算结果归 0 并不定能严格证明信息传输完整无误，无法检测“拖尾 0 ”问题，即在序列之后插入或者删除 0 序列，同样是由于 0 与 0 异为 0 。所以引入了 Magic Num 的机制，在发送端需要对校验序列逐位取反添加在明文序列之后发送，在接收端对明文 + 序列做校验，若结果等于 Magic Num 则说明信息传输完整无误。 Magic Num 是与生成多项式对应的序列，计算过程如下：   一般情况下，在接收端对明文 + 序列做计算，结果为 0 说明传输完整无误： ，其中 M 是明文序列， R 是校验序列， G 是生成多项式。   用 /R 表示 R 对 1 取反，我们得到： 因此，由接收端计算出的无差错的传输的校验和应该是： ，这就是 Magic Number 。   Magic Num的校验方法在网络传输的设计中比较常见，在 802.3 的 IP 核和 802.11 标准的附录框图中对 CRC32 校验的设计都采用了初始寄存器全 1 和 Magic Num 的方式 。   参考资料：   http://blog.sina.com.cn/s/blog_62d9edac01015lsd.html http://blog.csdn.net/highyyy/article/details/6208227   http://www.eefocus.com/Galois/blog/10-02/184555_16c21.html   http://wenku.baidu.com/view/a5b7d38002d276a200292e80  

【原始内容来自网络，加入了部分自己的理解。】 概念： CRC ： Cyclic Redundancy Check, 循环冗余校验。 利用除法和余数的原理来对数据进行校验和纠错。特征是信息字段和校验字段的长度可以任意选定。 多项式： 任意一个二进制数可以与一个系数非1即0的多项式相对应，如1011对应多项式为x^3+x+1。一个nbit的二进制数可对应一个(n-1)次幂的多项式。 模二除法： 与算术除法类似，但不向上一位借位，每一位除的结果不影响其他位，实际上就是异或。 生成多项式： 生成多项式也是一个二进制数，它是发送方和接收方的一个约定，在整个传输过程中，这个数始终保持不变。 在发送方，用生成多项式对信息多项式做模二除法，产生校验码。在接收方，用生成多项式对收到的编码多项式做模二除法检测，并确认错误位置。 生成多项式的最高位和最低为必须为1。 常见于标准的生成多项式如下。     原理： 若设码字长度为N，其中信息字段长度为K，校验字段长度为R，则有N=K+R。对于CRC码集中的任一码字，存在且仅存在一个生成多项式g(x)，使得 m(x)*(x^R)+r(x) = V(x) = A(x)g(x)+d(x); 其中，m(x)为(K-1)次原始的信息多项式； r(x)为(R-1)次校验多项式（即校验和，是用m(x)向左移位Rbit后的数对生成多项式做模二除法所得的余数）； g(x)为R次生成多项式； V(x)为发送方传递给接受方的CRC码字； d(x)为V(x)对g(x)做模二除法所得的(R-1)次余数，正确情况下应该为0。   在发送方，根据已知的N、K、R、m(x)、g(x)，计算出r(x)，生成V(x)，作为最终的码字发出； 在接收方，根据已知的N、K、R、V(x)、g(x)，计算得出A(x)、d(x)，若d(x)为0，说明校验结果正确。若d(x)不为0，则说明数据在传输过程中出现了错误。   其他特性： 由于CRC的计算基于除法，任何多项式都无法检测出一组全零数据出现的错误或前面丢失的0； 所有只有一个bit位的错误都可以被至少有两个非0系数的任意多项式检测到； CRC可以检测出所有间隔距离小于生成多项式阶次的两bit错误。 CRC是散列函数（hash算法）的一种，也存在一定的冲突概率。所以生成多项式的设计和选择至关重要。 生成多项式最重要的属性是长度。生成多项式必须是不可分解多项式，即除了1与它自身之外不能被任何其他的多项式整除。   生成多项式的选择还要取决于信息字段的长度。如果我们希望在接收方检测时能明确知道具体的错误位置，那么余数值的集合就要大于等于码字的长度，要满足：2^(R-1) = N，也即：2^(R-1) = (R+K)。 由此可知，CRC-4适合用来检测4bit以内的信息字段； CRC-8适合用来检测120bit以内的信息字段； …