标签: ADC测试系统

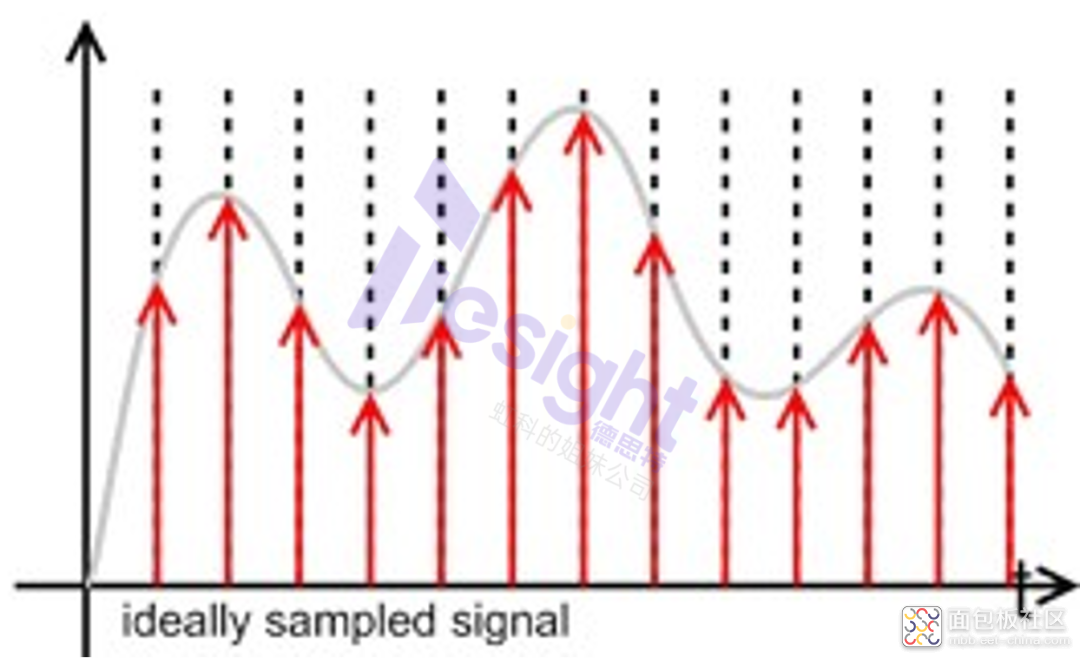
​前一章详解了ADC直方图测试的两种核心方法：线性斜坡法和正弦波法，涵盖DNL/INL计算、测试参数优化及德思特高精度测试方案。 【前文回顾】 技术干货 | 精准测试，高效分析——ADC直方图测试技术详解-CSDN博客 本章将继续介绍DAC频率响应特性，探讨sinc函数导致的信号衰减规律，对比数字滤波与模拟滤波两种补偿技术： 简介 TS-ATX7006 的 AWG（任意波形发生器）模块通过 D/A 转换器产生输出信号。要知道，DAC 的输出在整个频率范围内并不平坦。一般来说，输出信号的频率范围从直流到采样频率的一半（1/2fs）。D/A 转换器的频率响应取决于 sin(x)/x（或 sinc）函数。 理想的采样信号会在采样时刻之间对电压进行内插。这将导致平坦的频率响应。 典型的 D/A 转换器将保持输出恒定，直到下一个采样时刻（采样和保持输出）。这将导致阶跃输出，造成非平坦频率响应。每个信号的采样越少，频率响应的衰减就越大。 信号时域中的阶跃会转化为高频频谱图像。这些图像可以在采样率 +/- 信号频率处找到。见下图。靠近 y 轴的黑线为信号频率，采样频率附近的图像标为红色。图像也会随着 sinc 频率响应而衰减，并且取决于 AWG 的模拟（输出）带宽，这是不言而喻的。可以通过插值（数字滤波）和模拟滤波来减少图像的影响。 数字滤波会提高有效采样率，从而将图像频率移至更高频率。（低通）模拟滤波器会使输出平滑，从而抑制高频信号。 sinc 函数的方程见上图。0.1dB 频率平坦度约为奈奎斯特频率的 17%（奈奎斯特频率 = 1/2 采样频率）。有两种方法可以补偿 sinc 频率响应：数字滤波和模拟滤波。数字滤波或预均衡技术为 DAC 处理数字数据，可提供 0.1 dB 至 96% 奈奎斯特频率的平坦度。模拟滤波或后均衡技术处理 DAC 的模拟输出数据，可提供 0.1 dB 至 50%奈奎斯特频率的平坦度。这两种方法都会降低（恶化）低输出频率的信噪比。 Sinc计算器 使用 sinc 计算器可以计算在指定频率和采样频率下由于 sinc 响应而产生的衰减： Sinc计算器展示图，如有需要可联系德思特获取工具链接 德思特ADC测试平台TS-ATX7006特点 ✓ 完全集成的ADC测试解决方案 ✓ 采样频率高达200/400 MHz ✓ 无与伦比的信号发生质量和精度 ✓ 支持所有线性/动态测试 ✓ 灵活和通用的数字IO ✓ 扩展分析软件ATView\WaveAnalyzer ✓ 静态、直方图测试 ✓ 易于用户自定义的测试脚本 ​

​ 在现代电子系统设计与高速通信、信号处理、雷达探测、医疗成像以及各种工业自动化应用中，模数转换器（ADC）和数模转换器（DAC）扮演着至关重要的角色。ADC负责将模拟信号精确且高效地转换为数字信号，以便于进行数字信号处理和数据传输；而DAC则执行相反的功能，它将数字数据流还原为高质量的模拟信号，以供实际设备或系统使用。 随着技术的不断进步，尤其是对于5G通信、航空航天及国防等领域的严苛要求，高速、高精度、高分辨率以及大动态范围的ADC和DAC变得越来越重要。为了深入探究这些关键器件的基础性能指标，德思特将引领您走进ADC和DAC的静态参数测试世界。本篇文章将为您介绍ADC中的一个关键概念——转换点。 一、介绍 A/D转换器的线性参数计算（INLE、DNLE等）基于器件的转变点（或跳变点）。为了确定ADC的转变点，应将具有足够步长的模拟斜坡表征器件的吸纳后输入。根据测量的代码可以确定转变点。 德思特ADC测试系统TS-ATX7006和软件TS-ATView7006有两种确定跳变点的方法： ● 跳变点搜索方法：算法“搜索”跳变点。考虑测量代码在结果数组中的位置。 ● 代码排序方法：代码在结果数组中出现的次数是LSB步长的度量。 （一）跳变点搜索法 搜索从代码x到代码x+1(x - x+1)的跳变点，首先搜索数据数组中代码x的第一次出现以及数据数组中代码x+1的最后一次出现，这就是跳变点的搜索数组。 代码x和小于代码x的出现次数均计入该区域。跳变点位于首次找到代码x加上该计数器值（在该区域中找到代码x及更少代码的次数）的位置。 开始和结束时丢失的代码将通过理想的转换器步骤 (DNLE=0) 进行推断，并以第一个找到的跳变点作为参考。最后，跳变点是从最后找到的跳变点推断出来的。所有其他缺失代码都会导致 DNLE为-1：跳变点位于与其前一个跳变点相同的位置。 噪声或测量分辨率不足可能导致DNLE小于1 LSB。 举 例说明 1、无噪声 捕获的数字数据阵列： 跳变点0→1: 搜索区域：位置0-11。 计数：6 跳变点位于位置5至6。跳变点电压为： Vtrp=Vstart+count*Vstep-1/2Vstep 其中： Vstart=提供的斜坡的起始电压。 startposition=首次找到代码的位置，此处为位置0。 count=找到代码0的次数 Vstep=提供的斜坡的电压步长。 2、 带有噪声 捕获的数字数据阵列： 跳变点0→1: 搜索区域：位置0-11。 计数：5 跳变点位于位置4至5。 跳变点1→2: 搜索区域：位置3-14。 计数：8（6次代码1+2次代码0） 跳变点位于位置10至11。 3、丢失代码 捕获的数字数据阵列： 跳变点0→1和0→2: 搜索区域：位置0-11。 计数：5 两个跳变点均位于位置4至5。 （二）排序代码方法 所有代码都在数据数组中排序。排序后，数据数组从所有测量代码0开始，然后是代码1，依此类推。因此，测量数据中代码的位置不相关。使用排序代码方法不会发生小于-1的DNL错误。 示例 排序前捕获的数字数据数组： 排序后捕获的数字数据数组： ​

​在现代电子系统中，模数转换器（A/D转换器）作为模拟信号与数字信号之间的关键桥梁，其性能直接影响系统的精度、速度和可靠性。为了深入理解A/D转换器的性能表现，工程师需要掌握一系列关键特性参数，包括静态指标（如线性度、偏移误差、增益误差）和动态指标（如信噪比、谐波失真、动态范围）。 这些参数不仅决定了转换器的基本精度，还影响着系统在高频、高速或高精度应用中的表现。 本文系统性地整理了A/D转换器的核心特性术语，从孔径延迟、抖动等时序参数，到微分非线性（DNL）、积分非线性（INL）等线性度指标，再到信噪比（SNR）、总谐波失真（THD）等动态性能参数，逐一解析其定义、测试方法及对实际应用的影响。 1、孔径延迟 时钟有效边沿之后，到输入信号被采集或保持以进行转换的时间。 2、孔径抖动 要开始突发测量，请从菜单栏中选择“burst”。 3、（转换）延迟或流水线延迟 启动一次转换到第一个转换数据出现在输出端之间的时钟周期数。每个采样数据在流水线延迟加上采样后的输出延迟后可用。 4、转换时间 完成一次转换所需的时间。转换时间不包括采集时间、多路复用器的设置时间或其他元件时间，因此转换时间可能小于 “吞吐时间”。 5、端点线与最佳拟合线 ● 端点线： 连接第一个和最后一个转换点的直线，仅使用首尾两点计算参考线，端点误差图的首尾点始终为零。 ● 最佳拟合线： 使用所有转换点，通过最小二乘法线性回归拟合的直线，使误差分布对称，更能反映整体线性度。 6、直流共模误差 差分输入模数转换的指标，指两个输入端施加相同电压时输出码的变化。 7、微分增益误差 当施加给定幅度的高频正弦波时，不同直流输入电平下输出电平的差异（以 % 表示）。 8、微分非线性误差（DNL/DNLE） 实际模拟输入信号对应码增量的1LSB台阶与理想1LSB台阶的最大偏差。 ● 意义： 静态指标，与动态指标信噪比（SNR）相关。DNL偏离零越大，SNR可能越差，但无法直接通过DNL预测噪声性能。 9、微分相位误差 两个不同直流输入电平下，重构的小信号正弦波输出相位的差异。 10、满量程误差 最后一个转换点与理想转换点的误差，等于增益误差与偏移误差之和。 11、增益误差 满量程误差减去偏移误差，反映参考线（端点或最佳拟合线）斜率与理想传输特性斜率的偏差。 计算公式：(N−1)/a−(N−1)，其中N为转换点数，a为参考线斜率。 12、积分非线性误差（INL/INLE） 传输特性与参考线（端点线或最佳拟合线）的偏离，不包含量化误差、偏移误差和增益误差，是衡量传输函数直线度的指标，可能大于微分非线性误差。 ● 意义： 静态指标，与动态指标总谐波失真（THD）相关。INL偏离零越大，THD可能越差，但无法直接通过INL预测失真性能。 13、丢失码 理想情况下应出现的输出码在实际转换中未出现的现象。 14、非单调性 输入电压单调增加时，输出码非单调变化的现象（如码值先增后减）。 15、偏移误差 第一个转换点与理想转换点的误差（端点计算）。对于最佳拟合线，偏移误差为最佳拟合参考线与理想传输线的偏移量。 16、量化误差 模数转换器输出在1LSB范围内保持不变，导致输入电压在台阶内变化时产生的误差。 ●范围：理想情况下为0到1LSB；若采用半LSB偏移，误差范围为−1/2LSB 到+1/2LSB。 17、信噪失真比（SINAD） 信号（或载波）功率与采样频率一半以下所有其他频谱分量（不含直流）功率的比值。 18、信噪比（SNR） 输出信号幅度与输出噪声电平（不含谐波和直流）的比值。 ● 影响因素： a.量化噪声：分辨率越高，LSB越小，量化噪声越低； b.转换器自身噪声； c.应用电路噪声； d.抖动：高频下抖动影响增大，导致 SNR 下降。 ● 理论公式： 全量程正弦波输入时，SNR=20×log(2n−1×6)≈6.02n+1.76dB（n为分辨率）。 19、无杂散动态范围（SFDR） 信号功率与频谱中最高杂散信号功率的分贝差。 20、总谐波失真（THD） 信号（或载波）功率与谐波频谱分量（载波倍数频率）功率的比值，TS-ATX7006默认计算7次谐波（可调整）。 21、总未调整误差（TUE） 包含线性度误差、增益误差和偏移误差的综合指标，反映与理想器件性能的最坏情况偏差。 ​