标签: 信号调节

5 模数转换 器 5.1 基本概念 模数转换器（缩写为 A/D ，或 ADC ， A2D ， A-to-D ）的类型从分立电路到单片 IC （集成电路），以及高性能混合电路、模块，甚至是盒子等等不一而足。此外，这种转换器还有定制的标准单元和半定制的专用集成电路（ ASIC ）产品。 A/D 转换器把通常为电压的模拟数据转换成等效的、与数字数据处理器件兼容的数字格式。 A/D 转换器的关键特性包括绝对和相对精度、线性度、无失码、分辨率、转换速度、稳定性，以及价格。很多情况下，在把价格作为主要考虑因素时，单片 IC 版本（集成电路）是最具效率的。最常见的 A/D 转换器基于逐次逼近技术，因为在速度和精度之间要获得内在的良好折中。不过其它常用技术也用于各种各样的用途，特别是在没有高转换速率要求时。这些技术包括双斜率、四斜率、脉宽调制（ PWM ）、电压至频率（ V/F ）转换器，以及电阻至频率（ R/F ）转换器。 A/D 转换的技巧已得到充分开发。这里我们简要评述一些常用的这类转换器架构，至于详细的阐述读者可参阅相关专业文献。 最有名的数字码是二进制（ 2 基数）。二进制码最常见的是表示整数，即具有 n 位的自然二进制整数码，最低有效位（ LSB ）具有 的加权（即 1 ），下一位具有 的加权（即 2 ），依此类推直到 MSB （最高有效位），其加权为 （即 ）。二进制数的值是把所有非零位的加权相加得到。合计加权位后，即得到具有从 0 到 的任何值的唯一数字。每个附加的尾随零位，如果有的话，实质上就是原值大小的加倍。 转换来自模拟传感器的信号时，因为满量程与分辨率的位数无关，一种更实用的编码是分数二进制，其总是可以归一化为满量程。如果所有整数值都被 除，那么整数二进制就可以用分数二进制来表示。例如， MSB 具有 1/2 （即 ）的加权，下一位具有 1/4 （即 ）的加权，如此等等直到 LSB ，该位具有 （即 ）的加权。加权位相加后，形成一个任意 值构成的数字，从 0 到满量程的（ 1- ）。附加的位只是提供更为精细的度量，不会影响满量程范围。为了表示这些关系，表 1 列出 5 位的带有二进制加权的 1 和 0 的值的 16 种排列，以及表示为十进制和二进制整数与分数的等效数字。 在自然二进制中所有位是“ 1 ”时，分数值则是 1- ，或归一化为满量程小于 1 LSB （例如 1-1/16=15/16 ）。严格来说，写成“整数点”时，上面表示的数字是 0.1111 （ =1-0.0001 ）。不过，几乎普遍采用的是，把代码简单写为整数 1111 （即“ 15 ”）与相应数字的分数形式即得：“ 1111 ” 1111/(1111+1) ，或 15/16 。 表 1. 整数和分数二进制编码 十进制分数 二进制分数 MSB 1/2 Bit2 1/4 Bit3 1/8 Bit4 1/16 二进制整数 十进制整数 0 0.0000 0 0 0 0 0000 0 1/16 （ LSB ） 0.0001 0 0 0 1 0001 1 2/16=1/8 0.0010 0 0 1 0 0010 2 3/16=1/8+1/16 0.0011 0 0 1 1 0011 3 4/16=1/4 0.0100 0 1 0 0 0100 4 5/16=1/4+1/16 0.0101 0 1 0 1 0101 5 6/16=1/4+1/8 0.0110 0 1 1 0 0110 6 7/16=1/4+1/8+1/16 0.0111 0 1 1 1 0111 7 8/16=1/2 （ MSB ） 0.1000 1 0 0 0 1000 8 9/16=1/2+1/16 0.1001 1 0 0 1 1001 9 10/16=1/2+1/8 0.1010 1 0 1 0 1010 10 11/16=1/2+1/8+1/16 0.1011 1 0 1 1 1011 11 12/16=1/2+1/4 0.1100 1 1 0 0 1100 12 13/16=1/2+1/4+1/16 0.1101 1 1 0 1 1101 13 14/16=1/2+1/4+1/8 0.1110 1 1 1 0 1110 14 15/16=1/2+1/4+1/8+1/16 0.1111 1 1 1 1 1111 15 为方便起见，表 2 列出高至 20 位数字的二进制位加权。不过绝大多数传感器的实际范围很少超过 16 位。 分配给 LSB 的加权是具有 n 位数字的分辨率。 dB 列表示 LSB 值与 1 （满量程）的比值取对数（以 10 为底），再乘以 20 。每个后续的 2 的幂次方表示 6.02dB 的变化（即 ）或“ 6dB/ 倍频程”。 表 2. 二进制位加权和分辨率 BIT 2-n 1/2n 分数 dB 1/2n 十进制小数 % ppm FS 20 1 0 1.0 100 1000000 MSB 2-1 1/2 -6 0.5 50 500000 2 2-2 1/4 -12 0.25 25 250000 3 2-3 1/8 -18.1 0.125 12.5 125000 4 2-4 1/16 -24.1 0.0625 6.2 62500 5 2-5 1/32 -30.1 0.03125 3.1 31250 6 2-6 1/64 -36.1 0.015625 1.6 15625 7 2-7 1/128 -42.1 0.007812 0.8 7812 8 2-8 1/256 -48.2 0.003906 0.4 3906 9 2-9 1/512 -54.2 0.001953 0.2 1953 10 2-10 1/1024 -60.2 0.0009766 0.1 977 11 2-11 1/2048 -66.2 0.00048828 0.05 488 12 2-12 1/4096 -72.2 0.00024414 0.024 244 13 2-13 1/8192 -78.3 0.00012207 0.012 122 14 2-14 1/16384 -84.3 0.000061035 0.006 61 15 2-15 1/32768 -90.3 0.0000305176 0.003 31 16 2-16 1/65536 -96.3 0.0000152588 0.0015 15 17 2-17 1/131072 -102.3 0.00000762939 0.0008 7.6 18 2-18 1/262144 -108.4 0.000003814697 0.0004 3.8 19 2-19 1/524288 -114.4 0.000001907349 0.0002 1.9 20 2-20 1/1048576 -120.4 0.0000009536743 0.0001 0.95 5.2 V/F 变换器 电压至频率（ V/F ）变换器能提供高分辨率的变换，因而适用于传感器的独特性能，诸如长期的整合应用（由数秒至数年），数字至频率变换（与 D/A 转换器结合），频率调制，电压隔离，以及任何需要的分频和倍频。这种变换器接收传感器的模拟输出，该输出可能是电压或电流（当然对后者的情况应该叫做电流至频率变换器）。在某些情况下，传感器可成为 A/D 转换器的一部分，如下节将阐明的。不过这里我们将只讨论电压至频率的变换，或者换言之，变换成每单位时间矩形脉冲的数量。因为脉冲能够选通（在给定时间间隔内选择）和计数，得出二进制数，所以这里的频率是数字格式的。所有 V/F 变换器都是积分类型的，因为每秒脉冲数或频率，正比于输入电压的平均值。 通过使用 V/F 变换器， A/D 可以在最简单和经济的方式下实现。把模拟电压转换为数字数码所需的时间，与 V/F 变换器的满量程频率和所需的分辨率相关。与逐次逼近器件相比，通常 V/F 变换器相对较慢，不过对绝大多数传感器应用，这种电路相当合适。用于 A/D 转换器时， V/F 变换器连接至计数器，后者在所需采样率下计时。举例来说，如果变换器的满量程频率是 32kHz ，计数器每秒采样 8 次，脉冲的最高数值能够通过对每一个采样周期的累计得出为 4000 ，这近似相应于 12 位的分辨率（见表 2 ）。通过采用同样的 V/F 变换器和计数器部件的组合，可以构建用于那些激励需要在一定时间内进行积分的应用的积分器。计数器在选通间隔累计脉冲，而不是累计每个采样周期脉冲的平均数。 V/F 变换器的另一个有用特性，是其脉冲能够容易地通过通讯线路传输。与高分辨率的模拟信号相比，脉冲信号极少受到环境噪声的影响。理想情况下，变换器的输出频率 f out 正比于输入电压 V in ： ， （ 22 ） 其中 f FS 和 V FS 分别是满量程的频率和输入电压。对给定的线性变换器，比值 f FS/ V FS=G 是常数，称为变换因子，从而 。 （ 23 ） 有几种熟知的 V/F 变换器类型。其中最常见的是多谐振荡器和电荷平衡电路。 图 24. 电压至频率变换器的多谐振荡器类型 多谐振荡器 V/F 变换器采用不同步的方波振荡器，其定时电容的充放电电流由输入信号控制（图 24 ）。输入电压 V in 由差分放大器（比如测量放大器）放大，其输出信号控制两个电压至电流转换器（晶体管 U 1 和 U 2 ）。一个精密多谐振荡器交替连接定时电容 C 至两个电流转换器。该电容以电流 i a 经由晶体管 U 1 充电半个周期。在下半个时间周期，电容以电流 i b 经由晶体管 U 2 放电。因为输入信号控制电流 i a 和 i b ，电容充电和放电的斜率也相应发生变化，由此改变了振荡频率。这种电路的明显优点是简单和可在很低功耗下工作，不过其抑制来自输入信号的高频噪声的能力不如电荷平衡架构那么好。 图 25. 电荷平衡 V/F 变换器 变换器的电荷平衡类型采用模拟积分器和电压比较器，如图 25 所示。这个电路具有的优点包括高速、高线性度和良好的噪声抑制。该电路的集成形式可由几家制造商获得，例如 AD 公司的 ADVFC32 和 AD650 ，美国国家半导体公司的 LM331 。这种变换器的工作方式如下。输入电压 V in 通过输入电阻 R in 加至积分器。积分电容以负反馈回路连接至运算放大器，运算放大器的输出电压与 -0.6V 的小的负阈值电压相比较。积分器产生锯齿形电压（图 27 ），该电压在到达阈值时在比较器输出产生瞬态信号。这个瞬态信号激活单稳态发生器，产生具有固定周期 t OS 的矩形脉冲。一个精密电流源产生恒定电流 i ，交替流过积分器的汇流结点或其输出。开关 S 1 由单稳态脉冲控制。当电流源连接至汇流结点时，其会传递一个精密确定的电荷包 Q=i t OS 至积分电容。同一个汇流结点也会通过电阻 R in 接收输入电荷，由此净电荷会在积分电容 C in 上累积。 图 26. 电荷平衡变换器的积分（ a ）和去积分（重置）（ b ）阶段 图 27. 电荷平衡变换器中的积分器输出 当到达阈值时，单稳态电路被触发，开关 S 1 改变其状态至高，由此开始重置阶段（图 26b ）。在重置阶段，电流源发送电流至积分器的汇流结点。输入电流使积分电容正向充电。在阈值和去积分结束之间的总电压由单稳态脉冲的周期确定： 。 （ 24 ） 单稳态电路的输出信号变低时，开关 S 1 把电流 i 切换至积分器的输出端，此时积分器不影响积分电容 C in 的状态。即电流源吸收一部分来自运算放大器的输出电流。这个时段称为积分周期（图 26a 和图 27 ）。积分期间，正的输入电压发送电流 I in= V in/ R in 至电容 C in 。这导致积分器由其正电压以正比于 V in 的速率下降。达到比较器阈值所需的时间为： 。 （ 25 ） 可见电容值不影响积分周期的时间长短。输出频率由下式确定： 。 （ 26 ） 所以，单稳态脉冲的频率正比于输入电压。该值也取决于积分电阻的质量，电流发生器的稳定性，以及单稳态电路自身。通过精心设计，这种类型的 V/F 变换器可达到非线性误差低于 100ppm ，能够产生由 1Hz 到 1MHz 的频率。 诸如电荷平衡 V/F 变换器这样的积分型变换器的主要优点，在于能够抑制大量的附加噪声。通过对被测量进行积分，减少了甚至完全消除了噪声。来自变换器的脉冲经计数器以选通周期 T 累计。于是计数器变成了具有如下式的传递函数形式的滤波器 ， （ 27 ） 其中 f 是脉冲频率。低频时，这个传递函数 H(f) 的值接近于 1 ，意味着变换器和计数器给出了正确的测量值。不过在频率为 1/T 时传递函数 H(1/T) 为零，意味着这样的频率被完全抑制。举例来说，如果选通时间 T=16.67ms ，对应于 60Hz 的频率，即动力电源线的频率，这是很多传感器中主要噪声的来源，那么 60Hz 噪声就会被抑制。此外，其倍频（ 120 、 180 、 240Hz 等等）也会被抑制。 5.3 双 斜率转换器 双斜率转换器已很普及；在手持式数字电压表和其它不需要快速转换的便携式仪器中几乎都在用。这种类型的转换器执行的是输入电压的间接转换。首先，该转换器把 V in 转换成时间的函数，然后由脉冲计数器把时间函数转换成数字码。双斜率转换器具有与电荷平衡变换器相同的优点；两者都抑制相应于积分定时的频率 1/T 。 双斜率转换器通常采用模拟组件（ OPAM ，开关，电阻和电容）和微控制器的组合，后者处理定时、控制逻辑和计数功能。 5.4 逐次逼近法转换器 得益于其高速（达 1MHz 的数据吞吐率）和高分辨率（ 16 位及更高），这种转换器以集成形式被广泛使用。其转换时间固定且与输入信号无关。因为在每次转换后内部逻辑和寄存电路都清零了，所以每次转换都是独一无二的，因而使这些 A/D 转换器适合于多路复用。转换器（图 28 ）包括精密电压比较器，移位寄存器和控制逻辑模块，以及把数字输出转换为模拟比较器的反馈输入的数字至模拟转换器（ D/A ）。 图 28. 逐次逼近 A/D 转换器框图 图 29. 逐次逼近 A/D 中的 3 位加权 转换方法包括把未知的输入 V in 与一个精确电压 V a 或由 D/A 转换器产生的电流比较。这种转换技术类似于用天平进行称重的过程，采用的则是一组 n 个二进制加权（比如 1/2kg 、 1/4kg 、 1/8kg 、 1/16kg 等等，直到总数 1kg ）。转换循环之前，所有寄存器必须清零，比较器输出为高。在 D/A 转换器输入端施加 MSB （ 1/2 量程），产生一个适当的模拟电压 V a ，其值等于满量程输入信号的 1/2 。如果输入电压仍然大于 D/A 电压（图 29 ），比较器维持为高，导致寄存器的输出为“ 1 ”。然后尝试下一位（ FS 的 2/8=1/4 ）。如果第二位没有增加足够的砝码来超过输入，比较器仍然为高（输出端为“ 1 ”），继续尝试第三位。不过如果第二位让天平翻转了，比较器变为低，导致寄存器中为“ 0 ”，然后尝试第三位。比较过程按下降位加权依次进行，直到尝试过最后一位。完成后，状态行指示转换结束，由寄存器读出对应于输入信号的有效数值的数据。 要使转换有效，输入信号 V in 必须不发生改变，直到所有位都尝试完毕，否则数字读数有可能是错误的。为了避免输入改变带来的任何问题，逐次逼近转换器通常附加采样保持（ S&H ）电路。这种电路具有短时模拟记忆功能，其对输入信号采样，并在整个转换循环期间以直流电压的形式存储。 5.5 分辨率扩展 典型的数据采集系统中，单片微控制器常常包含模数转换器，其最大分辨率一般限于 10 位。若内置转换器的分辨率较高，达 12 甚至 14 位，成本就会变得过于高了。在大多数应用中，要正确表示激励（输入分辨率 R 0 ）的最小增量， 10 位可能远远不够。有几种方法解决这个问题。其中之一是在 A/D 转换器之前使用放大器。例如增益为 4 的放大器会有效增加输入分辨率达两位，比如从 10 增加到 12 。当然付出的代价是放大器特性的不确定性。获得高分辨率的另一种方法，是采用双斜率 A/D 转换器，其分辨率的限制仅在于可达到的计数器速率和比较器的响应速率。注意切勿把分辨率与精确度混淆。还有一个方法是采用带有分辨率扩展电路的 10 位 A/D 转换器（例如逐次逼近类型的）。这种电路能够以几位的程度增加分辨率，例如从 10 增加到 14 。该电路的框图示于图 30a 。除常规的 10 位 A/D 转换器外，该电路还包含数字至模拟（ D/A ）转换器、减法电路和具有增益 A 的放大器。在 ASIC 或分立电路中， D/A 转换器可与 A/D 组件共享（见图 28 ） 图 30. （ a ）带有 D/A 转换器的分辨率增强电路；（ b ）为过采样而添加人工噪声至输入信号 输入信号 V in 的满量程值为 E ，因此对于一个 10 位转换器，其初始分辨率可表示为 ， （ 28 ） 其单位是每位伏特。例如，对 5V 的满量程， 10 位分辨率是 4.89mV/bit 。首先多路转接器（ MUX ）把输入信号连接至 A/D 转换器，产生用位表示的输出数字值 M 。接下来微处理器输出该值到 D/A 转换器，产生输出模拟电压 V c ，此值是输入信号的近似值。从输入信号电压减去此电压，并由放大器放大得到的值为 （ 29 ） 电压 V D 是实际的输入信号和数字表示的输入信号之间的放大的误差。对满量程输入信号，最大误差（ V in- V c ）等于 A/D 转换器的分辨率，所以对于 10 位转换器， V D=4.89 A mV 。多路转接器把该电压连接至 A/D 转换器，把 V D 转换成数字值 C ： 。 （ 30 ） 因此，微处理器结合了两个数字值： M 和 C ，其中 C 表示高分辨率位。如果 A=255 ，那么对于 5V 的满量程， LSB 19.25 V ，此值相当于 18 位的总分辨率。实际上因为产生于 D/A 转换器、基准电压、放大器偏移、噪声等等的误差，很难达到如此高的分辨率。不过在 12 或 13 位的适度分辨率足以接受时，这种方法还是相当有效的。 另一个扩展分辨率的有效方法基于所谓的过采样。这个主意只有当输入模拟信号在采样点之间发生变化时才会起作用。举例来说，假设 A/D 转换器步长为 50 、 70 、 90mV 等等，当输入信号稳定在 62mV 时，数字数值会给出 70mV ，因而产生 8mV 的数字化误差，过采样也不会带来任何差异。如果输入信号以最大频谱频率 fin 变化，根据奈奎斯特定理（也称为奈奎斯特 - 香农 - 卡特尔定理。该定理指出，最小采样速率必须快至信号最高频率的两倍），采样频率 f s 2 f in 。过采样则需要比奈奎斯特的定义高得多的采样频率。具体可基于下式确定 ， （ 31 ） 其中 n 是扩展位的数值。例如，如果我们有 10 位 A/D ，想要用其产生 12 位（ n=2 ）的数值，采样频率必须至少比 f in 高 16 倍。过采样能够在最高转换频率下改变 A/D 转换的分辨率。因此这个方法适用于转换与 A/D 转换器的最高采样速率比较变化相对较慢的信号。 如上所述，这个方法需要信号在两次采样之间发生变化。如果模拟信号不包含自然变化或固有噪声，可以给输入信号或 A/D 基准电压施加人工噪声，使信号在两次采样之间发生抖动。施加人工噪声的一种实用方法示于图 30b 。微控制器产生脉宽调制（ PWM ）随机脉冲，经电容作平滑处理，然后加至模拟输入信号。抖动的幅度需满足至少为原始分辨率的 0.5 LSB ，不过最好是在大约 2 LSB 。经采样后，为了得到提高的分辨率，增加了来自 A/D 的 的采样，输出结果右移了 n 次。对于上面的例子，增加了 16 个顺序的 10 位数字，右移了 2 次，由此获得 12 位的输出数字。 6 直接数字化 大多数传感器产生低电平信号。为使这些信号达到与数字处理器件兼容的电平，通常需要使用放大器。遗憾的是，放大器和连接电缆或导线会引入附加误差，增加装置的成本，提高复杂性。在基于传感器的系统中，一些新兴趋势引发对信号调节放大器的使用的重新评估（至少对某些换能器是这样）。尤其是很多工业化传感器馈送系统都在利用数字传输和处理设备。这些趋势指向传感器输出的直接数字化，就在传感器之内，这是个艰巨的任务。在考虑传感器单片集成时则更是如此。 传统的 A/D 转换技术强调高电平输入范围。这使得 LSB 步长能够尽可能大，使偏移和噪声误差最小化。出于这个原因，最小 LSB 信号总是选择在至少 100 ～ 200 V 。因此，很多传感器的直接连接，例如 RTD 温度换能器或压阻式应变计，都是不切实际的。在这样的换能器中，满量程（ FS ）输出可能仅限于几个毫伏，这意味着 10 位 A/D 转换器必须有大约 1 V LSB 。 换能器的直接数字化取消了直流增益级，可以在不损失精度的情况下获得更好的性能。直接数字化蕴含的主要思路是把传感器包含在信号转换器中，例如 A/D 转换器或阻抗至频率转换器。所有这类转换器完成的都是调制过程，因而是非线性器件。所以它们由某种非线性电路构成，通常是阈值比较器。比如说偏移阈值电平，就可以调节输出信号，这正是需要的效果。 图 31a 表示一种调制振荡器的简化电路框图。其组成为由运算放大器构建的积分器和阈值电路。电容 C 两端的电压是电流的积分，该电流值则正比于运算放大器同相输入端的电压。当该电压达到阈值时，开关 S W 闭合，因而电容完全放电。直到周期再次重复，电容再次开始对电流积分。放大器的工作点由电阻 R 2 、光电晶体管 S 和基准电压 V ref 确定。入射至晶体管基级的光通量的变化，改变其集电极电流，因而使工作点偏移。类似的电路可用于电阻式换能器（例如热敏电阻）的直接转换。为了提高精度，这种电路可以作进一步改进，比如对放大器的偏移电压或偏置电流及温度漂移等进行补偿。 图 31. 光调制振荡器的简化框图（ a ）和电压（ b ） 7 电容至电压转换器 在很多应用中电容式传感器十分常见。现在，微机械加工技术使得小型单片电容式传感器的制造成为可能。电容式压力换能器利用薄的硅膜片作为可变间隙电容的可移动平板，相对的平板用金属电极制作。这种电容器的本质问题是每单位面积相对低的电容值（大约 ），因此导致大的芯片尺寸。典型的这种器件的零压力电容具有很小的皮法拉量级，因而 10 位分辨率要求电容偏移的检测在 15 fF （飞法拉， 1 飞法拉 = ）或更低的量级。显然任何外部测量电路完全是不可行的，因为连接导线的寄生电容在最好的情况下也有 1pF 的量级：与传感器的电容相比有些太大了。因此要让这样的传感器能够付诸实用的唯一方法，是构建作为传感器自身的集成部分的接口电路。设计这种电路的一个相当有效的方法，是采用开关电容技术。该技术基于由一个电容至另一个电容的电荷转移，利用固态模拟开关实现。 图 32. 微分式电容至电压转换器的简化原理图（ a ）和时序图（ b ） 图 32a 所示为开关电容转换器的简化电路图，其中可变电容 C x 和基准电容 C r 是对称式硅压力传感器的构成部分。单片集成 MOS 开关（ 1 ～ 4 ）由互为反相的时钟脉冲 f 1 和 f 2 驱动。时钟脉冲作用于开关时，电荷出现在公共电容结点。电荷由恒定电压源 V PM 提供，且正比于（ C x- C r ），因而也正比于加至传感器的压力。该电荷加于电荷至电压转换器，其包括运算放大器，积分电容 C f 和 MOS 放电（复位）开关 5 。输出信号是变幅脉冲（图 32b ），可通过通信线路传输，然后或者经解调产生线性信号，或者进一步转换为数字数据。只要积分 OPAM 的开环增益高，输出电压就对寄生输入电容、偏移电压和温度漂移不敏感。最小可测信号（本底噪声）由组件噪声和组件的温度漂移决定。电路分析表明，积分电容 C f 近似等于 OPAM 的频率补偿电容时，达到最小噪声功率。 MOS 复位开关由开态至关态动作时，开关信号由复位晶体管的栅级注入一些电荷至 OPAM 的输入汇总结点（反相输入）。该电荷通过 MOS 晶体管 5 的栅极至沟道电容传输。注入电荷在输出端导致偏移电压。此误差可利用电荷消除器件进行补偿，由此能以高于无补偿电荷幅度两个量级的程度来改善信噪比。 8 集成接口 传感器信号调节的现代趋势，是把放大器、多路复用器、 A/D 转换器及其它电路集成在单个硅芯片中。以下是两个如此集成的例子。图 33 示意一种来自 ZMD 公司的信号调节电路 ZMD21013 。该芯片最适合低电压和低功率多重电阻电桥传感器应用，诸如电池供电的消费类或工业类产品。该集成电路提供可编程的传感器信号的放大和 A/D 转换，带有高达三个电阻电桥，或两个电桥和一个热电偶、热电堆或任何其它低电压发生传感器。应用传感器将只在采样时间内开启，使该电路适合于低功率应用。自动归零、 A/D 分辨率（ 10 位到 16 位）、采样速率、输入范围、灵敏度和测量模式等都可以进行编程。这个电路用于把如下变量的电阻式和电压发生式传感器连接至微控制器时十分有效：加速度、压力、力、流量和温度。 图 33. 集成信号调节器 图 34. 爱普生微控制器的前端 集成接口电路的另一个例子，是爱普生（ EPSON ）的具有超低功耗的 16 位微控制器。其特别适宜于为各类传感器提供接口。图 34 示意其前端具有两个类型的 A/D 转换器：逐次逼近式 10 位 A/D 转换器和带有 24 位计数器的 R/F 转换器。 R/F 转换器适用于监测温度和湿度。这个微控制器具有各种串行接口，能够连接包含在医疗设备中的用于监测体温、血压、身体组分等等的传感器。此外，该产品包含一个分段 LCD 驱动器，用于显示字母符号和图标。该产品还包含一个内置的 MAC （乘法和累加）单元和除法单元，用于传感器信号的高速处理。 R/F 转换器经由一个参考电阻 R ref 工作，该电阻用于设置转换工作点。在转换周期内，电容 C 1 通过电阻式传感器充电，通过 R ref 放电，因而该电容的值及其稳定性对 R/F 转换器的精度没有影响。 9 比率电路 改善传感器精度的一个很有效的方法是比率技术，该技术是最常用的信号调节方法之一。不过需要强调的是，仅在误差源具有相乘特性而不是相加特性时，这个方法才是有用的。即该技术在减小比如热噪声是没用的。另一方面，在解决那些与传感器灵敏度有关的因素，诸如电源的不稳定性、环境温度、湿度、压力、老化的影响等等方面，则是相当有效的。该技术的基本要求是使用两个传感器，一个是作用传感器，对外部激励做出响应，另一个是补偿传感器，对激励屏蔽或不敏感。两个传感器必须暴露于所有其它外部影响之下，这些影响会同时改变它们的性能。必须给通常称为参照的第二个传感器施加参考激励，该激励在产品的使用期限内始终稳定。在很多实际系统中，参照传感器不必与作用传感器完全相同，不过其发生不稳定性的物理特性应该相同。例如，图 35a 表示一个简单的温度探测器，其中作用传感器是负温度系数（ NTC ）热敏电阻 RT 。参考电阻 R 0 在某个参考温度（比如 25 ℃ ）时具有与热敏电阻的电阻值相等的值。两者通过模拟多路复用器连接至带有反馈电阻 R 的放大器。我们假定传感器值有一些漂移，可用时间的函数 a(t) 表示，由此传感器的电阻成为 。电阻 R 0 的特性是其也以同样的函数变化，所以 。由传感器和参照传感器产生的经放大器的输出分别为： 。 （ 32 ） 图 35. （ a ）比率温度探测器；（ b ）电阻值的模拟分压器 可见两个电压是电源电压 E 和电路增益的函数，后者由电阻 R 确定。它们也是漂移 a(t) 的函数。多路复用开关使电压 V N 和 V D 相继出现在放大器输出。如果这些电压馈送至分压器电路，得出的信号可以表示为 ， （ 33 ） 其中 k 是分压器的增益。所以，分压器的输出信号既不受电源电压的影响，也不受放大器增益的影响。其也不会受到双重漂移 a(t) 的影响。该电压仅取决于传感器和其参照电阻。只有在诸如函数 a(t) 、电源或放大器增益这些因素产生的寄生变量不会很快变化时，上述情况才成立。即在多路复用周期内，这些变量不会明显改变。这需要确定多路复用的速率。 比率技术本质上需要采用除法运算。这可以由两个标准方法实现：数字和模拟。数字形式中，来自作用和参照传感器两者的输出信号，经多路复用器，在模拟至数字（ A/D ）转换器中转换为二进制码。随后用计算机或微处理器进行除法运算。在模拟形式中，除法器可以是信号调节器或接口电路的一部分。“除法器”（图 36a ）产生正比于两个输入电压或电流的比值的输出电压或电流： ， （ 34 ） 其中分子表示为 V N ，分母为 V D ，当 V N= V D 时， k 等于输出电压。这些变量的工作范围（工作的象限）由分子和分母的输入及其输出的极性和幅度确定。举例来说，如果 V N 和 V D 两者都是正的或负的，除法器是 1 象限类型的。如果分子是双极性的，除法器为 2 象限类型。通常分母限制在单一极性，因为由一种极性到另一种的转换需要分母过零，这会导致无穷大输出（除非分子也是零）。实际上，分母是来自参照传感器的信号，一般具有相对恒定的值。 图 36. （ a ）除法器的符号；（ b ）作为分母的函数的除法器的增益 除法运算一直是利用模拟电路来实现四种数学运算中最困难的。其难度主要源于除法运算的性质：分母接近零时（分子非零），比值的大小变得相当大，接近无穷大。因此，理想的除法器必须具有潜在的无限大增益和无限大动态范围。对于实际除法器，由于在低值 VD 时漂移和噪声的放大，限制了这两个因素。即对分子来说，除法器的增益反比于分母的值（图 36b ）。因此总误差是几个因素的净影响，诸如增益的分母依赖性，分子，以及类似偏移、噪声和漂移（其必须远小于输入信号的最小值）这样的分母输入误差。此外，除法器的输出在分子和分母的恒定比值时一定是恒定的，与它们的大小无关。例如， 10/10=0.01/0.01=1 ， 1/10=0.001/0.01=0.1 。实际上，一些简单的除法电路使用相当广泛。一个例子是图 35b 中的放大器，其输出信号是电阻比值的函数（注意参考电压 Vr 是负的）： ， （ 35 ） 最常用和最有效的比率电路基于下文阐述的惠斯登电桥设计。 10 差动电路 与相乘干扰相比，相加干扰更为常见，在低电平输出信号时造成严重问题。考虑一个热电传感器的例子（图37a），其中热流感应陶瓷片由内部金属壳承载。因为热电性同时也是压电性的，除了热流，该传感器还易于受到机械应力干扰。即使轻微的振动也会产生寄生压电信号，而且其幅度可能高于热电电流几个量级。解决办法是制造带有淀积在同一陶瓷衬底上的双电极的传感器，如图37b所示。本质上这是在同一陶瓷片上创建两个完全相同的传感器。两个传感器几乎同样地对所有激励作出响应。因为它们的连接相反，假定来自其中一个传感器的 V pyro和 V piezo分别与来自另一个传感器的相等，导致输出电压基本为零： (36) 如果阻止其中一个传感器接收热辐射（ V pyro2=0），则 V out= V pyro1。换句话说，幸亏有减法运算（ V piezo1= V piezo2）使彼此互相抵消了，这个组合传感器就对压电效应不敏感了。传感器制造的差动方法是一种对称形式，且连接至对称接口电路（如差动放大器），两个信号彼此相减，因而是减小噪声和漂移的十分有效的方法。不过这个方法仅当双传感器完全对称时有效。非对称性将按比例减小噪声消除的作用。举例来说，如果非对称性是5%，噪声的消除不会大于95%。 图37. (a)封装在一个金属壳内的双热电传感器； (b)淀积在热电平板两面的金属电极；(c)双组件的等效电路 11 电桥电路 11.1 一般概念 惠斯登电桥电路很常见，能够很有效地应用于传感器级的比率技术（除法技术）。其基本电路示于图38。阻抗Z可以是有源的或无源的，即其可以是简单的电阻，如压阻式应变计，或是电容，或是电感，或几种的组合。对于纯电阻，阻抗为R，对于理想电容器，其阻抗的大小等于 ，对于电感，则为 ，其中f是流过元件的电流的频率。电桥输出电压由下式表示 ， （37） 满足下列条件时，即认为电桥处于平衡状态： 。 （38） 图38. 惠斯登电桥的一般电路 在平衡条件下，输出电压为零。当电桥中的至少一个阻抗变化，电桥失去平衡，输出电压出现正向或负向变化，取决于阻抗变化的方向。要确定电桥相对于每个阻抗的敏感度，可由公式（37）求偏微分得出： ( 39） 把这些公式相加，我们得到电桥的敏感度： ， （40） 对（40）式仔细审视可知，为了实现比率补偿（比如温度稳定性、漂移等），仅需相邻的阻抗对（即 Z 1 和 Z 2， Z 3 和 Z 4）完全相同。需要注意的是，平衡电桥中的阻抗不必一定相等，只要比例平衡（38）能 够满足即可。在很多实际电路中，只有一个阻抗被用于传感器，从而若 Z 1 是传感器，电桥敏感度成为 。 （41） 电阻式电桥电路常用于应变计、压阻式压力传感器、热敏电阻温度计、湿敏电阻器，以及其它需要抵 抗环境因素影响的传感器。用于测量力、位移、湿度等等的电容性和磁性传感器也采用类似的做法。 11.2 非平衡电桥 基本的惠斯登电桥电路（图39a）通常工作于非平衡电桥。这称为测量的偏移法。该方法基于电桥对 角线电压的检测。电桥输出电压是不平衡度 Δ 的非线性函数，这里传感器的电阻 。不过对于很 小的变化（ Δ < 0.05），电桥的输出可以认为是准线性的，通常都会是这种情况。在 R 1= R 2 和 R 3=R 时达到 电桥最大灵敏度。当 R R 2 或 R R 1 时，电桥输出电压下降。假定k= R 1/ R 2，电桥灵敏度可表示为： （42） 图39. 采用电桥电路的两种方法：（a）非平衡电桥；（b）带有反馈控制的零位平衡电桥 图40. 作为阻抗比例的函数的非平衡电桥的灵敏度 据此公式计算得出的归一化曲线图见图40。图中表明在k=1 时达到最大灵敏度，不过在0.5 < k < 2 的范围内灵敏度下降相对较小。如果用电流源反馈至电桥，而不是电压源，在小的 Δ 和单一变量时，其输 出电压表示为 ， （43） 其中i是激发电流。 11.3 零位平衡电桥 利用电桥电路的另一种方法称为零位平衡。该方法克服了为达到好的线性度电桥臂中只能有小变化（Δ ）的限制。零位平衡的基本要求是电桥始终保持在平衡状态。要满足电桥平衡（37）的要求，电桥的另一个臂需要与感应臂一同变化。图39b说明了这个概念。一个控制电路按照来自误差放大器的要求调节 R 3的值。传感器的输出电压可以从平衡臂 R 3的控制信号获得。例如 R v和 R 3两者可以都是光敏电阻。光敏电阻 R 3可以通过由误差放大器控制的发光二极管（LED）实现连接。流过LED的电流成为电阻 R v的测量，因而也是对由传感器探测到的光强度的测量。 11.4 电桥放大器 用于电阻式传感器的电桥放大器或许是最常用的传感器接口电路。这些电路可以有各种配置，取决于所需的电桥接地和有效的接地参考电压或浮点参考电压。图41a表示所谓的有源电桥，其中的可变电阻（传感器）是浮动的，即与地隔离，并接入OPAM的反馈回路。如果电阻式传感器的传递函数可用一阶函数建模： ， （44） 其中 α 是输入激励，此电路的传递函数为 。 （45） 图 41. 运算放大器至电阻式电桥电路（非平衡模式）的连接 具有 浮点电桥 和浮点参考电压源 V 的电路示于图 41b 。此电路可提供由反馈电阻（其值为 n R 0 ）确定的增益： 。 （ 46 ） 具有非对称电阻（ R ≠ R 0 ）的电桥可以用于图 41c 所示的电路。该电路需要浮点参考电压源 V ： （ 47 ） 当电阻式传感器接地且来自接口电路的增益合适时，可采用图 41d 所示的原理图。其传递函数由下式确定 （ 48 ） 要注意此电路可能包含平衡电位计，其电阻分区会包括在相应的电桥臂之中。电位计用于调节电桥元件的容差，或通过一些固定偏压补偿电桥的平衡。电桥完全平衡时，其输出电压 V out 等于电桥激发电压 +V 的二分之一。为了更好地利用运算放大器开环增益， n 的值不应超过 100 。 12 数据传输 来自传感器的信号可能要以数字或模拟的格式传输至系统的接收端。大多数情况下，数字格式显然需要在传感器处使用模拟至数字转换器。以数字格式传输有几个优点，其中最重要的是抗干扰性。因为数字信息的传输超出了本书的范围，我们不作进一步的讨论。不过在很多情况下，由于某些原因，无法进行数字传输。此时传感器的输出信号以模拟形式传输至接收位置。取决于连接，传输方法可分为 2 、 4 和 6 线制方法。 12.1 二线制传输 在制造工业中，二线制模拟发送器用于连接传感器至控制和监测器件。例如在制造工序中要测量温度时，二线制发送器传递该测量信号至控制室或把模拟信号直接连接至工序控制器。两条导线可用于传输电压或电流，不过工业标准上采用的是电流。导线携带的电流在 4 到 20mA 范围之间变化，表示输入激励的整个范围。零激励对应于 4mA ，最大值则对应于 20mA 。采用电流而不是电压有两个优点，如图 42 中所表明的。两根导线连接控制器位置至传感器位置。在传感器一侧，传感器连接至所谓的二线制发送器。该发送器可以是一个电压至电流转换器。即把传感器信号转换为变化的电流。在控制器一侧，有可提供高至 20mA 电流的电压源。两条导线形成电流回路，回路的传感器一侧是传感器和发送器，而在控制器一侧是以串联方式连接的负载电阻和电源。传感器信号发生变化时，发送器的输出电阻发生相应变化，因而在 4 和 20mA 之间的范围调节电流。携带了信息的相同电流，也用于为发送器和传感器提供工作电源。显然，即使在产生 4mA 电流的最低输出信号时，其产生的电压也必须足以为回路的发送器一侧提供电源。回路电流形成控制侧负载电阻端的压降。此电压即接收到的信号，适合于电子电路的进一步处理。二线制方法的一个优点是，传输电流不受连接导线电阻的影响（只要其不发生变化），因而也不受传输导线长度的影响，当然这是有限度的。 12.2 四线制 传感 有时需要把电阻式传感器连接至位于远处的接口电路。当这种传感器具有相对较低的电阻时（例如压敏电阻或 R TD 通常具有 100 量级的阻值），连线电阻就会造成严重问题，因为其改变了加于传感器的激发电压。这个问题可通过所谓的 4 线制方法（图 43a ）解决。该方法能够在不必考虑连接导线电阻的情况下测量远处电阻的阻值。作为测量的主体，传感器通过四条而不是两条导线连接至接口电路。两条线连接至电流源，另外两条线连接至电压计或放大器。恒流源（电流泵）具有很高的输出电阻，因此其通过回路推送的电流几乎与回路中的电阻 r 无关。电压计或放大器的输入阻抗很高，因此没有电流从电流回路分流至电压计。电阻 R x 两端的压降为 ， （ 49 ） 与任何连线电阻 r 无关。 4 线制方法是测量远距离探测器电阻的非常有效的手段，相当广泛地应用于工业和科研领域。 图 42. 二线制 20mA 模拟数据传输 图 43. （ a ）远距离测量电阻的四线制方法；（ b ）电桥的六线制测量 12.3 六线制 传感 当惠斯登电桥电路位于远处时，电桥的端电压在电桥的温度稳定性方面发挥着重要作用。该电压通常是测量电压或控制电压。长距离传输导线可能引入与电桥激发电压相串联的不可接受的高电阻，干扰温度补偿。此问题可通过配置两条额外的馈送电压至电桥的导线解决，这样能够利用两条导线来测量电桥的端压（图 43b ）。加于电桥的实际激发电压和电桥的差分输出电压，由具有可忽略的小输入电流的高输入阻抗的电压计测量。由此在数据处理端获得精确的电桥电压，且不受长距离传输线路的影响。

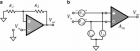
译者：穆心 译注：本文为《现代传感器手册（第四版）》一书英文版第五章的中文翻译，分三部分发出。译者出于学习和了解的目的翻译该文，同时也希望向同业就教，旨在厘清概念，夯实基础，启迪思维，促进创新。传感器可以千变万化，理论基础则万变不离其宗。而作为能够广泛应用的产品，又离不开具有创新精神的企业多年锲而不舍的精心研制和打磨。所以成功的企业，不只是创新基因强大，还必定是在诸多细节上不断积累自己的优势。制造设备可以一样，制造工艺可以大同小异，最终被市场所接受的，必定是那些具有优良性价比的产品。通过本文，可以对如何在具体的细节上改进产品窥知一二，进而举一反三。译者也希望借此能把个人爱好和个人的专业背景，与促进传感器产业的发展达成些微的联系；能够以绵薄之力，对从事或有志于从事研发制造传感器的工程技术人员及学生提供些微帮助。 原书名：《现代传感器手册——原理、设计和应用》，第四版， 2010 年；作者：雅各布•弗瑞登（ Jacob Fraden ）。 1 接口电路的输入特性 系统设计者很难把传感器直接连接到处理、监测或记录装置上，除非传感器带有内置的具有合适输出格式的电路。传感器产生的电信号常常是太弱，或太多噪声，或包含不需要的成份。此外，传感器的输出可能与数据采集系统的输入要求不匹配，即可能具有不适当的输出格式。为了使传感器与处理器件匹配，它们或者必须分享“共同值”，或者在其间需要有某种“配对”部件。换句话说，来自传感器的信号在输入处理器件（负载）之前，通常需要调节。这里提到的负载通常需要电压或电流作为其输入信号。 接口电路或信号调节电路具有特定目的：把来自传感器的信号变成与负载器件相匹配的格式。图 1 表示激励作用于传感器，传感器则通过接口电路连接至负载。为了有效地发挥作用，接口电路必须是两个主人的忠实奴仆：传感器和负载器件。其输入特性必须与传感器的输出特性匹配，其输出必须可连接至负载。我们关注的是传感器，所以下面我们将只讨论接口电路的前置部分。此外我们将讨论一些典型的有源传感器所需的激发电路，即用于那些需要电信号才能产生电输出的传感器的电路。 图 1. 接口电路匹配传感器和负载器件的信号格式 接口电路的输入部分可以通过几个标准数值加以规定。这些数值对计算该电路能如何精确地处理传感器的输出信号，以及该电路在总误差分配中占有多大份额，都是有用的。 输入阻抗表示传感器的电路负载有多大。阻抗可用复数形式表示为： ， （ 1 ） 其中 V 和 I 是施加于输入阻抗的电压和电流的复数表示。例如，如果电路的输入模型化为输入电阻 R 和输入电容 C 的并联（图 2a ），则其复数输入阻抗可表示为 ， （ 2 ） 其中 是角频率， j= 是虚数单位。在很低频率时，具有相对较低的输入电容和电阻的电路，其输入阻抗几乎等于输入电阻： 。所谓相对较低，这里意味着上公式的电抗部分较小，即下式成立： 。 （ 3 ） 图 2. （ a ）接口电路的复数输入阻抗；（ b ）电压生成传感器的等效电路 考虑电路的输入阻抗时，必须同时考虑传感器的输出阻抗。例如，如果传感器具有电容性质，要确定输入级的频率响应，传感器的电容必须以并联方式与电路的输入电容相连。公式（ 2 ）提示，输入阻抗是信号频率的函数。随着信号变化速率的增加，输入阻抗减小。 图 2b 表示一种电压生成传感器的等效电路。该电路由传感器的输出阻抗 Z out 和电路的输入阻抗 Z in 构成。来自传感器的输出信号用电压源 e 表示，其以串联的形式与传感器的输出阻抗相连。除电压源外，对某些传感器，把其输出信号表示为来自电流源则更为方便，这时需要以并联的方式与传感器输出阻抗连接。两种表示方法互相等效，所以我们采用电压形式。考虑到两者的阻抗，电路输入电压 Vin 表示为 。 （ 4 ） 在一些特定情况下，需要对传感器的等效电路给以定义。这有助于分析传感器—接口电路组合的频率响应和相位滞后。例如，电容式探测器可模型化为以并联方式与输入阻抗连接的纯电容。另一个例子是压电式传感器，其可以表示为带有分流电容（大约 10pF ）的阻值很高的电阻（大约 ）。 为了说明输入阻抗特性的重要性，让我们考虑一个连接于输入阻抗的纯电阻式传感器，如图 2 所示。作为频率 f 的函数的电路输入电压可以由下式表示 （ 5 ） 其中 是转折频率（即振幅下降 3dB 时的频率）。如果我们假定振幅检测时需要 1% 的精确度，那么我们就可以计算出电路能够处理的最大激励频率： ， （ 6 ） 或者 ；也就是说必须如此选择阻抗，才能确保足够高的转折频率。例如，如果激励的最高频率是 100Hz ，转折频率必须选择为至少 700Hz 。实际上， fc 要选择得更高些，因为后续电路中还有额外的频率限制。 不能忽略接口电路的前置电路的响应速度。最常用于接口电路构建模块的运算放大器，通常具有有限的频带宽度。有所谓的可编程运算放大器，能让使用者控制（编程）偏置电流，从而控制前置电路的频率响应。电流越大，响应就越快。 图 3. 输入级电噪声源的等效电路 图 3 是一种接口电路输入特性的更详细的等效电路，例如放大器或 A/D 转换器。该电路表征为输入阻抗 Zin 和几个发生器。这些发生器表示由电路自身产生的电压和电流。这些信号是寄生的，如果不妥善处理，可能会造成严重的问题。所有这些干扰信号都与温度有关。 电压 e0 称为输入偏移电压。如果电路的输入端短路，该电压会冒充存在一个具有 e0 的值的输入 dc 信号。需要注意的是，偏移电压源与输入串联，其导致的误差与传感器的输出阻抗无关。 输入偏置电流 i0 也是由电路产生的。对于很多双极型晶体管来说，其值相当高，对于结型场效应管则很小， CMOS 电路就更小。当电路或传感器用在高阻抗器件时，这个电流可能会带来严重问题。偏置电流流过电路的输入阻抗和传感器的输出阻抗，导致寄生的压降。该电压可能会达到能造成影响的量级。例如，如果一个压电式传感器连接到具有 （ ）输入电阻的电路，输入偏置电流为 1nA （ ），输入端的压降即等于 ，这的确是很高的值。与偏移电压相比，偏置电流导致的误差正比于传感器的输出阻抗。对于具有低输出阻抗的传感器，该误差小到可以忽略。例如，电感式检测器就对偏置电流的大小或变化不敏感。 用于高阻抗电路时，电路板的漏电流可能成为误差的来源。该电流可能是印刷电路板（ PCB ）中的较差的表面电阻导致的。产生的原因可能是：质量低劣的 PCB 材料，焊剂残渣造成的表面污染（清洁不良的电路板），潮湿，失效的保护涂层。图 4a 表示电源总线和板电阻 RL 可以导致通过传感器输出阻抗的漏电流 iL 。如果传感器是电容性的，其输出电容会被漏电流快速充电。这不仅会导致误差，甚至还会导致传感器损坏，特别是当传感器用于一些化学混合物时（比如电阻式湿度传感器）。 已知有几种技术可使电路板漏电流最小化。一种是仔细安排电路板布局，使高电压导体避开高阻抗器件。在多层电路板中经厚度方向的漏电也不容忽视。另一种方法是电气防护，这是一种老方法了。所谓的有源屏蔽也很有效。其做法是用连接到与输入具有相同电势的低阻抗点的导电线路覆盖输入电路。这种防护装置从电路板的其它点吸收漏电流，极大减少了可能到达输入端的电流。要彻底消除漏电流，需要在印刷电路板两面都有防护环路。举例来说，放大器就带有防护环路，由放大器反相输入的相对较低阻抗驱动。 图 4. （ a ）电路板漏电影响输入级；（ b ）输入级的有源屏蔽 十分可取的做法是把高阻抗接口电路置于尽可能靠近传感器的位置。然而有时连接线是无法避免的。这时推荐采用具有良好绝缘的同轴屏蔽电缆。对于关键应用，聚乙烯或高级纯（未经改性的）特氟龙是最佳选择。除了潜在的绝缘问题外，甚至短的布线也会在高内阻时导致无法接受的带宽下降。这些问题通过改善电线屏蔽即可在很大程度上避免。图 4b 表示连接于放大器反相输入端的电压跟随器。跟随器驱动电线的屏蔽，从而减小因电线弯曲导致的电线的电容、漏电流和寄生电压。跟随器同相输入端的小电容改善了其稳定性。 必须避免的另一个问题，是把除了传感器以外的、有可能导致问题的器件连接至放大器的输入端。这种“麻烦制造者”的一个例子是陶瓷电容器。希望滤除输入端的高频传输噪声时，设计者往往在输入端或输入级的反馈电路中采用滤波电容器。如果出于节约成本或节省空间的原因选用了陶瓷电容器，就会带来不希望出现的麻烦。很多电容器具有所谓的电介质吸收特性，表现为一种记忆效应。如果这种电容器承受来自传感器或电源、或只是来自任何外部噪声源的尖峰电荷，该电荷就会改变电容器的介电特性，让电容器此时变得像个小电池。这个“电池”或许会花很长时间才会耗尽其电荷：从几秒到数小时。由此“电池”产生的电压被加至传感器的信号，有可能导致明显的误差。如果在输入级必须使用电容器，应该采用薄膜电容器，而不是陶瓷电容器。 2 放大器 大多数无源传感器只产生微弱的输出信号。这些信号的大小可能在微伏（ V ）或微微安（ pA ）的量级。换句话说，标准的电子数据处理器，诸如 A/D 转换器、调频器、数据记录器等等，需要伏特（ V ）和毫安（ mA ）这样的量级相当大的输入信号。因此需要把传感器输出信号进行放大，电压增益需高至 10,000 ，电流增益需高至 1 百万。放大是信号调节的一部分。有几种标准配置的放大器，可用于放大来自各种传感器的信号。这些放大器可由分立元器件构成，诸如半导体器件、电阻、电容和电感。作为另一种选择，放大器也常常由标准构建模块组成，诸如运算放大器和各种分立元器件。 需要清楚了解的是，放大器的用途十分广泛，不只限于增加信号大小。放大器也可以是阻抗匹配器件，信噪比增强器，滤波器，以及输入和输出之间的隔离器。 2.1 运算放大器 放大器的基本构建模块之一，是所谓的运算放大器（ OPAM ），其可以是集成型（单片电路）或混合型（由单片电路和分立器件组成）电路。集成 OPAM 可以包含数百个晶体管以及电阻和电容。通过在 OPAM 周边配置分立元件（电阻、电容、电感等），模拟电路设计者可以创建无数种有用电路，不仅仅是放大器，还可以有很多其它类型的电路。运算放大器也可用于模拟或混合技术类型的定制集成电路的构成单元。这些电路被称为专用集成电路，缩写为 ASIC 。下面我们将介绍一些采用 OPAM 的典型电路，这些电路经常使用于连接各种传感器。 作为构建模块，好的运算放大器具有如下性能（ OPAM 原理图表示见图 5 ）： Ÿ 双输入：一个反相（ - ），一个同相（ + ）； Ÿ 高输入电阻（数百 M 甚至 G 的量级）； Ÿ 低输出电阻（零点几 ）； Ÿ 具有驱动电容负载的能力； Ÿ 低的输入偏移电压 e0 （几个 mV 甚至 V ）； Ÿ 低的输入偏置电流 i0 （几个 pA 甚至更低）； Ÿ 很高的开环增益 （至少 ，最好是超过 ）。即 OPAM 必须能够以 为因数，增大（放大）其两个输入之间的电势差 Vin ； Ÿ 高共模抑制比（ CMRR ）。即放大器抑制施加于其两个输入端的同相等幅输入信号（共模信号） VCM ； Ÿ 低的固有噪声； Ÿ 宽的工作频率范围； Ÿ 对电源电压的变化敏感性低； Ÿ 其自身特性具有高的环境稳定性。 关于详细信息和应用指南，使用者可参考相应制造商出版的数据手册和商品目录。这样的商品目录通常包括关于 OPAM 的每个重要特性的选择指南。例如， OPAM 按照诸如低偏移电压、低偏置电流、低噪声、带宽等等标准进行分级。 图 5. （ a ）运算放大器的通用符号；（ b ） OPAM 的增益 / 频率特性 图 5a 表示没有任何反馈组件的运算放大器。所以其工作在所谓的开环状态。 OPAM 的开环增益 总是标明的，但其并不是一个很稳定的参数。其与频率的关系可以用图 5b 近似表示。 AOL 随负载电阻、温度和电源波动而变化。很多放大器具有 0.2 至 1%/ ℃ 量级的开环增益温度系数，以及 1%/V 量级的电源增益敏感性。 OPAM 很少用于开环（没有反馈组件），因为高的开环增益会导致电路失稳，以及大的温度漂移、噪声等等。例如，如果开环增益是 ， 10 V 输入电压的偏移可导致大约 1V 的输出偏移。 OPAM 放大小幅高频信号的能力由增益带宽乘积（ GBW ）指定，其值等于放大器增益为一时的频率 f1 。换句话说，高于 f1 频率时，放大器则无法放大。图 6a 表示同相放大器，其中电阻 R1 和 R2 构成反馈回路。此时的增益 A=1+R2/R1 是闭环增益。其在相当宽的频率范围都可看作常数（见图 5b ），然而不管是否有反馈， f1 都是频率限制因子。线性度、增益稳定性、输出阻抗和增益精度都可以通过反馈深度加以改善，且这时主要取决于反馈组件的特性。作为适度精度的一般原则，在所关注的最高频率， OPAM 的开环增益应该大于其闭环增益的 100 倍。对于更高的频率，开、闭环增益比值应该为 1,000 或更大。 图 6. （ a ）同相放大器；（ b ）用连接于运算放大器输入端的发生源表示其偏移电压和偏置电流 OPAM 的典型数据手册指定偏置和偏移电压。由于制造技术的限制，任何 OPAM 不仅是个纯放大器，而且会是个可能与输入相关的电压和电流的发生器（图 6b ）。因为这些寄生信号实际上施加于输入端，就与有用信号一起被放大了。 由于偏移电压和偏置电流，当施加零输入信号时，接口电路并不产生零输出。在直流耦合电路中，这些不良输入信号可能无法与有用信号区别开来。如果在所需精度下输入偏移电压仍然很大，可以由放大器直接将其消除（如果放大器具有消除端），或者采用单独的偏移补偿电路消除。 应用工程师会关注输出偏移电压，其可由下式导出： （ 7 ） 其中 Reqv 是输入端的等效电阻（传感器的输出电阻和放大器的输入电阻的结合）， e0 是输入偏移电压， i0 是输入偏置电流。偏移与温度有关。在放大器具有高增益的电路中，输出电压偏移会是明显误差的来源。有几种方法来解决这个问题。其中一个方法是选择具有低偏置电流、高输入电阻和低偏移电压的放大器。斩波稳定式放大器对减小偏移电压有特殊效果。 2.2 电压跟随器 电压跟随器（图 7 ）是一种提供阻抗由高至低转换的电路。典型的跟随器具有高输入阻抗（高输入电阻和低输入电容）和低输出电阻（输出电容无差别）。好的跟随器具有十分接近于一（较低频率时的典型值为 0.999 ）的电压增益和高电流增益。本质上它是个电流放大器和阻抗转换器。其高输入阻抗和低输出阻抗，使其在许多传感器和信号处理器件之间起到不可或缺的连接作用。 连接于传感器时，跟随器对其性能的影响很小，由此在传感器和负载之间提供缓冲作用。设计跟随器时，以下这些技巧或许是有用的： Ÿ 对于产生电流的传感器，跟随器的输入偏置电流必须小于传感器的电流至少 100 倍。 Ÿ 输入偏移电压必须或者可以微调，或者小于要求的最低有效位（ LSB ）。 Ÿ 偏置电流和偏移电压的温度系数应该在整个温度范围区间不会导致大于 1LSB 的误差。 图 7. 采用运算放大器的电压跟随器 2.3 测量放大器 测量放大器（ IA ）具有两个输入和一个输出（图 8 ）。其与运算放大器的区别在于它的有限增益（通常不大于 100 ）和连接至信号源时其两个输入的可用性。后一个特性意味着所有需要的反馈组件连接至测量放大器的其它部分，而不是其同相和反相输入。 IA 的主要功能是产生一个正比于其两个输入之间电压差的输出信号： ， （ 8 ） 其中 V+ 和 V- 分别为同相和反相输入端的输入电压， a 是增益。确保两个输入端具有高的输入电阻很重要，以便放大器能够用于真正的差分形式。放大器的差分输入对于抑制具有相加性质的共模干扰十分重要。因此 IA 应具备高的共模抑制比（ CMRR ），即其输出信号应该对 V+ 或 V- 的值不敏感，但只对两者的差异做出反应。 测量放大器可以用几个独立的 OPAM 以单片或混合的形式构建。现在，测量放大器已经可以由很多制造商以单片电路的形式提供。一个高质量的单片测量放大器的例子是由德州仪器公司制造的 INA118 。该放大器具有 50 V 的低偏移电压（当两个输入端连在一起时这款 IA 产生的输出信号）和高的 CMRR （ 110dB ）。增益由单一电阻设置。同样，许多集成电路，诸如微控制器或 DSP （数字信号处理器），都有内置的、作为输入传感器和内部 A/D （模拟至数字）转换器之间直接接口的输入测量放大器。 图 8. 测量放大器 2.4 电荷放大器 电荷放大器（ CA ）是一类十分特殊的电路，其必须有极低的偏置电流。这类电路用于把来自电容式传感器、量子探测器、热电传感器和其它器件的信号转换为电压信号，这些器件产生很小的电荷（微微库仑量级， pC ）或电流（微微安量级）。电荷至电压转换器的基本电路示于图 9a 。电容 C 接入 OPAM 的反馈网络。其漏电阻 r 必须明显大于最低工作频率时电容的阻抗。通常推荐采用优质薄膜电容，同时采用优质印刷电路板，其上组件用保形涂层涂覆。 此转换器的传递函数为 。 （ 9 ） 对于精密应用，可以选择专门集成电荷感应前置放大器的商业化产品。 很多传感器可被模型化为电容。一些电容式传感器是有源的，即它们需要激发电路。例如麦克风、电容式力学和压力传感器，以及湿度探测器。其它电容式传感器是无源的，即可直接把激励转换成电荷或电流。例如压电式和热电式探测器。也有非电容式传感器可视为电流发生器。一个例子是光电二极管。 图 9. 电荷至电压（ a ）和电流至电压（ b ）转换器 图 10. 电流产生传感器的等效电路 电流产生传感器模型化为漏电阻 r 与具有无限高内阻的电流源并联（图 10 ）。传感器产生电流 i ，其有两个路径流出：一个是通过传感器漏电阻 r 的电流 i0 ，另一个是流向接口电路输入阻抗 ZL 的电流 iout 。显然电流 i0 是无用的，要使电流至电压转换的误差最小化，传感器的漏电阻必须远大于接口电路的阻抗（图 11 ）。 图 11. 同相电流至电压转换器 欧姆定律提示，要把电流 iout 转换成电压，电流要通过一个合适的阻抗，该阻抗两端的压降要正比于电流的幅度。图 9b 表示一个基本的电流至电压转换器，其中电流发生传感器连接至作为虚拟地的 OPAM 的反相输入。换句话说，反相输入端的电压几乎等于接地的同相输入端电压。传感器在其输出端接近于零电压状态工作，其电流决定了 OPAM 的输出电压： （ 10 ） 图 12. 电阻倍增器（ a ）和（ b ） 为了电路的稳定性，通常需要有 r << R 的电阻，因为在高频时，如果没有这样的电阻， OPAM 会工作于接近开环增益状态，有可能导致振荡。若传感器不具有小内阻就更需注意。虚拟接地的优点是输出信号与传感器的电容无关。该电路产生在相位上相对于电流偏转 180 ° 的电压。示于图 12a 的同相电路能够转换和放大这样的信号，然而其速度响应取决于传感器的电容和转换电阻 R1 两者。因此，对阶跃函数的时域响应可表示为 。 （ 11 ） 当转换电流来自压电式和热电式这样的传感器时，电阻 Rb （图 9b 中的 R ）可能需要有数十或数百吉欧的量级。在很多情况下，这么高阻值的电阻也许不易获得，或者由于差的环境稳定性而无法使用。高阻值电阻可由电路来模拟，被称为电阻倍增器。通过在放大器的正输入端采用该放大器的正反馈配置来实现。图 12a 表示用 R1 和 R3 形成电阻分压器。由于 OPAM 的高开环增益，在同相和反相输入端的电压几乎相等： 。由此分压器的电压 V2 为 ， （ 12 ） 流过电阻的电流通过压降确定： 。 （ 13 ） 由此公式，可得出作为输入电流和电阻回路的函数的输入电压： 。 （ 14 ） 可见电阻 Rb 增加了倍增因子 （ 1+R3/R1 ） 。举例来说，如果你能够考虑的最高阻值是 10 ，通过选择插入比如说是 5 的倍增因子，就可以得到 50 的等效电阻。作为一种有效的技巧，必须慎重使用电阻倍增。显然，噪声、偏置电流和偏移电压，所有这些也都会以同样的因子（ 1+R3/R1 ）倍增，在一些应用中这或许是不可接受的。加之，因为回路形成正反馈，有可能引发电路不稳定。因此在实际电路中，电阻倍增应当限制在因子 10 以内。如果放大器的负输入端需要电阻倍增，图 12b 的电路是现成可用的。电阻倍增的推导与公式（ 14 ）相同。 3 光至电压转换器 光至电压转换器基于光电传感器和电流至电压转换电路的组合。为了检测典型情况为一或几个光子的极低强度的光，通常使用光电倍增管，然而在要求不高的应用中，可采用三种类型的光电传感器：光电二极管、光电晶体管和光敏电阻。它们利用了爱因斯坦发现的光电效应，这为其赢得了诺贝尔奖。光电二极管和光电晶体管的区别在于半导体芯片的结构。光电二极管有一个 p-n 结，而光电晶体管有两个 p-n 结，晶体管的基级可能是空置的，也可能具有独立的端子。基级电流是光感应电流，经晶体管的 b 放大后产生集电极电流。因此光电晶体管相当于内置电流放大器的光电二极管。 图 13. （ a ）光电二极管的等效电路；（ b ）与电流至电压转换器连接的 反相偏置的光电二极管；（ c ）电路的负载曲线 从电的角度来看，光电二极管可表示为如图 13a 所示的等效电路。其包括一个电流源（内输入阻抗无限大），一个并联的常规二极管（如同整流二极管），结电阻 Rj ，结电容 Cj 和串联电阻 Rs 。电流源产生正比于光通量的光电流。该电流以光电二极管的负极（ - ）至正极（ + ）的方向流过。注意在很强的光照下，光电流将开始通过非线性整流二极管流动，这会使线性度变差。 光电二极管可用于伏打或电流模式。伏打模式中，光电二极管连接至极高的电阻（ ）和优质电压放大器。此时二极管的作用就像电池，其电压正比于光强度。该电压是光电流 ip 通过内部结电阻 Rj 产生的。而在电流模式中，光电二极管实际上是短路的（二极管两端电压为零），电流 ip 被导向电流至电压转换器，如下文的解释。这种节点连接很常用，特别是需要高速响应的应用。 图 14. （ a ）带有电流至电压转换器的零偏置光电二极管；（ b ）传递函数图示 图 15. （ a ）采用光电晶体管的光至电压转换器；（ b ）传递函数图示 采用运算放大器的电路示于图 13b 。注意参考电压 Vr 在光电二极管两端产生一个恒定的反向偏压。图 13c 表示具有负载电阻 R 的工作点。采用反向偏压光电二极管的电路具有高速响应和宽比例范围输出的特性。因而此电路被广泛使用。另一种采用运算放大器的电路是在光电二极管两端施加零偏置，如图 14a 所示。这种配置在宽的工作范围内提供接近理想的短路电流。输出电压（ Vout ）由 Vout=ipR 给定。图 14b 表示输出电压与辐射强度之间的关系（传递函数）。给光电二极管提供无偏置和高阻抗负载的配置，减少了暗电流的影响，增加了与辐射强度相关的光电流的线性范围。需要注意的是，在相当小的光照下要得到有效的输出（几百毫伏），电阻 R 的值要相当大，达到 100 甚至几个 的量级。如果找不到这样的电阻，可以谨慎采用图 12c 中所示的电阻倍增电路。倍增因子不应大于 10 ，因为电路中所有不好的因素都会倍增：偏移电压、偏置电流，以及噪声。使用高欧姆电阻时，光电传感器和接口电路需要做电气屏蔽。即使环境与这种电阻的微小电容耦合，也会带来很多干扰，特别是来自电源线（ 60 或 50Hz ）的干扰。 用于光电晶体管的接口电路是类似的，除了其集电极 - 发射极端子之间需要施加电压，如图 15a 所示。该电路的传递函数示于图 15b 。光电晶体管电路对光敏感得多，但代价是强光照时较高的非线性。 这里我们没有叙述用于光敏电阻的接口电路，因为任何合适的电阻测量电路都能用于此目的。一个例子是惠斯通电桥电路，我们将在下面讨论这种电路。 4 激发电路 有源传感器的工作需要外部电源。例如温度传感器（热敏电阻和 RTD ）、压力传感器（压电式和电容式），以及位移（电磁式和电阻式）。电源可用不同形式施加于传感器。可以是恒压、恒流，以及正弦或脉冲电流。甚至可以用光或电离辐射的形式提供。这种外部电源叫作激发信号。在很多情况下，稳定和精确的激发信号直接与传感器的精度和稳定性相关。因此，产生具有所需精度的信号，使传感系统的整体性能不会变差就十分必要。下面我们评述几种向传感器馈送合适的激发信号的电路。 4.1 电流发生器 电流发生器常用于以预先确定的电流馈送至传感器的激发电路，该电流在一定范围内与传感器特性、激励值或环境因素无关。一般来说，电流发生器（电流泵）是一种产生的电流与负载阻抗无关的装置。即在发生器的能力范围内，其输出电流的大小必须基本上保持与负载阻抗的任何变化无关。也就是说理想的电流源（发生器）具有无限高的输出电阻，因而任何串联的负载值不会导致任何改变。向变化的负载提供电流时，根据欧姆定律，相应的电压必须同步改变。 电流发生器能够用于传感器接口，在于其产生精确控制大小和形状的激发电流的能力。因此电流发生器不仅要产生与负载无关的电流，而且还必须能够由外部信号源（波形发生器）进行控制，在大多数情况下这种信号源具有电压输出。好的电流发生器必须能够产生以高保真度跟随控制信号，且在宽的阻抗范围与负载无关的电流。 电流发生器有两个主要特性：输出电阻和电压裕度。输出电阻要按实际情况尽可能的高。电压裕度则是在不影响输出电流情况下负载端能够达到的最高电压。对于高电阻负载，根据欧姆定律，一个给定的电流需要较高电压。例如，如果所需激发电流为 i=10mA ，在任何给定频率下最高负载阻抗为 ZL=10 ，则需要至少 iZL=100V 的电压裕度。下面我们来了解一些有用的电路，这些电路在电压裕度增大时，其输出电流仍然能够由外部信号控制。 单极电流发生器既可称作电流源（产生流出的电流），也可称作电流阱（产生流入的电流）。这里单极的意思是其能够产生只有一个流向的电流，通常是流向接地端。很多这样的发生器利用了晶体管的电流 - 电压特性。电压控制的电流源或阱可包括运算放大器（图 16 ）。在这样的电路中，精密和稳定的电阻 R1 确定输出电流 iout 。该电路带有通过 OPAM 的反馈环，以保持电阻 R1 的端电压恒定，因而电流也恒定。要在最大电压裕度时发送较高电流，检测电阻 R1 两端的压降需要尽可能的小。实际上所需电流等于 V1/R1 。为获得更好性能，流过输出晶体管基级的电流应该最小化，因而通常采用场效应晶体管而不是双极型晶体管作为输出电流发送器件。 众所周知，晶体管的集电极电流与集电极电压的相关性很小。这一特性被用于所谓的电流镜。电流镜具有一个电流输入和至少一个（可能有几个）电流输出。因此输出电流受输入电流控制。输入电流通过外部源（比如电压源加电阻）施加，应当具有已知的值。所谓的威尔逊电流镜具有大约与输出电流相同大小的控制电流，即具有 1 : 1 的输入 - 输出比。也可以设计出具有其它比值的镜子，比如 1 : 2 和 1 : 4 。商业化产品类的电流镜可能具有很宽的电流范围，比如美国模拟器件公司的集成电流镜产品 ADL5315 ，其电流从 3nA 到 3mA 。 图 16. 带有 OPAM 的电流源 图 17. （ a ）具有浮动负载同相电路的双极电流发生器；（ b ）具有虚拟接地的电路 对于很多传感器，可能需要双极电流发生器。这种发生器为传感器提供可以在两个反向（流入和流出）流动的激发信号。图 17 表示负载连接成反馈回路的运算放大器构成的同相（ a ）和反相（ b ）电路。通过负载 ZL 的电流等于 V1/R1 ，与负载无关。负载电流在放大器的工作范围内跟随 V1 。该电路的一个明显的缺陷是其负载是“浮动的”，即该负载没有连接到接地总线或任何其它基准电压。对于一些应用这没有任何问题，不过很多传感器需要接地或其它的参考点。示于图 17b 的电路保持负载阻抗一端接近地电位，因为 OPAM 的同相输入端是虚拟地。不过即使在这个电路中，负载依然完全与地隔离。这种隔离的一个负面影响是获取各种传输噪声的可能性增加了。 图 18. （ a ）带有负载接地参照的霍兰德电流泵的电流发生器； （ b ）具有两个 OPAM 的电流泵 在传感器必须接地的情况下，可以使用由 MIT 的霍兰德（ Brad · Howland ）发明的电流泵（图 18a ）。这种泵的工作基于对围绕运算放大器的负反馈和正反馈两者的利用。负载连接至正反馈环路。通过负载的电流由下式确定 （ 15 ） 微调电阻 P 必须调整到确保下式成立 （ 16 ） 该电路中，每个电阻或许具有相对较高的值（ 100 或更高），但 R5 的值要相对小些。这个条件改善了霍兰德电流泵的效率，因为 R5 两端消耗了较小的电压， R4 和 R3 则消耗了较小的电流。对大多数电阻负载，这个电路是稳定的，不过为了确保稳定性，可以在负反馈中或 / 和在运算放大器的正输入到地间增加几个微微法拉的电容。若负载为电感性，当施加快速瞬态控制信号时，需要无限大的跟随电压以传送设定电流。因此电流泵会产生有限的输出电流上升斜率。流动的电流会在输出端产生感应尖峰，这对运算放大器有可能是毁灭性的。对大的电感性负载，用二极管连接负载至电源总线是明智的。 一种采用四个匹配电阻和两个运算放大器的高效的电流泵如图 18b 所示。其输出电流由下式确定 。 （ 17 ） 这种电路的优点是电阻 R 可选择相对较高的值，并可封装在相同热均一性的护罩内，以便获得更好的热跟踪性能。 4.2 电压基准 电路 电压基准电路是一种产生很少受电源、温度、负载、老化和其它因素影响的恒定电压的电子器件。有几种技术常用于产生这样的电压。可获得的很多电压基准电路是单片形式，具有各种不同电压。大多数这种电路都与所谓的带隙基准电路一起工作。 4.3 振荡器 振荡器是各种电子信号的发生器。在很多利用微处理器或微控制器的应用中，可在 I/O 端口之一获得方波脉冲。若无法利用这种端口，就需要开发独立的振荡器。任何振荡器基本都由增益级和一些非线性的、带有一定数量正反馈的电路构成。根据定义，振荡器是一种非稳定电路（与放大器相对比，后者最好是稳定的！），其时间响应应该或者是稳定的，或者依据预设的函数相关性而变化。后者称为调制。通常有三种类型的电子振荡器，按计时元件分类为： RC 、 LC 和晶体振荡器。在 RC 振荡器中，工作频率由电容（ C ）和电阻（ R ）确定， LC 振荡器中则由电容（ C ）和电感（ L ）元件确定。对于晶体振荡器，工作频率由特殊切割的压电晶体（通常为石英和陶瓷）的机械谐振确定。有很多不同的振荡电路，对其作全面介绍已超出了我们的范围。下面我们简单叙述一些实用电路。 很多不同的多谐振荡器可用逻辑电路构建，例如采用 NOR 、 NAND 门或二进制反相器。并且很多多谐振荡器可由比较器或具有高开环增益的运算放大器设计构成。在所有这些振荡器中，电容和电阻的组合都是一种计时组合。这种电路被称为张弛振荡器。充电电容的端电压与另一电压相比较，该比较电压或者是恒定的，或者以不同速率变化。两者电压相等的时刻由比较器测定。比较指令反馈到 RC 回路，以相反方向改变电容的充电，即放电。以新的方向再次充电至下一个比较时刻。以这种基本原理工作起码需要如下最少组件：一个电容，一个充电电路，一个阈值器件（比较器）。一些单片张弛振荡器可由很多制造商处获得，例如非常普及的计数器 555 型，这种电路能够工作在单稳态或非稳态模式。作为例证，下面我们仅叙述两种分立元件方波振荡器，不过这类电路多种多样，读者可参考关于运算放大器和数字系统的相关书籍。 一种非常普及的方波振荡器（图 19 ）可由 OPAM 或电压比较器构建。放大器带有两个反馈环路：一个是负的（连接至反相输入），另一个是正的（连接至同相输入）。正反馈（经由 R3 ）控制阈值电平，而负反馈环路则通过电阻 R4 使定时电容 C1 充电和放电。该振荡器的频率可由下式确定 ， （ 18 ） 其中 是电阻 R1 和 R2 并联时的等效电阻。 图 19. 采用 OPAM 的方波振荡器 图 20. LC 正弦波振荡器 图 20 中所示的两种电路能够产生正弦波信号。该电路采用 npn 晶体管作为放大器， LC 回路用于设定振荡频率。电路（ b ）在驱动 LVDT 位置传感器时特别有用，因为传感器的变压器成为了振荡电路的一部分。 图 21. 作为电容式占位探测器的 LC 射频振荡器 射频振荡器可用于电容式占位探测器的一部分，在其天线附近探测人的存在（图 21 ）。天线是个线圈，与电容 C2 共同确定振荡频率。天线通过其分布式电容与环境耦合，使振荡器的频率有所减小。当有人进入天线附近时，引入了额外的电容，进一步降低了振荡器频率。振荡器的输出与谐振回路（典型情况是 LC 回路）耦合，该回路调谐在基准频率（接近 30MHz ）。 4.4. 驱动器 与电流发生器相反，电压驱动器必须在宽的负载范围上产生输出电压，且工作频率与输出电流无关。有时电压驱动器称为 硬电压源 。当要驱动的传感器是纯电阻时，通常驱动器可以是简单的输出级，能够提供足够的电流。不过当负载包括电容或电感，即负载为电抗性的，输出级就成为一个相当复杂的装置。 在很多实例中，虽然负载是纯电阻，还是会有一些电容性与之相关。这可能发生在负载连接于很长的电线或同轴电缆的情况。如果同轴电缆的长度大于同轴电缆中所需频率对应的波长的 1/4 ，同轴电缆就表现为连接在其中心导线和屏蔽层之间的电容。同轴电缆的最大长度由下式给出 ， （ 19 ） 其中 c 是同轴电缆介质中的光速。 举例来说，如果 f=100kHz ， =49.5 ，即电缆大于 49.5 m 时将表现为并联于负载的电容（图 22a ）。对规格为 RG-58A/U 的电缆，其电容为 95pF/m 。出于两个理由必须考虑这个电容：电路的工作速率和稳定性。不稳定起因于由驱动器输出电阻 RO 和负载电容 CL 产生的相移： 。 （ 20 ） 例如，如果 R=100 ， C=1000pF ，在 f=1MHz 时，相移 。这个偏移明显减小了反馈回路中的相位裕度，这会导致响应的显著变差，降低驱动电容性负载的能力。当整个系统振荡时，不稳定就成为整体性的；或者当驱动器自身失稳时，不稳定性则是局部的。局部不稳定性可用连接于电源两端的大旁路电容（ 10 量级）解决，或者用所谓的 Q 抑制器，由串联的 3 ～ 10 电阻和盘式陶瓷电容连接驱动器电源端至接地构成。 图 22. 驱动电容性负载。（ a ）负载电容通过反馈与驱动器输入耦合；（ b ）电容负载的解耦 要使驱动级对电容性负载更加兼容，可以用小的串联电阻进行隔离，如图 22b 所示。小的电容（ Cf ）反馈至放大器的反相输入端， 10 的电阻则能够驱动大到 0.5 的负载。不过在任何具体情况下，推荐采用实验方法找出该电阻和电容的最佳值。 4.5 光学驱动器 在一些应用中，光学传感器接收来自自然光源的光，例如天体或火焰，也接收来自人造光源的光，例如闪光材料、白炽灯或荧光灯。在很多其它情况下，必须提供特殊光源。一个例子是电视机遥控接收器的光探测器。这种传感器在接收到来自遥控发送器的连续光（近红外）脉冲时才会产生输出。发送器必须包含具有匹配光谱特性的光发射器。最常见的光发射器是发光二极管（ LED ），其工作在从 UV 至近红外频谱范围。 LED 产生的光的强度近似正比于流过二极管的电流。用于 LED 的最简单的驱动电路示于图 23a 。该电路包括一个 dc 电压源或是脉冲电压源，以及一个限流电阻 R 。电流 i 由下式确定 ， （ 21 ） 其中 VD 是 LED 两端的电压（典型情况为 1.5 至 2.0V ）。此电压与电流和温度有关，因而由 LED 产生的光的强度也与电流和温度有关。对于精确的应用，流过 LED 的电流应该维持恒定。因此取代限流电阻的，是采用电流源，如图 23b 所示。此驱动器中，电流只由驱动控制电压和测量电阻 R 确定，因而与温度无关。 图 23. 用于 LED 驱动器的电阻（ a ）和电流源（ b ）