格雷码: 任意两个相邻的代码之间, 只有一位二进制数不同的BCD码. 常用在大于24个状态的状态机设计中.
一. 自然二进制码转换为二进制格雷码
原理: 若二进制码表示为: B[N-1]B[N-2]...B[2]B[1]B[0];
相应地, 则二进制格雷码表示为: G[N-1]G[N-2]...G[2]G[1]G[0].
其中最高位保留: G[N-1] = B[N-1];
其他各位: G = B[i+1] xor B. (i = 0, 1, 2, ..., n-2)
Binary_to_Gray.v / Verilog
module Binary_to_Gray (
input [N-1:0] B,
output reg [N-1:0] G
);
parameter N = N_bit_Binary; // 设置自然二进制码的位宽
input [N-1:0] B,
output reg [N-1:0] G
);
parameter N = N_bit_Binary; // 设置自然二进制码的位宽
integer i;
always @ (B)
begin
G[N-1] = B[N-1];
for (i=0; i<N-1; i="i"+1)
G = B[i+1] ^ B;
end
begin
G[N-1] = B[N-1];
for (i=0; i<N-1; i="i"+1)
G = B[i+1] ^ B;
end
endmodule
仿真波形
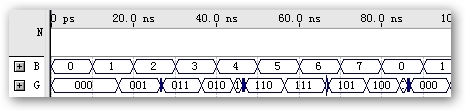
图1. N="3"
图2. N="4"
二. 二进制格雷码转换为自然二进制码
原理: 若二进制格雷码表示为: G[N-1]G[N-2]...G[2]G[1]G[0];
相应地, 则二进制码表示为: B[N-1]B[N-2]...B[2]B[1]B[0].
其中最高位保留: B[N-1] = G[N-1];
其他各位: B[i-1] = G[i-1] xor B. (i = 1, 2, ..., n-1)
Gray_to_Binary.v / Verilog
module Gray_to_Binary (
input [N-1:0] G,
output reg [N-1:0] B
);
input [N-1:0] G,
output reg [N-1:0] B
);
parameter N = B_bit_Gray; // 设置二进制格雷码的位宽
integer i;
always @ (G)
begin
B[N-1] = G[N-1];
for (i=1; i<=N-1; i="i"+1)
B[i-1] = G[i-1] ^ B;
end
endmodule
begin
B[N-1] = G[N-1];
for (i=1; i<=N-1; i="i"+1)
B[i-1] = G[i-1] ^ B;
end
endmodule
仿真波形
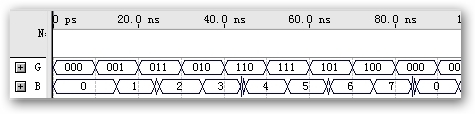
图3. N="3"
图4. N="4"
三. 故障分析
在转换时, 出现很多毛刺, 不知怎样消除. 希望有高人指点.
四. 其他
本文可作为Verilog的for循环的学习实例.
五. 参考资料
1. 游志宇, 二进制格雷码与自然二进制码的互换;
2. Pandeng, FSM 设计指导.
- 上一篇： N倍偶数分频器.(Verilog)
- 下一篇： 使用函数传回整数的百十个位.(C)
文章评论（1条评论）
登录后参与讨论
相关推荐阅读
-
用户1373959 2009-11-17 22:44
- 本博客地址迁移.(公告)
- 迁移至：http://yuphone.cnblogs.com/...
-
- 七段数码管动态显示IP的研究及设计.(Nios II)(SOPC Builder)
- 这两个礼拜整理的，欢迎大家抓虫。...
-
- sizeof()和strlen()的区别.(C)
- #include <stdio.h>int main(void){ char msg[] = "Hello Nios!"; printf("sizeof(msg) = %ld", ...
-
- HAL的不同方式访问字符器件的空间开销简单比较.(Nios II)
- Unix类型 #include "system.h"#include "fcntl.h"#include "unistd.h"int main(void){ int fd; // file desc...
-
- 几个的Ubuntu 9.04好源.(Ubuntu)
- 新加坡国立大学理学院 - 全国通用deb http://ftp.science.nus.edu.sg/ubuntu/ jaunty main restricted universe multivers...
-
- NI Multisim 基础电路范例.(Multisim)
- NI官网提供的NI Multisim Fundamental Circuits, 内容涵盖RLC电路, 二极管, 晶体管, 放大器, 运放, 滤波器和混合电路. 这些内容不仅可作为初学者的学习范例, ...
EE直播间
更多
-
提升毫米波信号测试精度 直播时间： 12月18日 14:00 -
EE Talk主题专访系列直播-对话：释放 Wi-Fi 7 在高带宽应用中的技术潜力 直播时间： 12月19日 10:00
关闭
站长推荐
/2 
/2
-
返回顶部
-
用户1455274 2009-8-7 13:53