


随着FPGA的发展,其中包含的DSP资源原来越丰富,并且伴随着其结构的优化,在FPGA中实现各种复杂的数字信号处理算法显得游刃有余,很多系统设计从之前的CPU+DSP+FPGA架构慢慢地向单片FPGA转变,并且已经有了实际应用,如Xilinx的Zynq、Altera的Soc FPGA。趁着这次【博客大赛】,决定系统全面地整理、学习一下FPGA中的DSP,从这篇博文开始这个【DSP in FPGA】专题。
专题一:数字表示
自从计算机发明以来,数学运算进入了二进制的世界,简单的0、1变化能组成几乎所有的运算:加法、减法、乘法、除法,甚至三角函数、对数、开方等。对于电子工程师而言,数字电路占据了一半江山,由数字门电路组成的FPGA应该属于二进制世界范畴。
在FPGA中的数字表示基本分为两类:定点数和浮点数,其实不止FPGA,其它算术处理器也是按照此分类。定点数处理具有速度快和成本低的特点,而浮点数处理其动态范围高并且运算无需转换,在FPGA设计前期,需要确定采用定点数还是浮点数实现。
1. 定点数
FPGA设计中常用的定点数有无符号整数、有符号整数和二进制补码。
有N位二进制数xN-1xN-2…x0
无符号整数(unsigned):xN-1是最高有效位MSB,x0是最低有效位LSB,其取值范围是[0,2N-1]
有符号整数(signed):xN-1是符号位,其它N-1位代表数值,其取值范围是[-(2N-1-1),(2N-1-1)]
二进制补码(two’s complement):其取值范围是[-2N-1,2N-1-1],二进制补码表示法是数字信号处理领域最为流行的有符号数字表示法;它累加多个有符号数时,中间过程如果出现溢出但是最终结果是在有效范围之内,溢出可以忽略,如3位有符号数运算3+2-3=2,3+2=(011+010)2=1012,101用二进制补码表示为-3,溢出了,但是(101-011)2=(101+101)2=0102=210,结果是正确的。在FPGA中的有符号型数默认由二进制补码表示。
如下表所示以3位二进制数为例,编码的到的三种定点数的表示
|
|
无符号整数 |
有符号整数 |
二进制补码 |
|
000 |
0 |
0 |
0 |
|
001 |
1 |
1 |
1 |
|
010 |
2 |
2 |
2 |
|
011 |
3 |
3 |
3 |
|
100 |
4 |
-0 |
-4 |
|
101 |
5 |
-1 |
-3 |
|
110 |
6 |
-2 |
-2 |
|
111 |
7 |
-3 |
-1 |
HDL语言中的定点数表示也很多样,以下分别按Verilog HDL和VHDL作说明:
Verilog HDL:在Verilog-2001中,申明reg和wire时,可加入signed、unsigned关键字申明reg和wire是有符号型还是无符号型,如reg signed [7:0] cnt表示申明一个8位有符号型reg,不加申明默认为unsigned。并且在HDL程序中变量可以在有符号型和无符号型间转换,$signed(x)表示将变量x转换为有符号型表示,$unsigned(x)则表示将变量x转换为无符号型表示,其中转换过程并不会导致变量中具体位0、1间变化,只是表示方式的变化,在参与运算时结果将会发生变化。
VHDL:在VHDL中没有申明变量是有符号数或者无符号数的关键字,只有在开头加入库文件中指定运算操作为有符号型还是无符号型:ieee.std_logic_unsigned.all和ieee.std_logic_signed.all,分别对应std_logic_signed.vhd文件和std_logic_unsigned.vhd文件,如图1所示为两个文件的部分对比,其中左边部分为signed,右边部分为unsigned。红色部分为两文件差别,从第一个红色处,可以很清楚的看到std_logic_signed库定义的加法首先将变量转化为有符号型,而std_logic_unsigned库定义的加法首先将变量转化为无符号型。其中VHDL中也定义了有符号型、无符号型间转换的函数:CONV_SIGNED(x)和CONV_UNSIGNED(x)
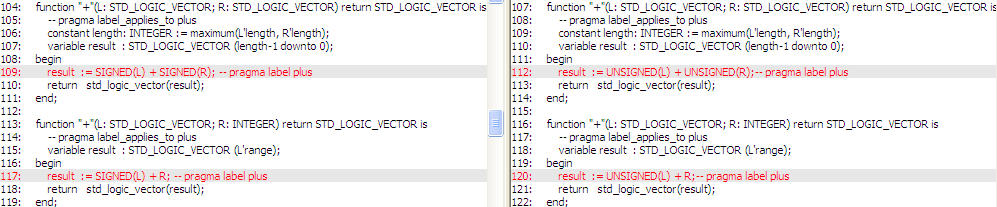
图1
为了说明有符号型数和无符号型数的运算区别,编写了一个累加器的小程序(Verilog),如下:
module test_2c(
input clk,
input rst,
input [2:0] a,
output reg [2:0] sum_unsigned,
output reg signed [2:0] sum_signed
);
always@(posedge clk)
if(rst)
begin
sum_unsigned<=3'd0;
sum_signed<=3'd0;
end
else
begin
sum_unsigned<=sum_unsigned + a;
sum_signed<=sum_signed + $signed(a);
end
endmodule
其中sum_unsigned和sum_signed分别为无符号数和有符号数的累加值,并且不考虑溢出情况,如图2所示为仿真图,实现了(011+011+100)2的运算,用无符号型表示的sum_unsigned因(110+100)2发生了溢出,最终结果是错误的;而用有符号型表示的sum_signed虽然中间过程(011+011)2发生溢出,但是因二进制补码的特性,此溢出可以忽略,最终得到正确的结果。

图2
另外在定点数运算中,比如两个数累加或相乘之后都需要位扩展,对于中间过程这种位扩展是为了精度需要,但是作为结果输出时往往需要对扩展位进行截断(truncate)或者舍入(round)处理,截断则是直接丢掉扩展位,不做任何舍入处理;舍入则是为了减小误差加入的四舍五入操作:定义舍入之前全精度数为M位,舍入后的数为N位,其中N,当全精度数为无符号数或者数为正的有符号数时,如果舍入相邻位(多余位数中的最高位)中最高位为1,则舍入时必须进1,反之不进位;当全精度数为负的有符号数时,舍入相邻位为1且舍入相邻位后面还有一位为1,则舍入时需进1,反之不进位。分别用verilog>
//Verilog
wire [3:0] dout;
wire [7:0] din;
wire c;
assign c=(din[7]==1’b1) ? ( din[3] & (|din[2:0]) ) : din[3];
assign dout=din[7:4] + {3’b000,c};
--VHDL
signal dout:std_logic_vector(3 downto 0);
signal din:std_logic_vector(7 downto 0);
signal c:std_logic;
begin
c<= din(3) and (din(2) or din(1) or din(0)) when din(7)=’1’ else din(3);
dout=din(7 downto 4) + (“000” & c);
end
2. 浮点数
浮点数具有比定点数更高的精度和更大的动态范围,标准的浮点数由一个符号位s(sign)、指数e(exponent)和无符号的规格化尾数f(fraction)构成,格式如下:
|
符号位s |
指数e |
尾数f |
表达式如下:
其中bias=2E-1-1,E位指数的位数。
举一个例子说明定点数和浮点数之间的转换吧!
定点数—>浮点数:十进制数16.5用12位(1,6,5)浮点数格式表示:
16.510=(10000.1)2=(-1)0×1.00001×24,
可以得到s=0,bias=26-1-1=31,e=4+bias=3510=1000112,f=00001,因此16.75的12位浮点数表示为0 100011 00001
如果用上述的12位(1,6,5)浮点数格式表示数,绝对值最大可取到±1.11111×231≈±4.228×109——决定了取值范围,绝对值最小可取到±1.00000×2-30≈±9.31×10-10——决定了精度;而12位定点数如二进制补码的取值范围为[-2048,2047],因此同样位数浮点数的动态范围和精度都远远优于定点数。
IEEE754-1985中定义了两种浮点数标准:单精度标准和双精度标准。具体的定义如下:
|
|
单精度 |
双精度 |
|
字长 |
32 |
64 |
|
尾数 |
23 |
52 |
|
指数 |
8 |
11 |
|
偏移 |
127 |
1023 |
|
范围 |
2128≈3.8×1038 |
21024≈1.8×10308 |
在IEEE754-1985标准中,舍入处理提供了四种可选方法:
就近舍入:其实质就是四舍五入,例如尾数超出规定的23位的多余位数字是10010,多余位的值超过规定的最低有效位值的一半,故最低有效位应增 1。若多余的5位是01111,则简单的截尾即可。对多余的5位10000这种特殊情况:若最低有效位现为0,则截尾;若最低有效位现为1;则向上进 一位使其变为 0。
朝0舍入:即朝数轴原点方向舍入,就是简单的截尾。无论尾数是正数还是负数,截尾都使取值的绝对值比原值的绝对值小。这种方法容易导致误差积累。
朝+∞舍入:对正数来说,只要多余位不全为0则向最低有效位进1;对负数来说则是简单的截尾。
朝-∞舍入:处理方法正好与 朝+∞舍入情况相反。对正数来说,只要多余位不全为0则简单截尾;对负数来说,向最低有效位进1。
在FPGA实现中,通常不严格采用IEEE754-1985标准的浮点数,而是根据实际动态范围和精度的需要来选择浮点数格式。关于浮点数的运算在【DSP in FPGA】专题后续章节中会详细介绍。
 /2
/2 
文章评论(0条评论)
登录后参与讨论