原创 【博客大赛】直接型FIR的FPGA设计（二）

 （二）FIR算法的定点仿真

从（一）上设计可得知，滤波器阶数为241阶，系数个数242，并且具有线性相位，系数具有偶对称结构。

首先滤波器进行浮点仿真 来作为我们定点仿真的验证参考。

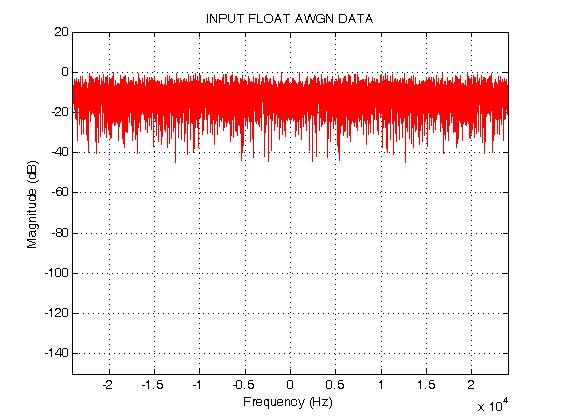
生成激励信号：选用高斯白噪声作为激励信号，生成采样率为48kHz，共100*242点激励信号，其功率谱如：

FIR时域计算公式可展开得到：

y(n) = h(0)x(n) + h(1)x(n-1) + h(2)x(n-2) + …… + h(N-1)x(n-N+1)

FIR运算即为一种卷积运算，所得结果=输入数据与FIR系数的卷积。其定点仿真则可通过下面简单的程序完成：

% float simulate
% AWGN
output_float = conv(input_float , coef_float);
output_float = output_float(1:simdata_len);

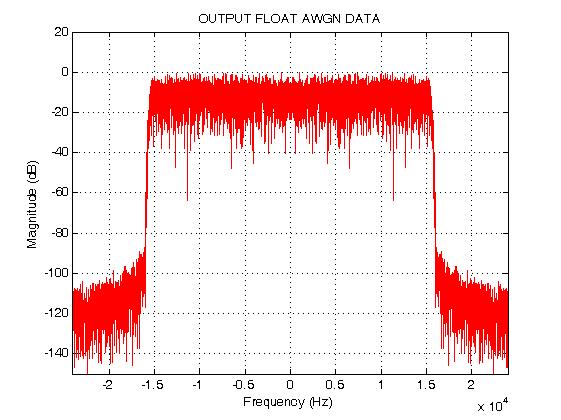
所得结果的功率谱：

而我们采用的定点算法，即是将卷积运算用相乘与累加运算来代替实现，并通过控制将其更便于在FPGA硬件电路上实现，matlab程序如下：

% fixed simulate
%AWGN
output_fixed = zeros(simdata_len-coef_len+1,1);
for i = 1 : simdata_len-coef_len
    sum_data = 0;
    data_ram = input_fixed(i : i + coef_len - 1);
    for j = 1 : coef_len
        sum_data = data_ram(j)*coef_fixed(j) + sum_data;
    end
    output_fixed(i) = floor(sum_data/2^(in_word_len+coef_word_len-out_word_len-1));
end

所得结果功率谱与浮点的结果进行比对：

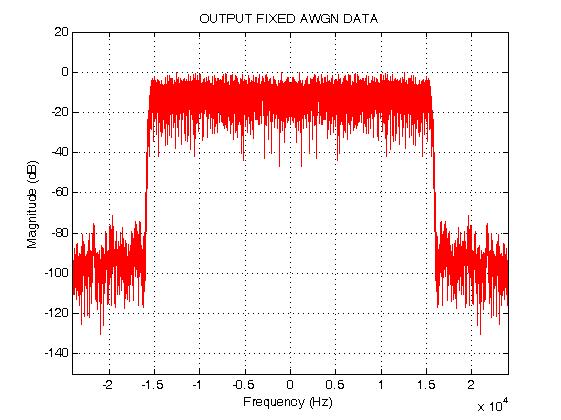
可知，我们所采用的移位相乘累加的方法可以直接实现FIR滤波器的运算。随后我们将在FPGA上用这种直接型结构来实现FIR滤波器。