


Barry Xiao--- China Telecom Application Team
摘要
AMC1204 是一款二阶隔离Delta-Sigma 调制器,由于其出色的直流特性、交流特性及隔离特性,广泛应用在通信电源系统、逆变器、整流器、UPS 及电机控制中,可实现系统电源电压及电流的检测和监控。本文简单介绍了AMC1204 的工作原理,重点讨论输入采样电阻阻抗对AMC1204 转换精度的影响以及调制器输出滤波器的设计。
AMC1204 是一款二阶隔离Delta-Sigma 调制器。如图1 所示,它使用TI 特有的电容隔离技术,满足UL1577,IEC60747-5-2 及CSA 认证标准,隔离工作电压可达1200Vpeak,瞬间隔离电压达4000Vpeak,共模瞬态抑制在15KV/us 以上。电容隔离器件具有同电感隔离器件相比更高的磁场抗扰性及可靠性,同光耦隔离器件相比更低的功耗等这些显著的优点,同时AMC1204 内部集成了高精度的Delta-Sigma 调制器,电路设计简单,被广泛应用于通信电源系统、逆变器、整流器、UPS 及电机控制等场景。
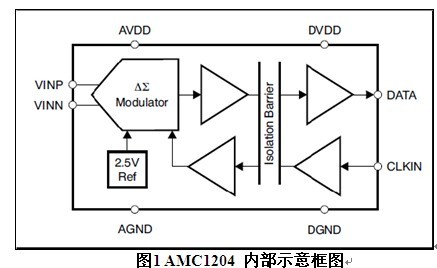
AMC1204 具有出色的直流特性,DNL 误差小于1LSB,INL 误差最大为8LSB(-40℃至85℃),失调误差1mV,增益误差小于2%。如果将失调和增益误差校正后,不考虑电源及温度的影响,由ADC 引入的误差仅为0.012%。此外,AMC1204 也表现出了不错的交流特性, SNR 可达88dB,THD 可达-96dB,有效位数ENOB 可达14bit(OSR=256,
滤波器)。因此,AMC1204 可以满足绝大多数高精度系统的使用要求。图2 是在通信系统电源中的一个检测电压和电流的典型应用电路,该电路使用两片AMC1204 实现对48V 电源的电压监测及负载电流检测,输出数字信号给后端进行处理,不需要额外使用隔离器件,应用电路设计更简单、更可靠。
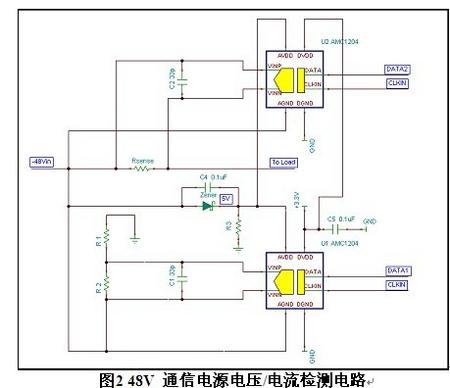
在电路设计中,影响AMC1204 转换精度主要是外围电路的电阻取值,尤其在通过电阻分压电路测试电压值的应用场景中。下面分析输入采样电阻对AMC1204 转换精度的影响。
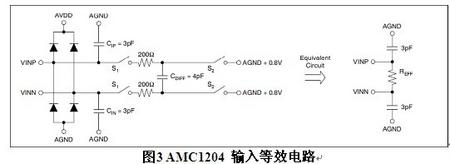
AMC1204 的输入等效电路如图3 所示,在一个时钟周期内,完成一次采样/放电,输入等效电阻
。当AMC1204 的输入时钟频率为5MHz 时,等效阻抗约为50KΩ;当输入时钟频率为20MHz 时,等效阻抗约为12.5KΩ。如果待测信号的阻抗较大,则输入等效阻抗的影响不能忽略,因为这将可能严重影响到ADC 转换的精度。因此,实际使用时,需要根据系统的性能要求,选择满足测量精度的采样电阻值。
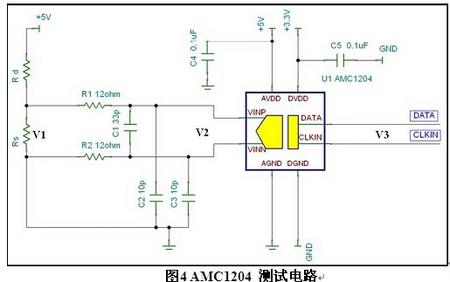
以图4 所示电路为例, 如果不考虑器件输入等效电阻的影响, 输入差分电压理论值为
。考虑到输入等效电阻, 实际输入差分电压应为
。
以
为例,则当
时,由输入等效电阻
引入的误差约为0.96%;当
时,由输入等效电阻
引入的误差约为0.1%。因此,实际应用时,如果要系统精度达到1%以上,则需要采样电阻的阻抗小于0.01
,以尽量减小由输入采样电阻引入的误差。
使用图4 所示电路测量不同输入采样电阻和时钟频率情况下AMC1204 转换精度。实验使用
作为调制器后端的硬件滤波器,滤波器配置为
型,过采样率(OSR)设置为256。实验结果如表1 所示。
是输入电压的目标值,
是VINP 管脚与VINN 管脚之间电压实测值,
’ 是VINP 管脚与VINN 管脚之间电压理论计算值(考虑到输入阻抗的影响),
是由调制器的输出经滤波器后的转换结果。
注:实验所选电阻精度为1%,实际测量值由Agilent U1251A 型号万用表测得,AMC1204 的失调误差和增益误差未校正(以上测试结果供参考)。
表1 不同输入采样电阻和时钟频率下的转换结果
以上实验结果可以看出,实测的输入电压值
与考虑到输入阻抗计算得到的理论值
基本一致,实验得到的数据与理论分析基本吻合。输入时钟频率直接决定了AMC1204 的输入阻抗,输入采样电阻值相对于AMC1204 的输入阻抗越低,输入采样电阻的影响就会越小。因此,在一些测量电压的应用场景下,如果采样电阻值无法减小,可以使AMC1204 工作在较低的时钟频率以提高输入阻抗,获得较高的转换精度。当然,降低输入时钟频率是以牺牲转换速率为代价的。此外,如果无法通过降低输入时钟频率和输入采样电阻的方式提高精度,还可以通过软件方法对AMC1204 的失调误差和增益误差进行校正,即对表1 中的误差指标进行额外补偿,以提高系统精度,获得最佳的系统性能。
AMC1204 输出1 比特位宽由0 和1 组成的数据流,数据流中1 的密度与模拟输入电压成正比。当输入电压为250mV 时,输出1 的比例为89.0625%;当输入电压为-250mV 时,输出1 的比例为10.9375%;当输入电压为0mV 时,输出1 的比例为50%。当输入电压从-250mV 到+250mV 之间,AMC1204 的转换性能可以得到保障。为了得到真实的输出数据信息,一般需要在输出后端进行数字滤波处理,实际应用中可以采用以下两种滤波器对输出数据进行处理。
移动平均滤波器比较简单,它是取输入信号的最近的一些值,进行算术平均,相当于一个低通滤波器,滤除高频分量,保留低频分量。在时钟clk 的上升沿,对AMC1204 输出的高脉冲进行计数,计算M 个clk 的上升沿时,对应的高电平脉冲个数N。则,对应的转换结果为(640*N/M-320)mV。平均的项数越多,即M 越大,则得到变化越缓慢的输出信号,但得到的精度也越高。
需要注意的是,在实际应用中,这种方法必须平均尽可能多的输入信号才能获得比较高的精度。移动平均滤波器实现比较简单,不需要单独增加DSP 或FPGA 即可实现。但是,移动平均滤波器的频域效果较差,滚降较慢,因此,在检测低频信号及对精度要求不高的应用中,可以考虑使用这种方法。但是,对于精度要求比较高的应用中,需要考虑使用性能更好的滤波器,如Sinc 滤波器。
Sinc滤波器具有良好的频域特性,较低的成本和功耗,延时较低,因此,广泛用作Delta-Sigma DAC 的滤波器。Sinc 滤波器可通过专门的滤波器芯片或者通过FPGA 或DSP 算法来实现。
AMC1210 是一个4 通道的数字滤波器,芯片输出接口可设置为SPI 接口或者并行接口方式,方便与CPU 进行数据通信。数字滤波器可设置为Sincfast,
,
或者
方式。实际应用时,由于
滤波器具有更好的低通特性,建议将AMC1210 配置为
滤波器,过采样率(OSR)设为256以获得最优的转换结果。
此外,也可以通过FPGA 或DSP 来实现Sinc 滤波器算法。滤波器的基本架构如图7 所示。
以下是用VHDL 语言实现SINC3 滤波器的一段示例程序。其中,CNR=MCLK/M,M 为抽取率(即过采样率OSR)。
图8 的示例代码:
library IEEE;
use IEEE.std_logic_1164.all;
use IEEE.std_logic_unsigned.all;
entity FLT is
port(RESN, MOUT, MCLK, CNR : in std_logic;
CN5 : out std_logic_vector(23 downto 0));
end FLT;
architecture RTL of FLT is
signal Z1 : std_logic_vector(23 downto 0);
signal Z2 : std_logic_vector(23 downto 0);
signal Z3 : std_logic_vector(23 downto 0);
signal Z4 : std_logic_vector(23 downto 0);
signal Z5 : std_logic_vector(23 downto 0);
signal Z6 : std_logic_vector(23 downto 0);
signal Z7 : std_logic_vector(23 downto 0);
begin
process(MCLK, RESN)
begin
if RESN = '0' then
Z1 <= (others => '0');
Z2 <= (others => '0');
Z3 <= (others => '0');
elsif MCLK'event and MCLK = '1' then
Z1 <= Z1 + MOUT;
Z2 <= Z2 + Z1;
Z3 <= Z3 + Z2;
end if;
end process;
process(CNR, RESN)
begin
if RESN = '0' then
Z4 <= (others => '0');
Z5 <= (others => '0');
Z6 <= (others => '0');
Z7 <= (others => '0');
elsif CNR'event and CNR = '1' then
Z4 <= Z3;
Z5 <= Z3 - Z4;
Z6 <= Z3 - Z4 - Z5;
Z7 <= Z3 - Z4 - Z5 - Z6;
end if;
end process;
CN5 <= Z7;
end RTL;
应用高性能隔离Delta-Sigma调制器AMC1204时,为了确保转换精度,需要注意外围输入电路的设计,选择合适的输入采样电阻以及时钟频率,使得输入采样电阻阻值相对于输入等效阻抗尽量小,以此降低输入电阻引起的转换误差;同时选择合适的输出滤波器,以满足整个系统对测量精度的要求。
[1] AMC1204 datasheet
[2] AMC1210 datasheet
 /2
/2 
文章评论(0条评论)
登录后参与讨论