原创 The tricky gravitational constant G

While all these constants are important, some of them are far removed from our daily lives. But one is not: the gravitational constant G. Even since Isaac Newton formulated the law of gravitational attraction F = G (mass1 × mass2)/r2, inspired by that apple falling from a tree, the value of G has been of great interest. Given how pervasive and accessible gravity is, it should be pretty easy to measure G accurately, right?

Well, yes and no. It turns out that gravity is easy to measure, but hard to measure with precision. A fascinating article in the latest issue of Physics Today, "The search for Newton’s constant," discusses the history of measuring G. It looks at the various experimental setups that have been used over several hundred years (torsion-balance, pendulum, beam-balance, and others) and the data spread in results of each. Some of the sophisticated tests by serious researchers produce results with low uncertainty, yet they differ significantly from other tests, which also claim low uncertainty.

While researchers have certainly improved the accuracy and precision of their results, the article explains why G is still so hard to measure. It's not only an interesting, well written article, it's also a sobering and thought-provoking one as well, because you likely assumed that G's value is pretty much nailed down solid, end of story.

Yet, as most engineers and scientists know, getting consistent, accurate results in any test-and-measurement challenge to better than three or four significant figures is rarely easy. Every added significant figure means ever-more-subtle sources of error must be uncovered, understood, calibrated out, or compensated for in the fixture and equipment.

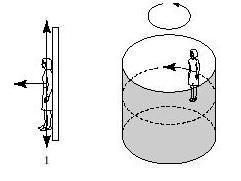
If you're lucky, the test can be structured so some of these errors actually drop out, or self-cancel, much as the value of mass m cancels out in some basic physics experiments and even carnival rides, such as the "rotor ride" or Gravitron (Figure 1) where participants "stick" to the wall via centripetal force and friction. The mass of the person doesn't matter, only the size of the rotor, the speed of rotation, and the coefficient of friction between their clothes and the wall (Figure 2). (If you can't explain why the person sticks, and why their weight is not a factor, go to a basics physics book.)

Figure 1

The Gravitron's rotor spins and pins people to the wall. A functionally similar but more sophisticated version is used in centrifuges to acclimate astronauts to high-G environments. (Source: NASA)

 

Or maybe there's another explanation about the elusiveness of a precise, accurate value of G, one that keeps physicists and metrologists worrying: Perhaps the "squared" exponent in the denominator of Newton's Law is not exactly 2.0 out to as many places as you care to pick. Or maybe G itself is not a true constant, but actually changes slightly over time and place. Stranger things have happened; just ask those physicists who believed in the absoluteness of time and distance, but had to change their beliefs to accommodate the curvature of time and space, as well as time dilation itself and even E = mc², as Einstein's 1905 paper on Special Relativity became accepted principle.

Figure 2

The rotor ride spins and people inside the cylinder stick to the wall, irrespective of their mass. Riders are subject to three forces: weight, normal force, and frictional force.
(Source: stuegli.com)

 

Have you ever had a constant or fixed assumption in engineering or science that you had to abandon or at least become flexible about? Have you ever stopped and wondered what "gravity" is, as well? What are your thoughts are gravity waves and gravitational frame-dragging, as Gravity Probe B is exploring?