原创 第五章 端接

1.        端接

根据传输线上负载端信号的求和公式，如果阻抗与传输线的阻抗不匹配，将发生发射，干扰信号的接受，因此，对于不匹配的传输线，需要端接。

如果线路很短的话，相当于H(w)=1，那么S=A(w)T(w)/(1-R1(w)R2(w))=ZL/Zs+ZL，得到的结果是只有Zs和ZL，而没有传输线的阻抗，也就是说，这种情况下，信号的波形是由驱动器和负载的阻抗决定的，而和线路没有关系，即使在线路没有匹配的情况下。H(w)=1的条件是，线路的长度小于信号上升沿的1/6。这似乎意味着，对于一段短的传输线，我们不需要端接。但是，这种规则的应用有一个重要的隐含假设，即，驱动器的驱动阻抗不能比线路阻抗小太多。如果不满足这个假设条件，某些负载条件下，短线可以引起振铃。

1.1    短传输线的谐振[19]

当一条传输线成为短线的时候，可以近似为一个集总的参数模型。但是，集总参数的电路可能振铃，也可能不振铃，这取决于电路的Q值。Q值在技术上定义为总存储能量和每周期衰耗的能量之比。显然,Q值高的电路，信号衰减的慢，Q值低的电路，信号衰减的快。如果信号衰减的很慢，即Q很高，那么信号就会在多个周期内来回的振荡，经过几个振铃周期才慢慢的消失。因此，如果集中参数电路的Q值过大，也会产生振铃现象。[1]的第四章开始，有一个很好的例子探讨这个问题。

        一个经验值是:Q值为1的电路显示出16%的过冲，Q值为2的电路显示出44%的过冲，任何Q值低于1/2的电路都不会过冲或振铃。可以用下边的公式估算电路的Q值[1] pp-96。这个公式可以理解为：传输线存储的能量和消耗在源端电阻Rs上的能量的比值。

对于一段短传输线，可以用pi模型来表示。系统的模型是：Driver--RS ---(50 ohms, 176 ps/in.)----(CL to ground)

考虑下面这样一个传输线的结构：

A short transmission line with a capacitive load sometimes rings horribly.

    这个电路中，信号上升时间1ns，传输时延176ps，驱动器的输出电阻10ohm，传输线的长度大约为上升沿电气长度的1/6，这是短线！！！负载电容CL 。varies from 0-200 pF。

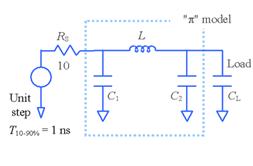
当线路长度小于上升沿电气长度的1/6时，pi模型的精度大约是2%，这是在负载条件为普通负载的前提下，也就是是数字电路中通常的负载。当线路长度是上升沿电气长度的1/3时，精度劣化到20%.因此，使用这个模型的时候，精度很重要。

传输线的特性阻抗是Z0，时延t_d，电感L= L = t_d*Z₀ ；电容C₁ = C₂ = (1/2)(t_d/Z₀)。传输线总的有效电容是t_d/Z₀ ，这两个电容是并联。

在没有负载的情况下，这条传输线和Rs串联的阻抗为:

Z=Rs+Zc1//(ZL+Zc2)=Rs+(1/jwc1)//(jwL+1/jwc2)

谐振频率是：

f=2/2*pi*sqrt(LC1)=1/pi*sqrt(LC/2)=1/4.4*sqrt(LC)

=1/4.4*Td

如果满足假设条件，即td=Tr/6，那么，

f_r = (1/4)(1/t_d) = (1/4)(6/t_r) = (3/2)(1/t_r) [3].<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />

这说明了，谐振频率是转折频率fknee = (1/2)(1/tr)的3倍。根据第1章的知识，一个数字电路的能量主要集中在fknee 以下，fknee 以上的频率特性对它如果处理数字信号几乎没有影响！这就是为什么在短线的情况下，我们不需要端接的更深层次的原因，而这个经验法则也一直被我们应用着。

注意，这个公式的一个前提条件是unloaded line！！

如果增加负载，谐振频率就要降低；另外，我们注意到Q的公式中的Rs项，它指出了这个电路振铃的可能。因此，当传输线带载时，谐振频率要向fknee移动，同时较低的Rs会产生较高的Q值，因此，在某个CL的情况下，电路会发生振铃，即短传输线也可能振铃。下面给出这个电路的仿真结果。

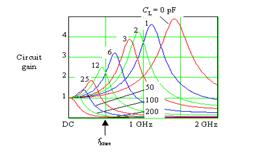
负载从0pf开始，随着负载的增加，电路的谐振频率降低。大于12pf的负载，谐振频率都低于电路的转折频率——f_knee。

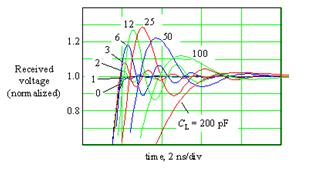
振荡的越厉害，说明Q值越高，如果想减小振铃，就要减小Q值。根据fig3，4，我们可以看出，想减小这个电路的振铃和过冲，有下面这些办法：

（1）减小CL，让谐振频率越过转折频率。To make this work you need CL << C1 = (1/2)(td/Z0) [4]这个公式很明显，让CL尽量小的可以忽略的地步

 (2)增加CL，减小Q值。我们希望Q<1，这样，电路显示出16%的过冲。因为Q<1所以Q^2 <1。Increase the load capacitance to the point where the line reacts in a critically-damped fashion. This approach sacrifices speed for monotonicity, a good trade in some cases (especially for relatively slow clocks produced by overly speedy drivers). To make this work you need(CL + 2*C1) > (L/(RS*RS)) = (tdZ0/(RS*RS))[5]。

（3） 也可以增大Rs。From the critical-damping expression [5] you can see the effect of increasing RS. If RS is increased to the point where it equals the characteristic impedance of the line (RS = sqrt(L/(2*C1)) then the line damps itself even with CL = 0. That's the benefit of raising RS. The higher you make RS the more natural damping you get. The lower you make RS the harder you have to work to damp the line elsewhere (i.e., by making CL larger or by adding other termination components).
（4） Capacitances in the middle range between these two extremes [4] and [5] cause the worst problems with ringing and overshoot.