


哈希表也有一些缺点它是基于数组的,数组创建后难于扩展某些哈希表被基本填满时,性能下降得非常严重,所以程序虽必须要清楚表中将要存储多少数据(或者准备好定期地把数据转移到更大的哈希表中,这是个费时的过程)。
而且,也没有一种简便的方法可以以任何一种顺序〔例如从小到大〕遍历表中数据项。如果需要这种能力,就只能选择其他数据结构。
然而如果不需要有序遍历数据,井且可以提前预测数据量的大小。那么哈希表在速度和易用性方面是无与伦比的。
哈希表算法-哈希表的概念及作用
一般的线性表,树中,记录在结构中的相对位置是随机的,即和记录的关键字之间不存在确定的关系,因此,在结构中查找记录时需进行一系列和关键字的比较。这一类查找方法建立在“比较“的基础上,查找的效率依赖于查找过程中所进行的比较次数。
理想的情况是能直接找到需要的记录,因此必须在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使每个关键字和结构中一个唯一的存储位置相对应。
哈希表最常见的例子是以学生学号为关键字的成绩表,1号学生的记录位置在第一条,10号学生的记录位置在第10条...
如果我们以学生姓名为关键字,如何建立查找表,使得根据姓名可以直接找到相应记录呢?
用上述得到的数值作为对应记录在表中的位置,得到下表:
上面这张表即哈希表。
如果将来要查李秋梅的成绩,可以用上述方法求出该记录所在位置:
李秋梅:lqm 12+17+13=42 取表中第42条记录即可。
问题:如果两个同学分别叫 刘丽 刘兰 该如何处理这两条记录?
这个问题是哈希表不可避免的,即冲突现象:对不同的关键字可能得到同一哈希地址。
哈希表算法-哈希表的构造方法
1、直接定址法
例如:有一个从1到100岁的人口数字统计表,其中,年龄作为关键字,哈希函数取关键字自身。
但这种方法效率不高,时间复杂度是O(1),空间复杂度是O(n),n是关键字的个数
2、数字分析法
有学生的生日数据如下:
年.月.日
75.10.03
75.11.23
76.03.02
76.07.12
75.04.21
76.02.15
...
经分析,第一位,第二位,第三位重复的可能性大,取这三位造成冲突的机会增加,所以尽量不取前三位,取后三位比较好。
3、平方取中法
取关键字平方后的中间几位为哈希地址。
4、折叠法
将关键字分割成位数相同的几部分(最后一部分的位数可以不同),然后取这几部分的叠加和(舍去进位)作为哈希地址,这方法称为折叠法。
例如:每一种西文图书都有一个国际标准图书编号,它是一个10位的十进制数字,若要以它作关键字建立一个哈希表,当馆藏书种类不到10,000时,可采用此法构造一个四位数的哈希函数。如果一本书的编号为0-442-20586-4,则:
5、除留余数法
取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址。
H(key)=key MOD p (p<=m)
6、随机数法
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即
H(key)=random(key) ,其中random为随机函数。通常用于关键字长度不等时采用此法。
5、除留余数法
取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址。
H(key)=key MOD p (p<=m)
6、随机数法
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即
H(key)=random(key) ,其中random为随机函数。通常用于关键字长度不等时采用此法。
5、除留余数法
取关键字被某个不大于哈希表表长m的数p除后所得余数为哈希地址。
H(key)=key MOD p (p<=m)
6、随机数法
选择一个随机函数,取关键字的随机函数值为它的哈希地址,即
H(key)=random(key) ,其中random为随机函数。通常用于关键字长度不等时采用此法。
哈希表算法-处理冲突的方法
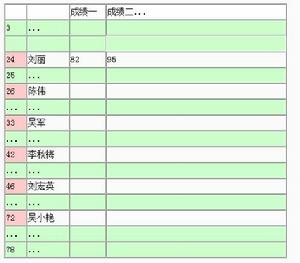
如果两个同学分别叫 刘丽 刘兰,当加入刘兰时,地址24发生了冲突,我们可以以某种规律使用其它的存储位置,如果选择的一个其它位置仍有冲突,则再选下一个,直到找到没有冲突的位置。选择其它位置的方法有:
1、开放定址法
Hi=(H(key)+di) MOD m i=1,2,...,k(k<=m-1)
其中m为表长,di为增量序列
如果di值可能为1,2,3,...m-1,称线性探测再散列。
如果di取值可能为1,-1,2,-2,4,-4,9,-9,16,-16,...k*k,-k*k(k<=m/2)
称二次探测再散列。
如果di取值可能为伪随机数列。称伪随机探测再散列。
例:在长度为11的哈希表中已填有关键字分别为17,60,29的记录,现有第四个记录,其关键字为38,由哈希函数得到地址为5,若用线性探测再散列,如下:
2、再哈希法
当发生冲突时,使用第二个、第三个、哈希函数计算地址,直到无冲突时。缺点:计算时间增加。
3、链地址法
将所有关键字为同义词的记录存储在同一线性链表中。
4、建立一个公共溢出区
假设哈希函数的值域为[0,m-1],则设向量HashTable[0..m-1]为基本表,另外设立存储空间向量OverTable[0..v]用以存储发生冲突的记录
例如,按上面例9.4所给的关键字序列,用拉链法构造散列表如图9.14所示。
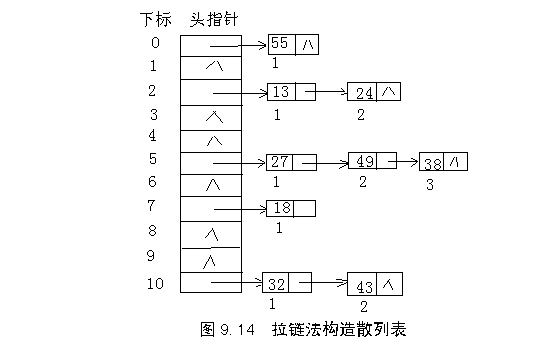
用拉链法处理冲突,虽然比开放定址法多占用一些存储空间用做链接指针,但它可以减少在插入和查找过程中同关键字平均比较次数(平均查找长度),这是因为,在拉链法中待比较的结点都是同义词结点,而在开放定址法中,待比较的结点不仅包含有同义词结点,而且包含有非同义词结点,往往非同义词结点比同义词结点还要多。
如前面介绍的例9.4中,用线性探测法构造散列表的过程,我们知道,对前5个关键字的查找,每一个仅需要比较一次,对关键字49和24的查找,则需要比较2次,对关键字38的查找则需要比较4次,而对43的查找则需要比较3次。因此,对用线性探测法构造的散列表的平均查找长度为:
ASL=(1×5+2×2+3×1+4×1)/9 ≈1.78
而用拉链法构造的散列表上查找成功的平均查找长度为:
ASL=(1×5+2×3+3×1)/9≈1.55
显然,开放定址法处理冲突的的平均查找长度要高于拉链法处理冲突的平均查找长度。但它们都比前面介绍的其它查找方法的平均查找长度要短。
|
|
作者: 李肖遥, 来源:面包板社区
链接: https://mbb.eet-china.com/blog/uid-me-3912462.html
版权声明:本文为博主原创,未经本人允许,禁止转载!
 /4
/4 
文章评论(0条评论)
登录后参与讨论