


相信很多小伙伴都用过下面这个MOS管开关电路,但是有多少小伙伴了解在MOS管开关过程中,输入电压、输出电压和MOS管上的电流都是怎么变化的?特别是输出端有大负载电容时,最大浪涌电流能到多少呢?
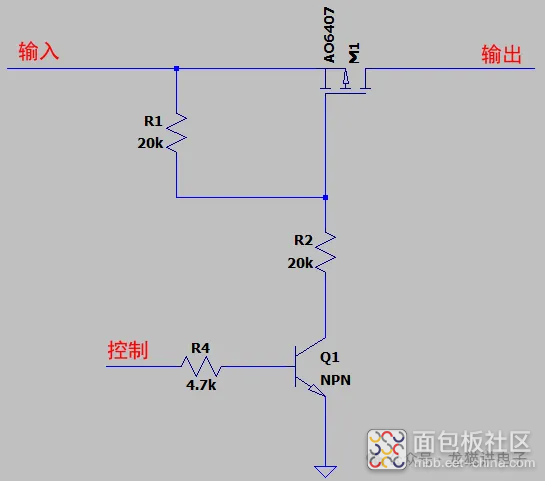
今天小编专门写一篇文章,通过理论结合仿真的方式给大家分析下~
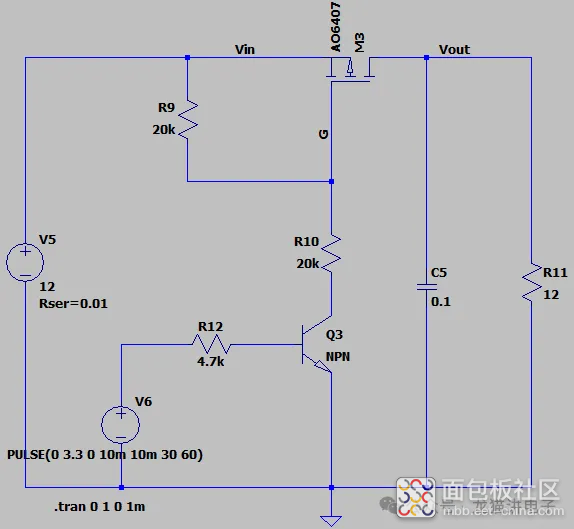
首先建立一个电路图:假定电源电压V5=12V,内阻Rs=10毫欧;MOS管的导通与关闭由$V_6$控制;负载设定为100mF电容+$12\Omega$电阻。
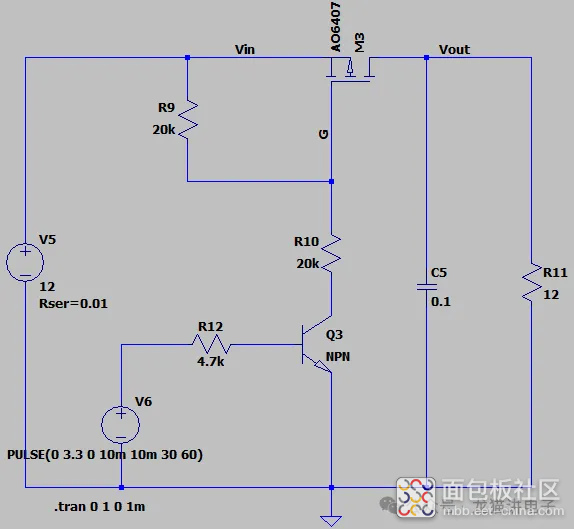
上升阶段
当控制信号输出高电平时,$V_6$电压会逐渐上升,当电压上升到三极管$Q_3$的门槛电压,三极管开始导通;按照Paul R. Gray著作《Analysis and Design of Analog Integrated Circuits》中推导,三极管集电极电流可写成:
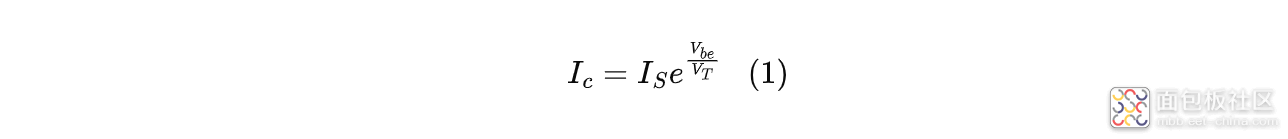
式中:$I_S$为反向饱和电流;$V_T$为热电压,常温下约为26mV;$V_{be}$为三极管基极-发射极电压;
根据MOS管开关电路,MOS管栅源电压为:
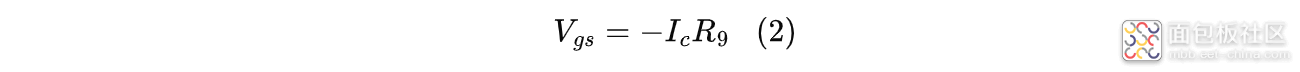
栅源电压$V_{gs}$会随着$I_c$的增加逐渐变大,当$V_{gs}$达到MOS管的阈值电压$V_{gs{th}}$时,MOS管开始导通,漏极电流开始增加;此时输出电压$V_{out}$很小,所以$V_{sd}$接近于输入电压$V_{in}$,MOS管工作在恒流区,MOS管电流满足下式:
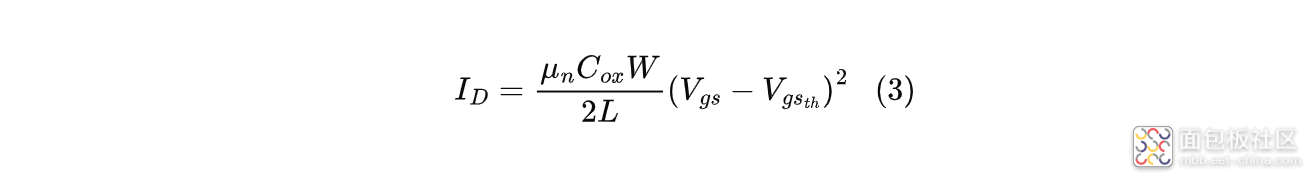
式中:$\mu_n$是电子迁移率;$C_{ox}$是单位面积栅极电容;$W$是沟道宽度;$L$是沟道长度;$V_{gs}$是栅极与源极之间的电压;$V_{gs_{th}}$是阈值电压。
随着三极管的基极电压升高,$I_c$成指数倍增加;同理$V_{gs}$也成指数倍增加,所以通过MOS管的电流会快速上升。
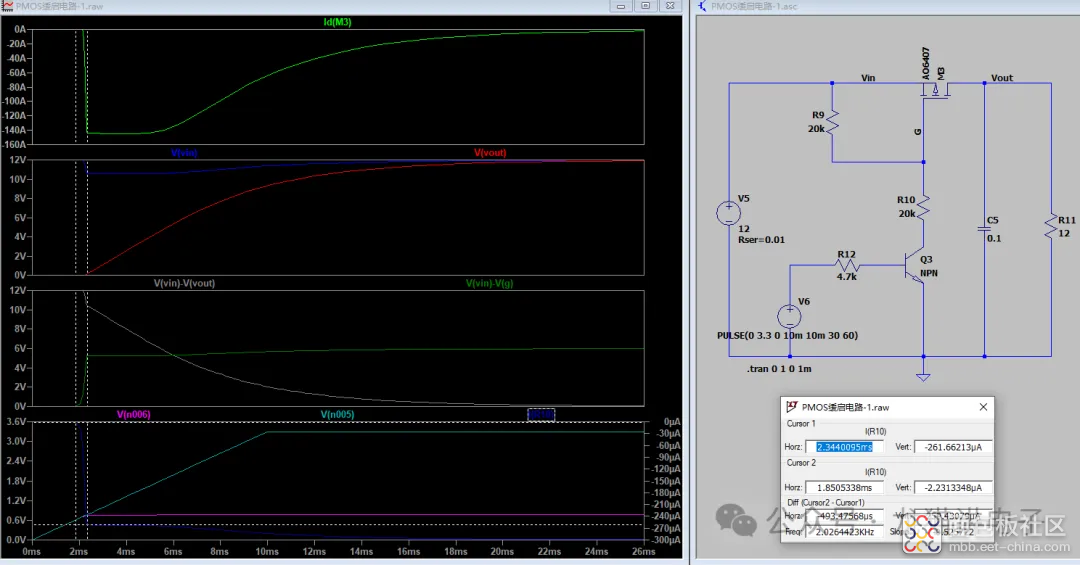
直到三极管进入饱和区,此时$V_{CE}\approx0V$,MOS管的栅源电压达到理论最大值$V_{gs_{max}}$,通过MOS管的电流也达到最大值$I_{max}$。
因为小编建立的仿真模型中,电源是有内阻的,所以实际上$V_{gs_{max}}$的值应为:
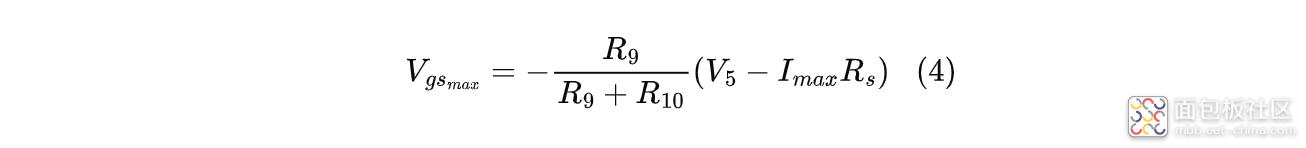
而$I_{max}R_s$正是MOS管开启造成的电压跌落,若电压跌落过大,可能会导致其他电路工作异常。
但很快小编就发现,因为$\mu_n$、$C_{ox}$、$W$、$L$参数的缺失,导致无法计算峰值浪涌电流$I_{max}$,那还有其他计算方式吗?
答案是:有的,并且被小编找到了。
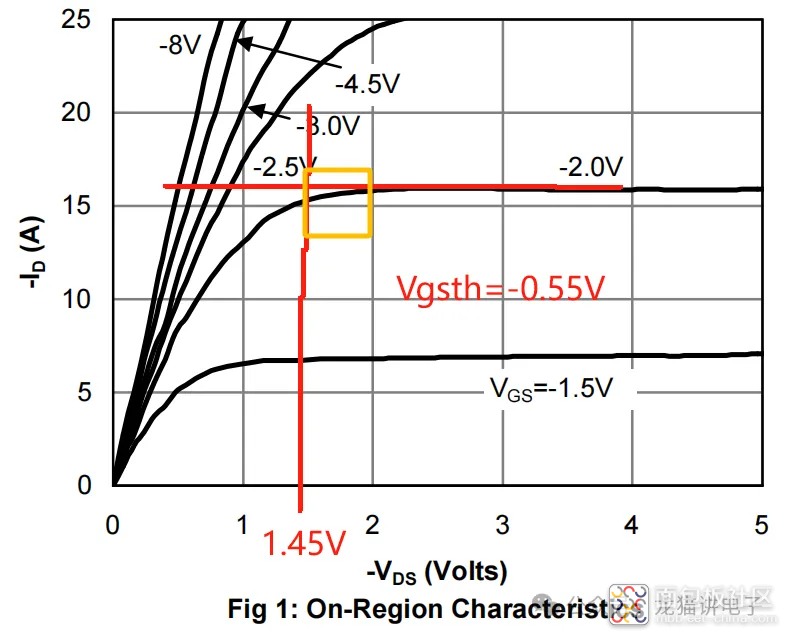
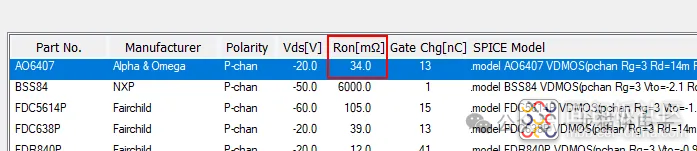
首先,找到MOS管的输出特性曲线图,可以轻松获得$V_{gs}=1.5V$或其他值时所对应的漏极饱和电流$I_{D_1}$;
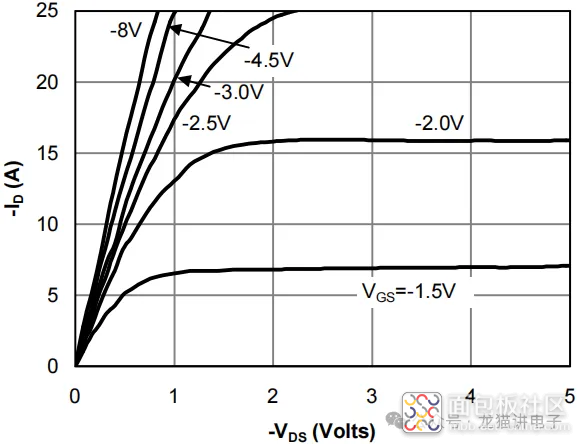
然后代入到式(3)中(这里小编取$V_{GS}=-1.5V$,$I_{D_1}=7A$(预估值),$V_{gs_{th}}=-0.55V$(规格书读取)):
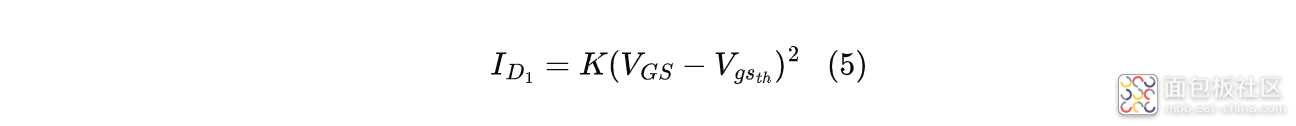
计算出$K=7.76$
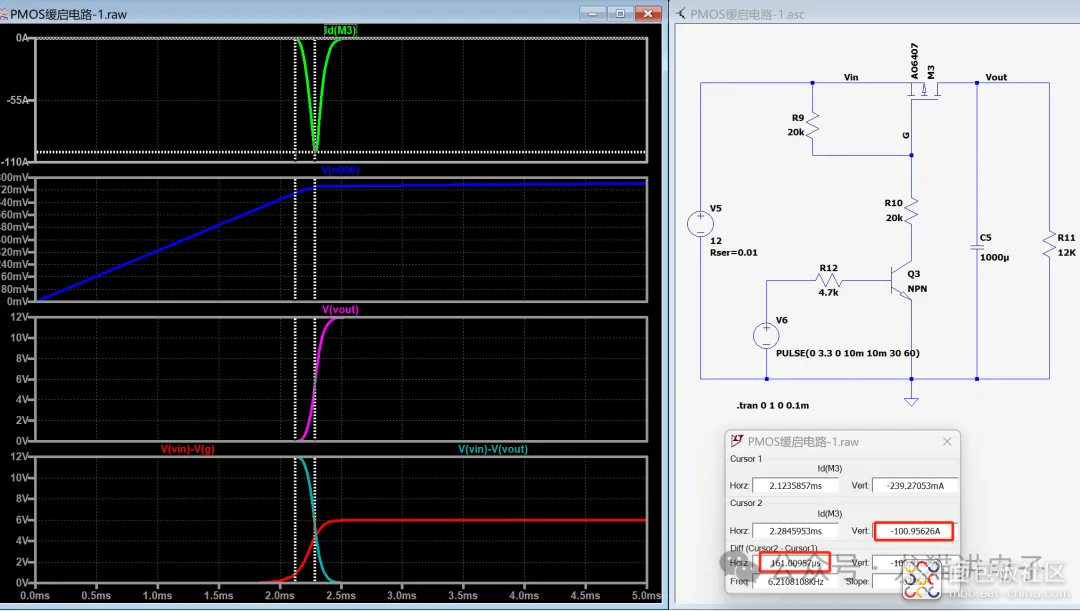
最后再将计算出来的系数$K$代回式(3)、(4),计算出$I_{max}=152.73A$,$V_{gs}=-5.24V$,基本接近仿真结果。
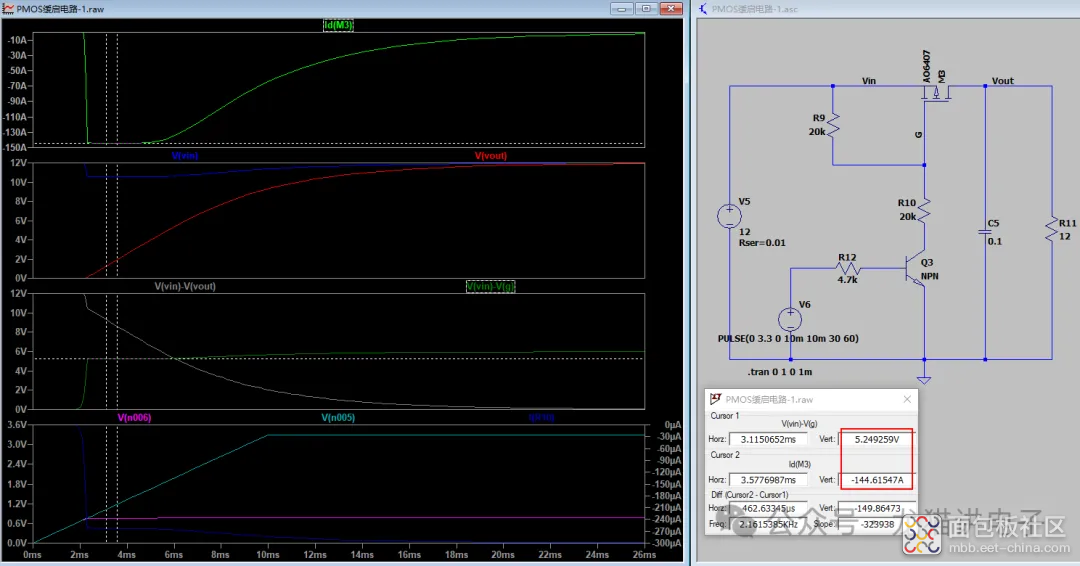
因为仿真模型中阈值电压等于-0.8V,所以上述计算过程中是以$V_{gs_{th}}=-0.8V$计算的。

推导出最大浪涌电流的计算公式,小编还想知道下上升过程总共用了多长时间?
在三极管达到饱和状态前,$Q_3$一直工作在放大区,所以有:
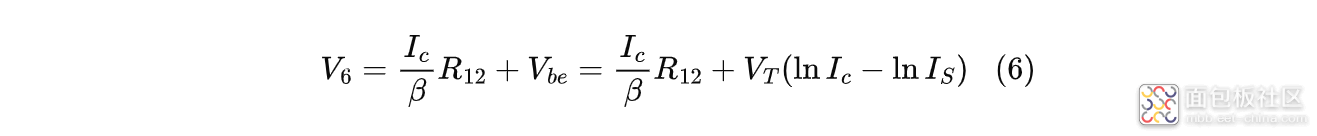
式中:$\beta$为三极管的放大倍数;$I_S$为反向饱和电流;$V_T$为热电压,常温下约为26mV;
对于$V_6$控制信号,在上升沿10%~90%内,完全可以考虑成线性, 所以假设$V_6=at$,则:
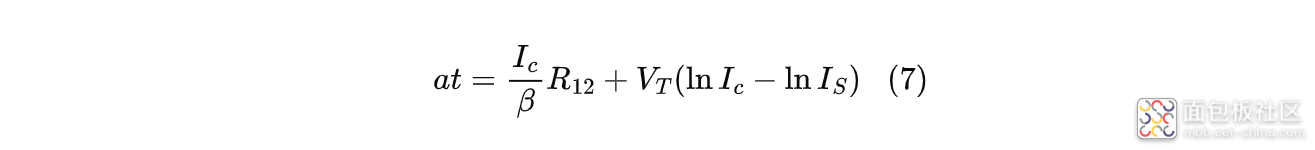
MOS管电流上升所用的时间其实就是栅源电压从$V_{gs_{th}}$(对应t1)上升到$V_{gs_{max}}$(对应t2)的时间,所以联合式(2)、(7)可得:
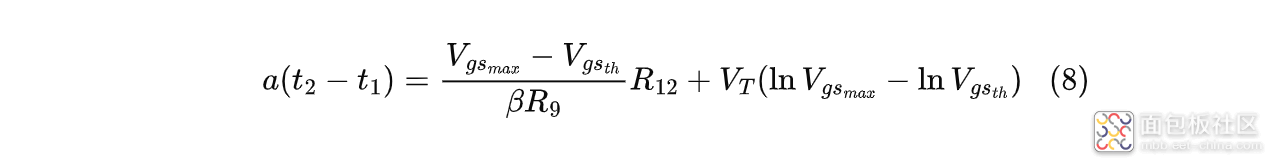
所以只要知道斜率a,就可以计算出电流上升过程的时间。
恒流阶段
当三极管$Q_3$饱和后,$V_{gs}=-\frac{R_9}{R_9+R_{10}}V_{in}$,若此时$V_{in}$恒定,则$V_{gs}$和漏极电流$I_D$也恒定;漏极电流$I_D$恒定,则$V_{in}$保持恒定,所以此时会出现一段恒流过程。
在此阶段,通过MOS管的电流会持续给负载电容充电,所以$V_{out}$会线性上升,$V_{ds}$会线性下降。
当$|V_{ds}|< |V_{gs}-V_{gs_{th}}|$时,漏极电流将按照下式计算:
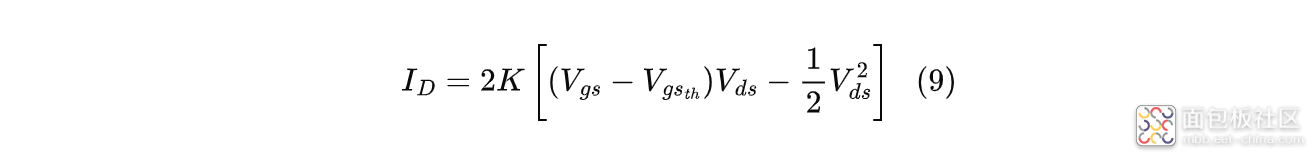
然后漏极电流$I_D$会随着$V_{ds}$的减小而逐渐减小;从而退出恒流阶段,进入电流下降阶段。
恒流阶段的总时长可以根据负载电容的充电来计算:
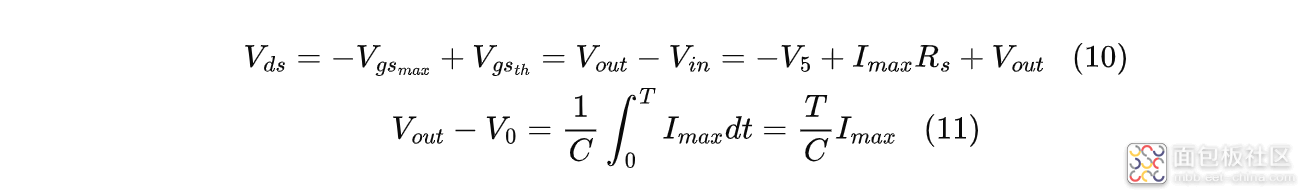
式中:$V_0$是进入恒流时的输出电压;$C$是负载电容的容值;
最终再结合上升阶段求解的$I_{max}$,可以计算出恒流阶段的时长:
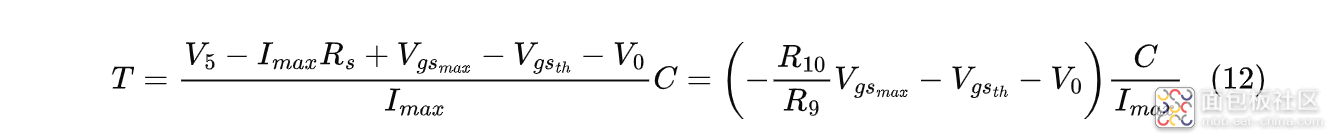
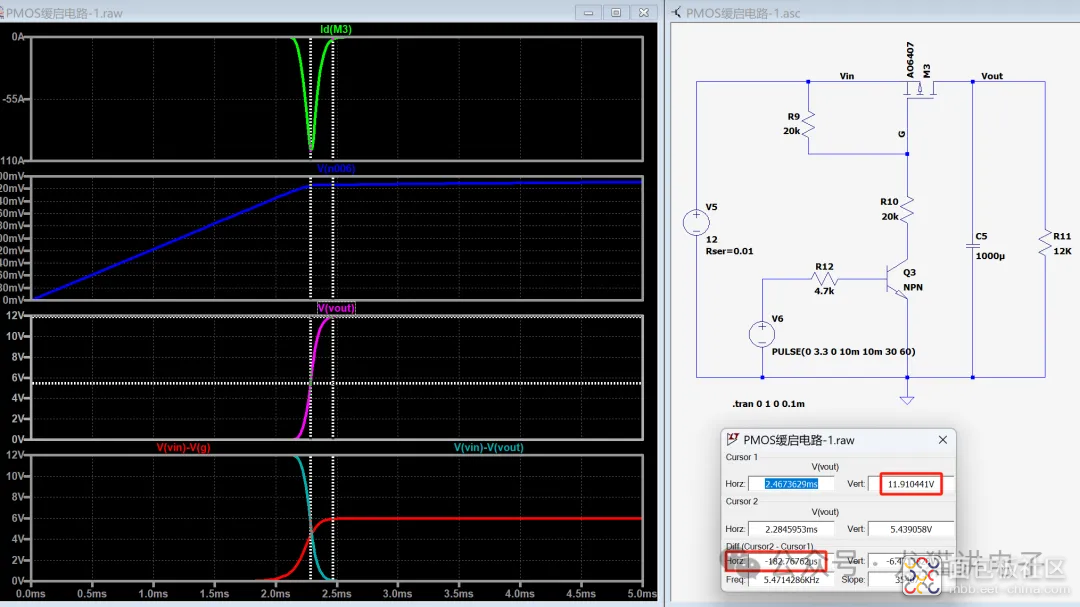
当负载电容较大时,可近似地认为$V_0=0V$,采用仿真模型中的值,计算出$T=3.95ms$,还是比较接近于仿真模型。
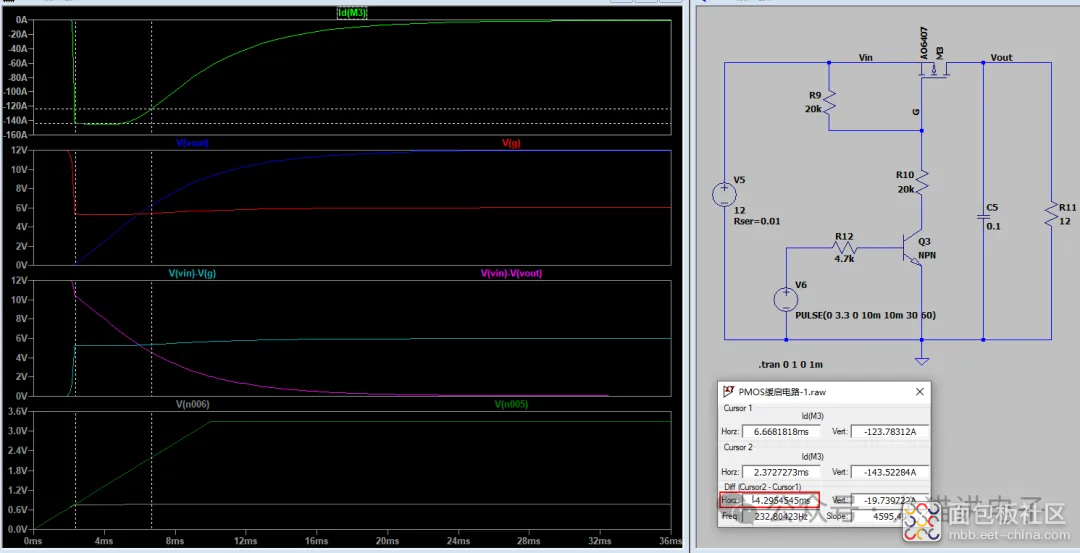
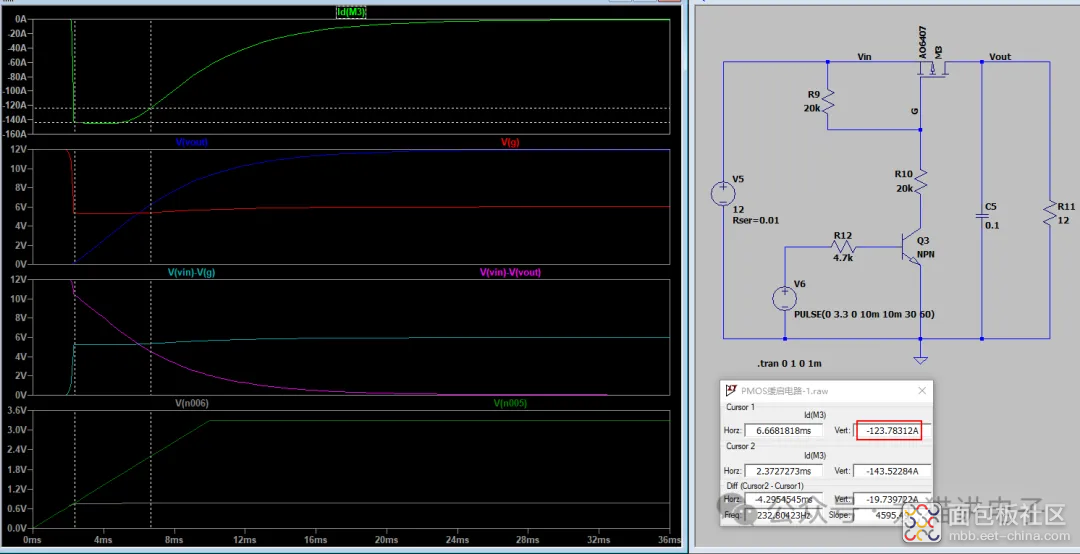
小编认为,理论值与仿真值存在差异原因是:当$V_{ds}$接近于$V_{gs}-V_{gs_{th}}$时,通过MOS管的电流会减小(如下图黄框区域),从而导致$V_{ds}$下降速率减缓,延长了时间;换句话说,就是MOS管的电流公式过于理想,存在一些偏差。
可能有的小伙伴也注意到了,小编在仿真电路中选取的负载电容非常大,这主要是为了让小伙伴们看到恒流阶段;其实在不同的MOS管或较小的负载电容的情况下,如果在$V_{gs}$达到最大之前就出现$V_{ds}=V_{gs}-V_{gs_{th}}$,那么就不会存在恒流阶段。
并且根据恒流区出现条件可以得出以下结论:
1. 负载电容越大,输出电压上升越慢,$V_{ds}$下降越慢,越容易出现恒流区;
2. 控制信号上升时间越短,$V_{gs}$上升越快,越容易出现恒流区;
3. $V_{gs_{max}}$越小,峰值浪涌电流越小,越容易出现恒流区;
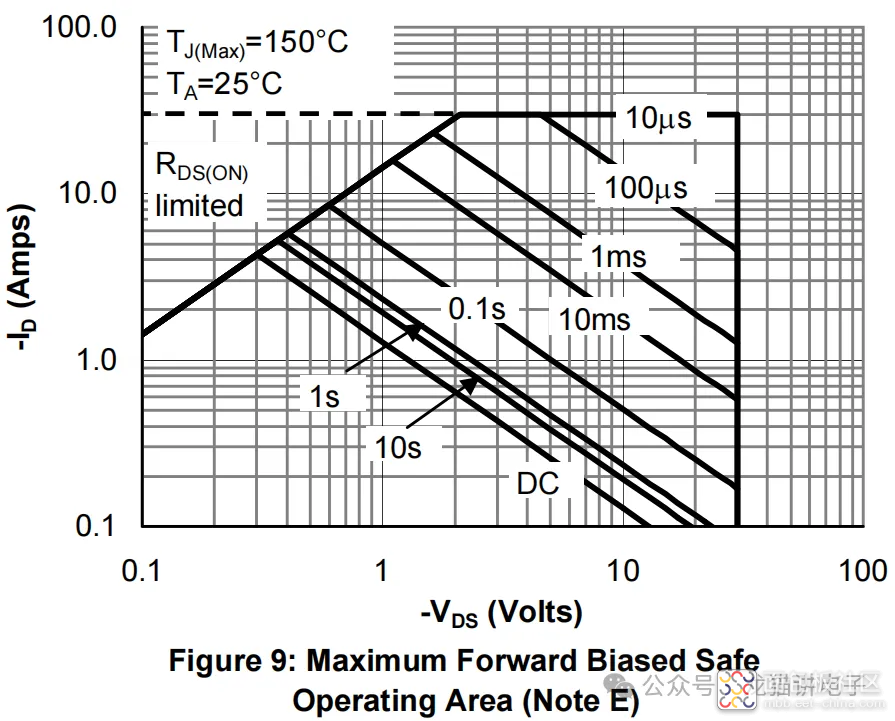
其实在大多数电路中并不会出现恒流阶段,或者说根本不允许出现恒流阶段:这是AO6407的输出特性曲线图,我们可以看到当$V_{gs}=-2V$时,其恒流区电流已经超过15A;在$V_{gs}=-2.5V$时,更是超过25A;而根据其SOA图可知,AO6407所能承载的最大电流值为30A。
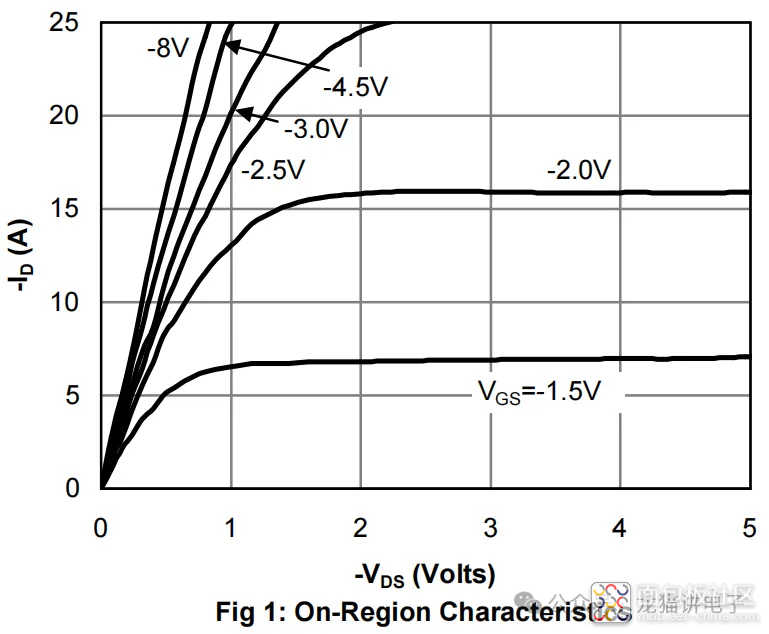
所以若MOS管开启过程真的存在恒流阶段,那么其$V_{gs}$不能超过2.5V,此时将很容易满足$V_{ds}=V_{gs}-V_{gs_{th}}$。
当不存在恒流阶段时,峰值浪涌电流又该如何计算呢?
假设在T时刻达到$V_{ds}=V_{gs}-V_{gs_{th}}$,此时栅源电压为$V_{gs}'$,源漏电压为$V_{ds}'$,通过MOS管的电流为$I_{max}$,则:
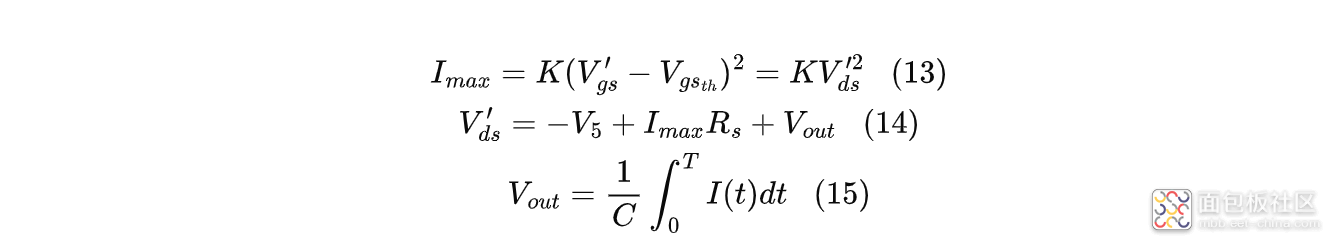
当电流$I$上升较快时,可以认为电流$I$的上升斜率固定,此时有:
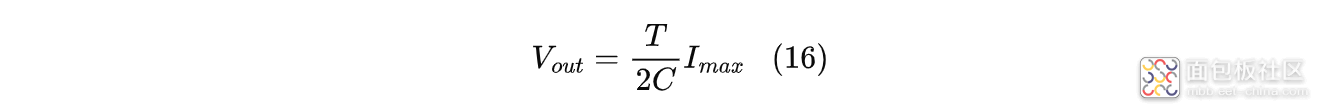
整理得:
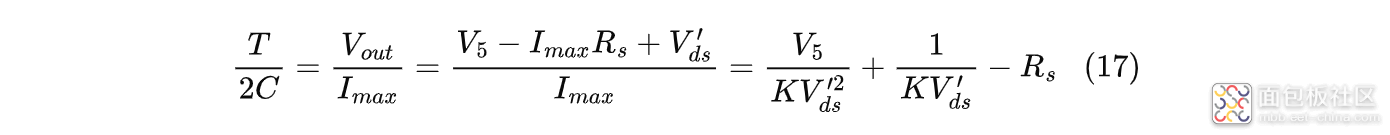
令$X=\frac{1}{V_{ds}'}$,简化式(21)得:
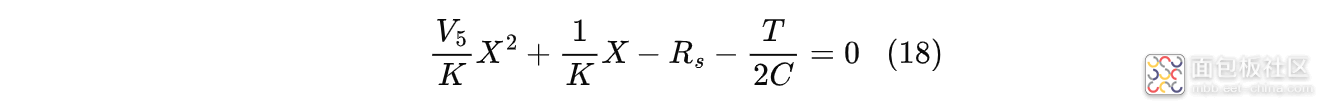
求解得:
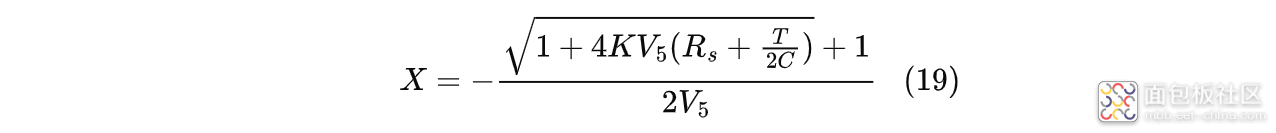
即:
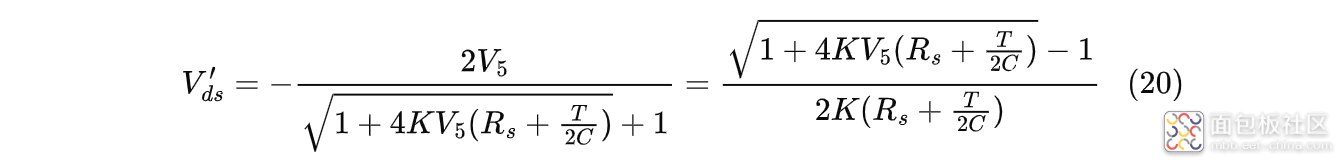
公式较为复杂,这里通过实例举证来给各位小伙伴一个概念:假定$T=320us$、$C=10mF$,$K$、$V_5$、$R_s$仍然采用仿真电路中的参数,代入式(24),求解出:$V_{ds}'=5.62V$,$I_{max}=245.3A$。
在上述公式推导过程中,针对$V_{out}$的求解,小编是采用积分的方式,然后等效成三角形面积;正常来讲,因为MOS管的非理想化,这种方式会有一些偏差;
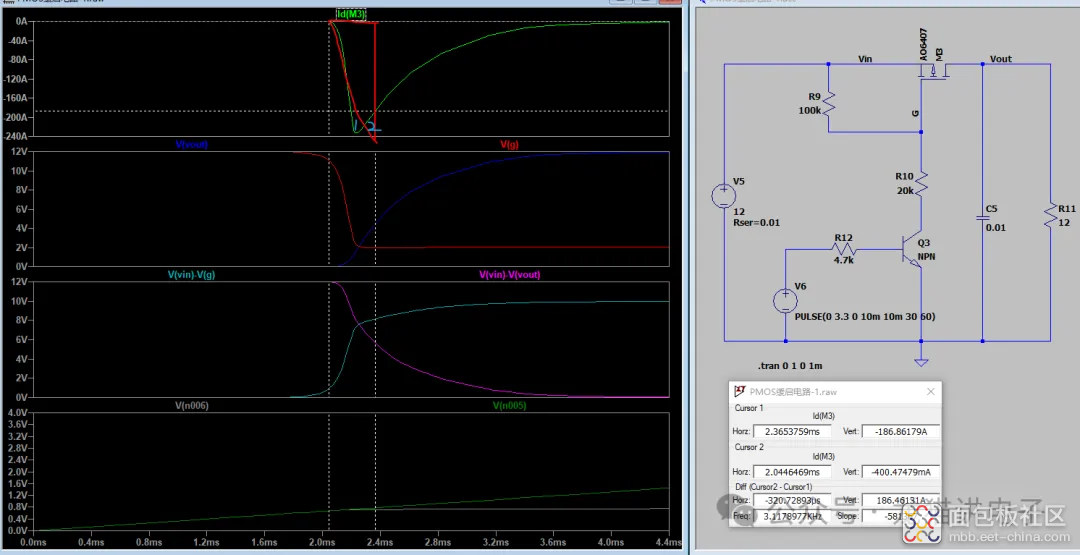
但是巧合的是,如果以$I_{max}$来建立三角形,其实面积偏差很小;而且$V_{ds}'$代入式(17)计算出来的电流值也刚好是下降前的饱和电流值;所以最终用式(20)和式(13)计算出来的峰值浪涌电流其实很接近于实际值。
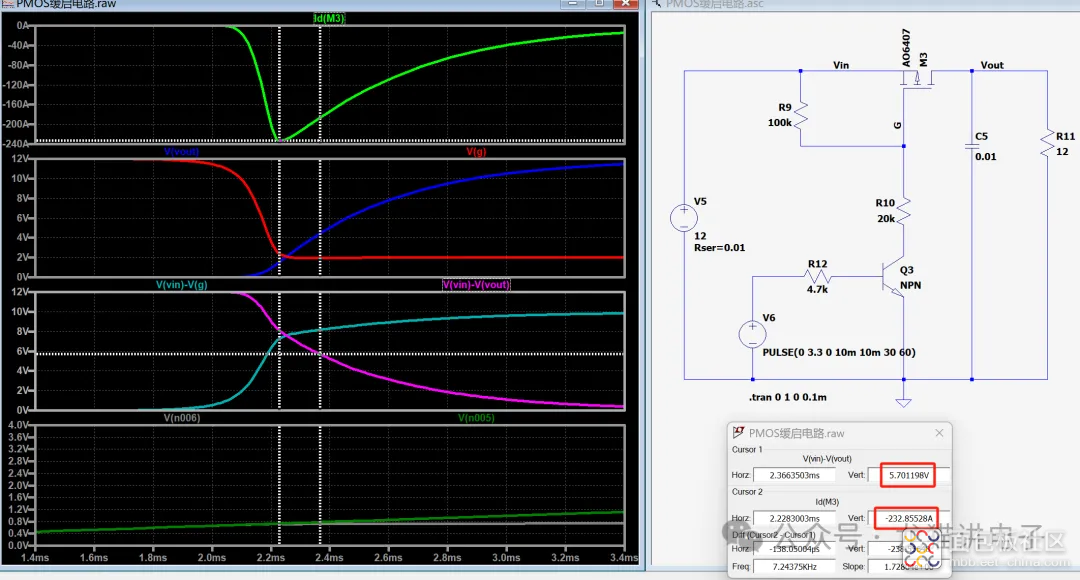
上述计算中$T$是通过仿真波形中读取的,在实际评估中可以再联立式(8)进行求解。
下降阶段
当$V_{ds}< (V_{gs}-V_{gs_{th}})$,漏极电流$I_D$进入下降阶段,此时可认为MOS管工作在恒阻区;
在该阶段,电源$V_5$会通过内阻$R_s$和MOS管的导通电阻$R_{ON}$持续给负载电容充电,所以此阶段的时长可以根据电容充电公式计算:
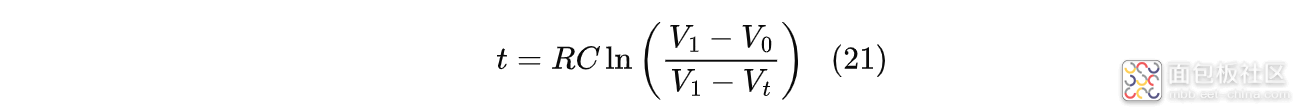
式中:$R$为电源内阻$R_s$和MOS管导通电阻$R_{ON}$的和;$V_0$为此阶段电容两端电压的初始值;$V_1$为电容最终可充到或放到的电压值;$V_t$为t时刻电容两端的电压值。
另外,从恒流阶段与下降阶段的过渡点,小编又找到一个计算最大浪涌电流的公式,在过渡点上满足:
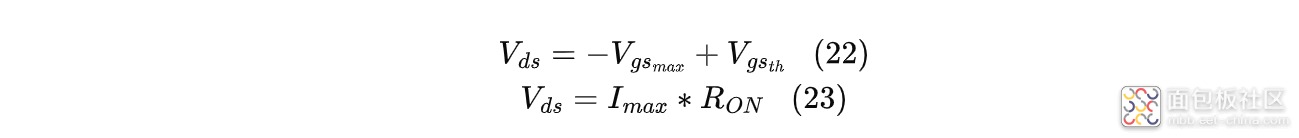
整理式(11)、(12)得:
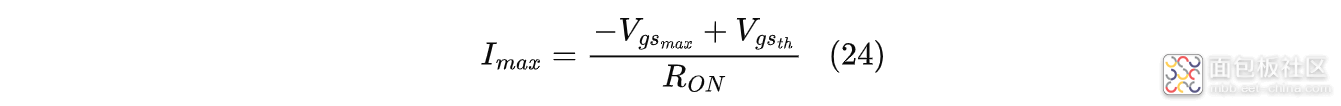
用仿真模型中MOS管的导通电阻和阈值电压代入式(13),计算出:$I_{max}=130.88A$,也接近于仿真结果;同样,因为MOS管的非理想化,通过式(24)计算的电流值会比实际峰值浪涌电流偏低。
结合式(12)和式(24)可简化恒流区的时长公式:
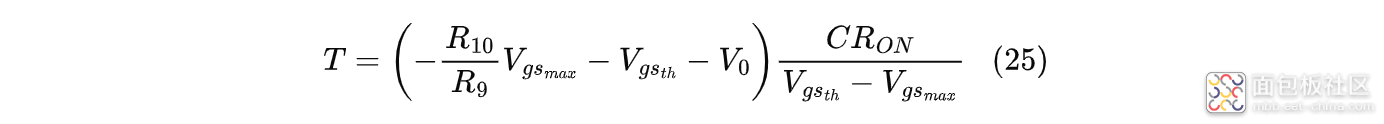
从式(25)、(26)可以看出,当降低$V_{gs_{max}}$时,峰值浪涌电流也会随着变小;但是恒流阶段的持续时间将会增加。
总结
MOS管开启过程可以根据MOS管电流的变化分成三个阶段:上升阶段、恒流阶段和下降阶段;但在实际电路中基本只有上升和下降两个阶段。
判断是否会出现恒流阶段也比较简单,可以先假设不出现,然后用式(20)计算出此时的$V_{ds_1}$,如果$|V_{ds_1}|>|V_{gs_{max}}-V_{gs_{th}}|$,则说明存在恒流阶段;式(20)如下:
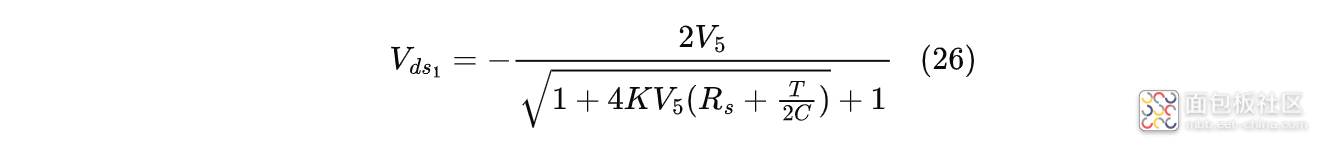
式中:$K$为描述MOS管电流驱动能力的系数,可通过MOS管的输出特性曲线图求解;$V_5$为输入电压;$R_s$为输入电源内阻;$C$为负载电容;$T$为漏源电压从$V_5$降到$V_{ds_1}$的时长;
如果存在恒流阶段,MOS管峰值电流计算公式为:
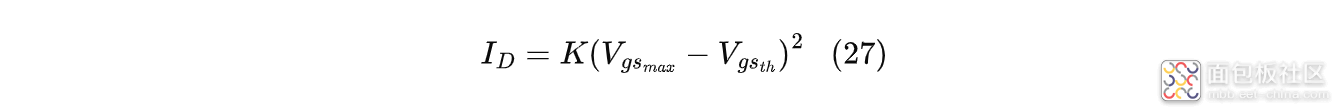
式中:$K$为描述MOS管电流驱动能力的系数;$V_{gs_{max}}$为栅源电压最大值;$V_{gs_{th}}$为MOS管的阈值电压;
或者:
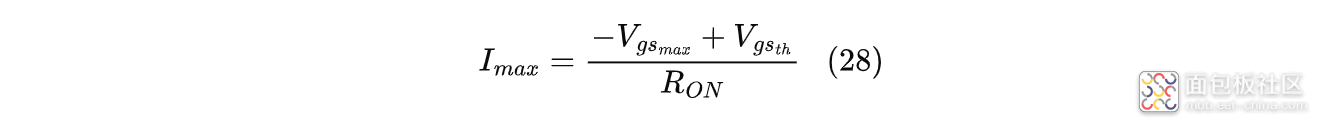
式中:$V_{gs_{max}}$为栅源电压最大值;$V_{gs_{th}}$为MOS管的阈值电压;$R_{ON}$为MOS管的导通电阻;
如果不存在恒流阶段,MOS管峰值电流计算公式为:
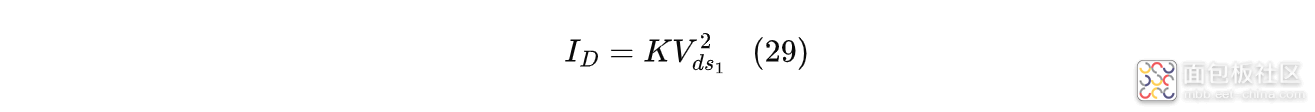
式中:$K$为描述MOS管电流驱动能力的系数;
MOS管电流从零上升到峰值电流的总时间可用下式计算:
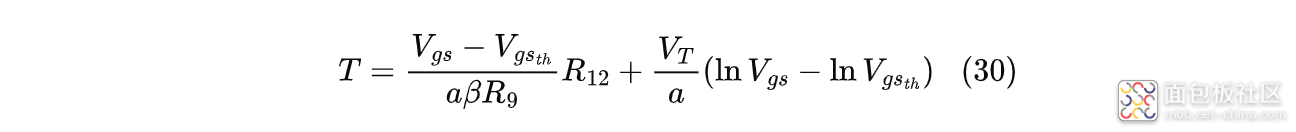
式中:$V_{gs}$为峰值电流所对应的栅源电压;$\beta$为三极管放大倍数;$V_{gs_{th}}$为MOS管的阈值电压;$R_{12}$为基极限流电阻;$R_9$为分压电路中的上电阻(栅源间);$V_T$为热电压,常温下约为26mV;$a$为控制信号上升沿的斜率;
如果存在恒流阶段,其维持时间可用如下公式估算:
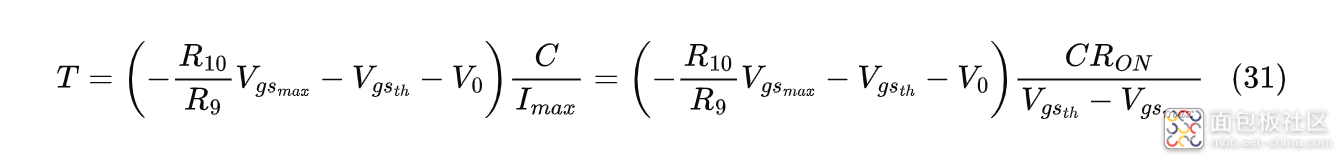
式中:$R_{10}$为分压电路中的下电阻(栅极与地之间);$R_9$为分压电路中的上电阻(栅源间);$V_{gs_{max}}$为栅源电压最大值;$V_{gs_{th}}$为MOS管的阈值电压;$C$为负载电容;$R_{ON}$为MOS管的导通电阻。
而下降阶段的总时长可用下式计算:
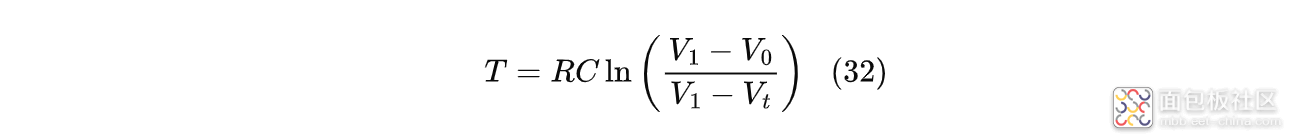
式中:$R$为电源内阻$R_s$和MOS管导通电阻$R_{ON}$的和;$V_0$为下降阶段开始时的输出电压,可用式(15)(有恒流阶段)或式(26)(无恒流阶段)计算;$V_1$为最终可充到的输出电压;$V_t$为$T$时刻的输出电压。
为了方便计算,小编将上述公式整理到Excel表格中,与仿真电路对比,结果虽有偏差(造成偏差的原因,小编在文中已经介绍过),但经过小编多组数据验证,结果基本在同量级,用来评估电路特性,小编认为基本够用了~
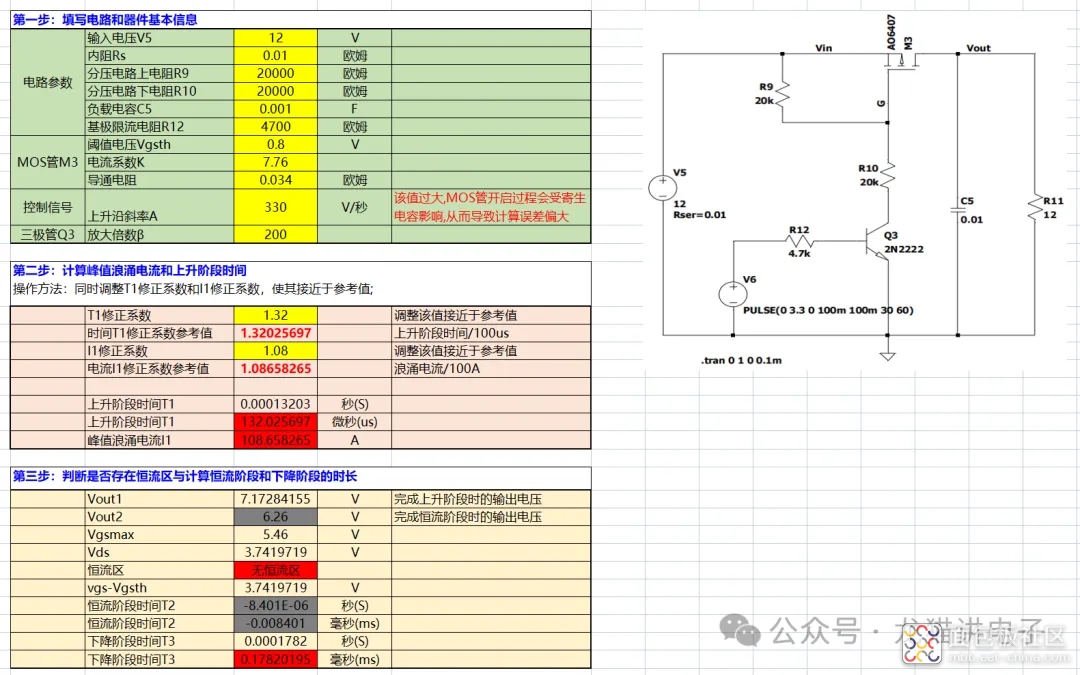
有需要的小伙伴可以关注微信公众号:龙猫讲电子,然后在后台回复:工具 | MOS管开关电路峰值浪涌电流计算工具
本文所述观点仅为小编个人见解,在此抛砖引玉,若存在任何疏漏或错误之处,恳请各位读者不吝赐教。
声明:本号对所有原创、转载文章的陈述与观点均保持中立,推送文章仅供读者学习和交流。文章、图片等版权归原作者享有,如有侵权,联系删除。
作者: 龙猫讲电子, 来源:面包板社区
链接: https://mbb.eet-china.com/blog/uid-me-4049683.html
版权声明:本文为博主原创,未经本人允许,禁止转载!
开发工匠 2025-5-10 11:47
龙猫讲电子 2025-4-19 08:19
luckyzy2000 2025-4-18 14:36
开发工匠 2025-4-15 12:01
eeNick 2025-4-14 09:35