仍然使用FDATOOL设计滤波器,当前设计一个数字带通滤波器。至于用的是冲击响应不变法,还是其它的方法。暂时不考虑。FIR 需要的阶数太多,也不考虑。使用IIR滤波,线性相位就不要想了。可以选巴特沃兹(最大平整度),或切比雪夫(最大陡降特性。)发现在相同的性能下切比雪夫需要的阶数少。
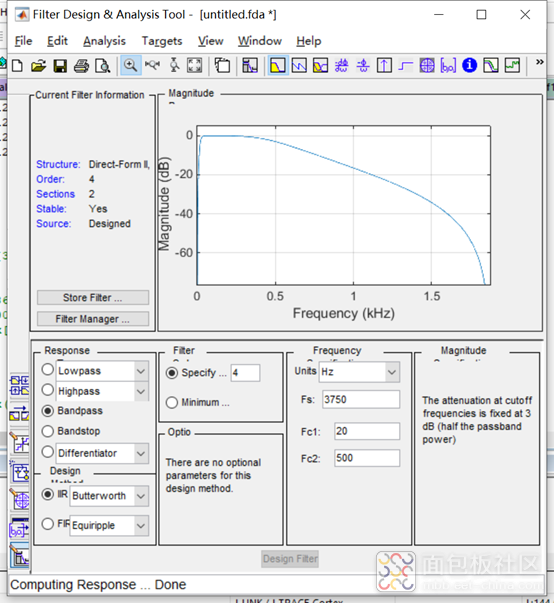
生成的传递函数是按照多个二阶单元级联。系统提供 SOS(Second Order Section)也可以称为“救命”矩阵。其思路是将高阶传递函数分解为多个稳定的二阶函数级联,保持系统稳定。因为使用的是IIR (无限冲击响应)构成,注定其是非线性相位。会导致滤波后的信号波形畸变。导出滤波器参数文件.
% Generated by MATLAB(R) 8.4 and the Signal Processing Toolbox 6.22.
% Generated on: 04-Jun-2022 20:49:14 % Coefficient Format: Decimal % Discrete-Time IIR Filter (real) % ------------------------------- % Filter Structure : Direct-Form II, Second-Order Sections% Number of Sections : 2 % Stable : Yes % Linear Phase : No SOS Matrix: 1 0 -1 1 -1.9528158412163148 0.95399450820943588 1 0 -1 1 -0.92310027138083539 0.34076352170725532 Scale Values: 0.31856548677578983 0.31856548677578983 复制代码
每个SOS参数可以使用直接II型,实现如下:
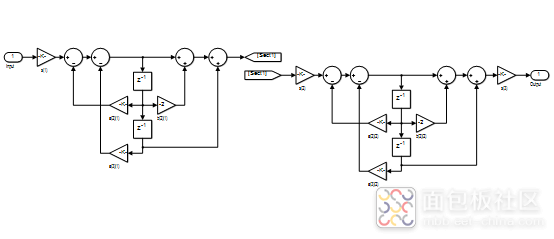
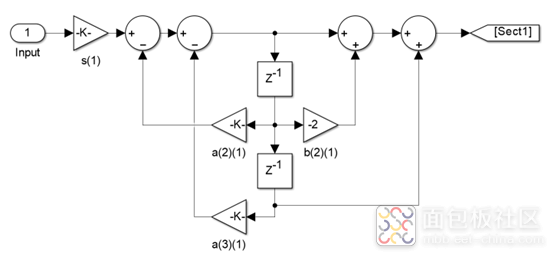
编写一段代码测试一下。
clear
close all Fs = 30000; % Sampling Frequency % 20-500 30000sps butter 4 ordersec = 2;SOS = [1 0 -1 1 -1.9941159332576488 0.99413480892694572;1 0 -1 1 -1.8630805194585167 0.87259004111123051];G = [0.048551094455762382 0.048551094455762382 1]; len = Fs/10; % Êý¾Ý³¤¶ÈΪ 100mSt = 1:len;n = 300*sin(2*pi*15*t/Fs + pi/6); % 50hz noises = 3000*sin(2*pi*200*t/Fs + pi/5); % original square wave signalng = 500*randn(1,len);x = s + n + + ng + 1000;fftx = abs(fft(x,len));f = 0:Fs/len:(len-1)*(Fs/len);figure(1)plot(f(1:len/20),fftx(1:len/20))title('sinc fuction spectrum') w = zeros(sec,3);ym = zeros(1,sec+1);for i = 1:len ym(1) = x(i); for k = 1:sec w(k,1) = ym(k) * G(k) - w(k,2) * SOS(k,5) - w(k,3) * SOS(k,6) ym(k+1) = w(k,1)*SOS(k,1)+w(k,2)*SOS(k,2)+w(k,3)*SOS(k,3); w(k,3) = w(k,2); w(k,2) = w(k,1); end y(i) = ym(sec+1)*G(sec+1);end figure(2)plot(t,s,'r',t,x,'c',t,y,'.b')legend('signal','org','bandpass');复制代码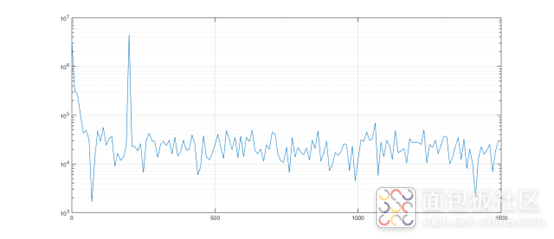
待滤波信号的频谱特性
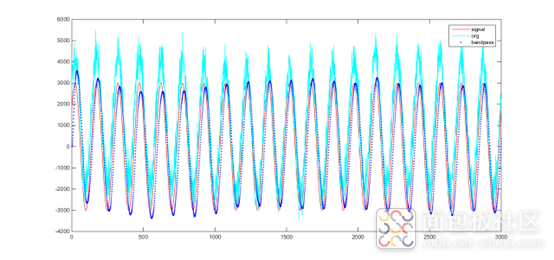
可以看到org 信号上有噪声,有直流偏置和低频交流干扰。经过带通滤波后,去除了直流,去除了噪声,基本还原原始信号signal。刚开始时并不稳定需要等一段时间才能达到稳定。
可见,此段代码可以将一个输入序列x 转换为一个输出序列 y,完成对x序列的滤波。
按照生成的结构图,编写m文件的解释:
sec = 2; % 定义级数
SOS = [1 0 -1 1 -1.9941159332576488 0.99413480892694572;1 0 -1 1 -1.8630805194585167 0.87259004111123051];G = [0.048551094455762382 0.048551094455762382 1];w = zeros(sec,3); %中间w 变量 ym = zeros(1,sec+1); %每一级的输出for i = 1:len % 对每一个输入 x ym(1) = x(i); for k = 1:sec % 分极计算 w(k,1) = ym(k) * G(k) - w(k,2) * SOS(k,5) - w(k,3) * SOS(k,6) ym(k+1) = w(k,1)*SOS(k,1)+w(k,2)*SOS(k,2)+w(k,3)*SOS(k,3); w(k,3) = w(k,2); w(k,2) = w(k,1); end y(i) = ym(sec+1)*G(sec+1); %得到输出end翻译成C语言// 20-500hz butterworth 4 order 2 section 3750sps#define SEC 2const float SOS1[SEC][6] = {{1, 0, -1, 1, -1.9528158412163148, 0.95399450820943588}, {1, 0, -1, 1, -0.92310027138083539, 0.34076352170725532}}; const float G1[SEC+1] = {0.31856548677578983,0.31856548677578983,1}; float BandPassFilter(const float SOS[SEC][6],const float G[SEC+1],float x){ static float w[SEC][6]; uint8_t k; static float ym[SEC+1]; ym[0] = x; for(k = 0;k < SEC;k++){ w[k][0] = ym[k] * G[k] - w[k][1]*SOS[k][4] - w[k][2]*SOS[k][5]; ym[k+1] = w[k][0]*SOS[k][0]+w[k][1]*SOS[k][1]+w[k][2]*SOS[k][2]; w[k][2] = w[k][1]; w[k][1] = w[k][0]; } return ym[SEC]*G[SEC];}复制代码每采集到一个数据时,以输入数据作为参数,调用BandPassFilter(),得到一个滤波输出。相当于实时处理。
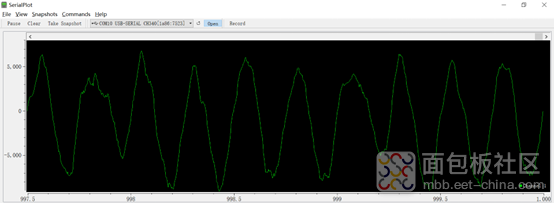
经过滤波后的信号
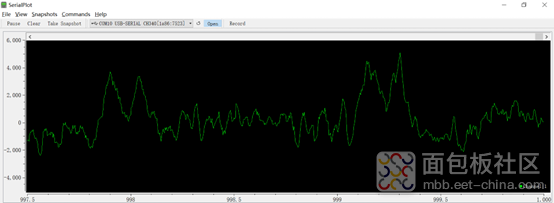
经过滤波+陷波后的信号










 /5
/5 
文章评论(0条评论)
登录后参与讨论