原创 MATLAB信号处理仿真-使用函数封装，多音正弦和谱分析

在 “正弦信号的DFT分析”一文中，我们使用了kaiser窗和FFT进行谱分析多音正弦信号，在数字信号处理的领域，两个主要的话题就是信号的分析与合成。所以，我们会非常频繁的使用到多音正弦信号以及加窗的频谱分析。

matlab是一种脚本式的编程语言，从某种意义上说也是计算机学科的一部分，在软件行业里面，重用是非常重要的思想，把经常要重用的代码用函数（面向过程）或是类（面向对象）封装起来，留出接口的数据类型定义，以后就可以很方便的再次用到。

对于多音信号，我们在生成这种信号时，会有不同的需求，比如信号的采样率是多少；信号里面有几个频率成分，分别是多少；信号的向量长度是多少；以及信号的量化精度是多少。嗯，对于数字信号处理的新手同学们，请一定要时刻想着离散信号的采样率和量化精度。只有配备了这些参数，一个离散序列才真正的被赋予了“数字信号”的意义。由于这些信号配置参数需要在生成信号的时候指定，所以，把这些参数作为生成多音信号函数的入口参数。

同样，对于谱分析函数，需要配置输入信号的采样率，如果把输入信号作为一个单帧的向量，分析长度通常是选取距离这个向量最近的2的N次方的数值，比如输入数据150点则选择分析长度为128，这是因为matlab的基2-FFT的算法最快，其他的特殊点数算法比较慢。另外，由于待分析信号的频率成分未知，就是说我们不知道里面可能有几个谱峰以及它们的距离远近，所以，窗函数的形状需要可以动态指定，所以说凯泽窗是个非常有用的东西，因为它把窗函数的形状给数值化了，我们不用再记录一堆繁琐的窗函数的名字了。

接下来就是把之前的正弦分析代码重用的例子，我们封装了两个函数，一个是生成多音正弦的函数，一个是对输入数据进行频谱分析的函数，顶层代码可以是函数或是命令脚本。

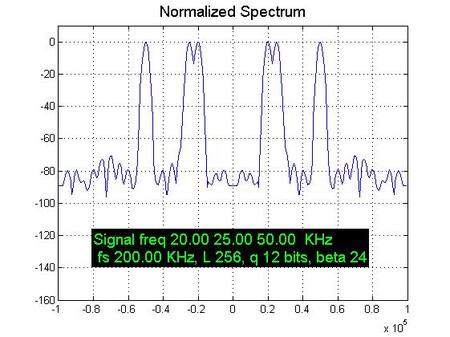
然后，我们看张图片轻松一下，在频率成分较多的情况下，12比特的量化噪声毛刺已经突破了-80dB大关了（-80dB是某些通信设备的一个规格门限），对于观察噪声这事情吧，通常咱们看频域，因为时域里面实在是充满了伪装。

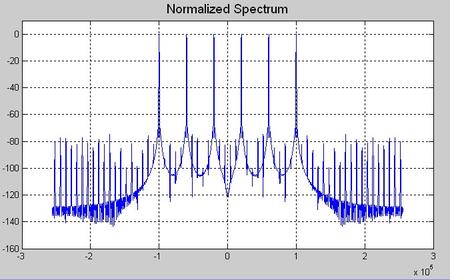
OK，既然我们用函数来封装了代码，那么主程序里面的代码变得简洁，这样有利用我们来折腾，所谓仿真的意义就是，在实际动手之前把各种情况都看看，对于我们这个多音正弦的谱分析，我们可以调节的是分析长度（即fft的样点数）和窗函数的形状，另外采样率也可以调节，不过一般硬件系统中，不会很随意的调整AD变换器的工作频率，通常ADC都是工作在设定好的具有最佳噪声表现的时钟频率上。

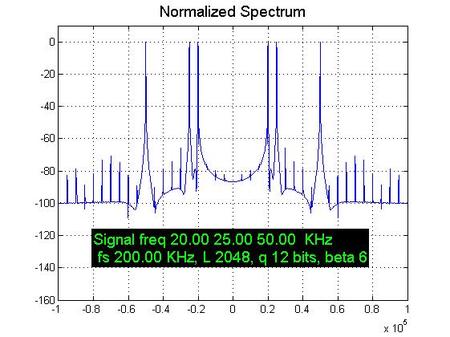
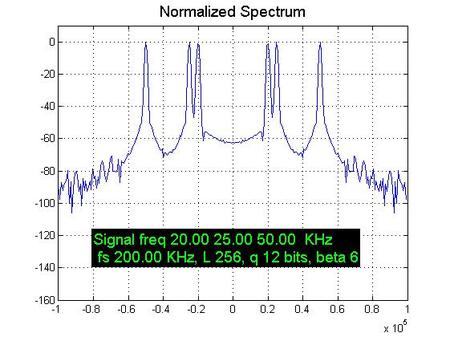
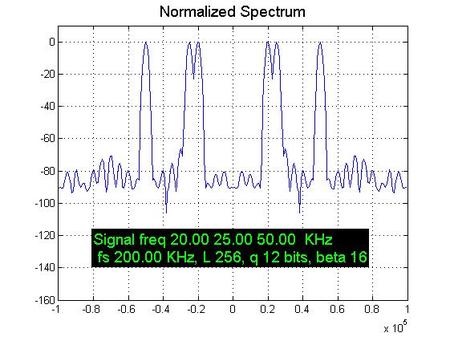
好了，我们开始看系列图片吧，为了让图片中能够记录配置参数，在代码里面调用了打印文本的函数。

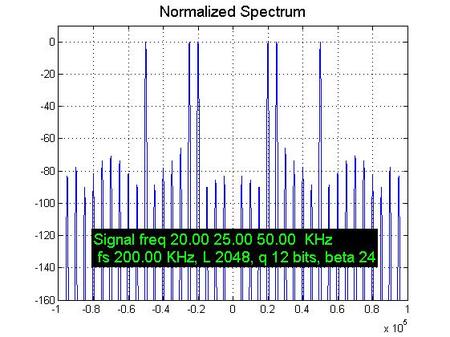
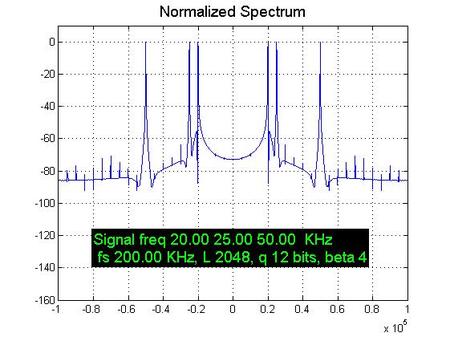
嗯，接下来呢，如果您是要学习数字信号处理的本科生，那么我强烈建议您尝试修改这个仿真里面的参数，亲自观察一下类似的效果，同时，俺也非常衷心的希望你能在调节这些仿真参数的时候明白“时域和频域的互相测不准”的道理，即：为了提高频域的物理分辨率，唯一的方法就是提高记录时间长度，其他的都无效。

我非常有信心，若您考取了信号处理或是通信类研究生，在之后的科研工作中，会遇到类似的问题，俺之所以不厌其烦的上传这么多频谱图片，因为这个的确是信号处理领域里面一个太基础而重要的话题，无论是探测隐身飞机，还是从电视画面中学习总书记同志的重要讲话，以及用wifi从互联网上面翻墙看个视频啥的，底层的信号链路通通要用到类似的过程。

所有这些，可以总结为以下的问题，如果有两个频率的正弦信号，f1和f2，它们的幅度分别是A1和A2，如果我们用频率fs对它们进行采样，记录的长度是L，用beta阶的凯泽窗进行加窗后做DFT分析，在这样的假定下，我们应当如何调节fs，L和beta，使得我们能够在DFT的结果里面区分出这两个频率的谱线，尤其是在两个信号频率很接近，幅度又差别很大，我们要探测那个幅度较小的信号的存在是最困难的。为什么说是探测出存在，而不是测量出数值呢，因为“有和无”是比“多与少”更重要的话题，“有和无”决定了无线路由器是否开启，频率上是否有广播节目，以及. . . . . .敌人的飞弹是否来袭。

（注：为了简洁，我们的仿真代码没有考虑正弦信号幅度的问题，但是这也是个重要因素）

。