原创 MATLAB信号处理仿真-正弦信号的DFT分析

每年夏天，开学前后，便会带领大三的小朋友一起做一些正弦信号谱分析的实验， 作为给他们信号处理的上手训练。
大致的内容就是，先用Verilog做个DDS的数字电路下载到FPGA里面，然后用SignalTap把FPGA板子上的运行的数据抠出来，使用文本编辑器的列操作功能改改格式，然后导入的matlab里面分析一下频谱。
一旦要分析频谱，那些在数字信号处理课程上恼人的问题就又来了，补零，加窗，分析分辨率，物理分辨率，等等。

另外，这种实验课执行起来，发现三年级的学生对于matlab的语法实在是头疼，于是干脆写一个参考的代码给大家用来做为修改的起点吧

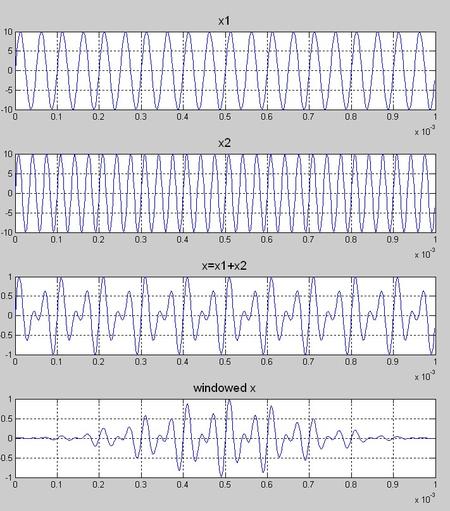
该仿真的用途在于，配置信号的幅频特征参数以及分析参数，然后观察两正弦信号合成后信号的加窗幅度谱。

两正弦波的幅度、频率
信号的量化比特数（通常为8-16）
信号采样率
凯泽窗的beta值，注意，beta=0时，等价位矩形窗，beta越大，主瓣越宽，旁瓣越低。
信号的采样长度，亦即DFT谱分析的长度

通过修改这些仿真参数，可以尝试

在什么情况下，两个正弦的谱峰就重合成一个谱峰，不易分辨了呢？
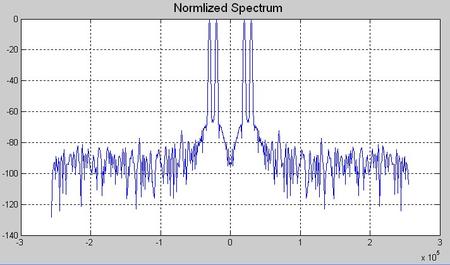
如果两个信号的频率比较接近，但是又不知道具体的频率，只是知道大致的范围，如何调节其他参数（频率和幅度之外的参数），使得有助于分辨出两个正弦信号的谱峰。下面是在某个配置下的仿真输出参数图。

另外，基于上面的实验，请再尝试，在信号的后面补零，提高DFT的分析长度，对于区分不同的谱峰是否有帮助呢。如果你需要进一步了解DFT对于谱分析的应用，请自行搜索“基于DFT的谱分析”。

对于matlab新手的一点点补充
1、尽量使用列向量，matlab内部是向量按列存放。
2、a = [1;2;3;4]定义一个列向量，中括号用于拼接标量为向量，也可以拼接向量为更大的向量，但是注意被拼接的应当都是行向量或都是列向量
3、b = a(1:3) 把向量a的1号到3号分量取出，保存到b向量，圆括号用于进行分量寻址，冒号用于指定范围，1:3 这个表达式生成了一个行向量，[1 2 3]，这个行向量被作为寻址的参数给a向量取出分量。
4、共轭转置和普通转置，a  = [1+j, 2+j, 3+j] ;  b = a'; c=a.'; b是a的共轭转置，c是a的普通转置。这两个转置的混淆会导致非常隐蔽的错误。

贴一下代码吧