原创 c语言延时函数

 2008-12-26 10:17  6491 10 12 分类: MCU/ 嵌入式

参考了51单片机 Keil C 延时程序的简单研究，自己也亲身测试和计算了一些已有的延时函数。

这里假定单片机是时钟频率为12MHz，则一个机器周期为：1us.
参考了51单片机 Keil C 延时程序的简单研究后，我们可知道，在Keil C中获得最为准确的延时函数将是

void delay(unsigned char t)

{

while(--t);

}

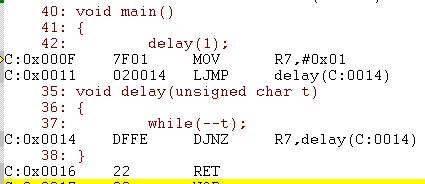
反汇编代码如下：

执行DJNZ指令需要2个机器周期，RET指令同样需要2个机器周期，根据输入t，在不计算调用delay()所需时间的情况下，具体时间延时如下：

t	Delay Time (us)
1	2×1+2 ＝4
2	2×2＋2＝6
N	2×N＋2＝2(N＋1)

当在main函数中调用delay(1)时，进行反汇编如下：

调用delay()时，多执行了两条指令，其中MOV R, #data需要1个机器周期，LJMP需要2个机器周期，即调用delay()需要3us.

Keil C仿真截图与计算过程:

加上调用时间，准确的计算时间延时与Keil C仿真对比如下：(可见,仿真结果和计算结果是很接近的)

t	Delay Time (us)	仿真11.0592Mhz时钟(us)
1	3＋2×1+2 ＝7 \| 7.7(实际)	7.60
2	3＋2×2＋2＝9 \| 9.9	9.76
N	3＋2×N＋2＝2N＋5 \| (2N+5)*1.1	/
3	11 \| 12.1	11.94
15	35 \| 38.5	37.98
100	205 \| 225.5	222.44
255	515 \| 566.5	558.81

也就是说，这个延时函数的精度为2us，最小的时间延时为7us，最大的时间延时为3+255×2＋2＝515us.
实际中使用11.0592MHz的时钟，这个延时函数的精度将为2.2us，最小时间延时为7.7us, 最大时间延时为566.5us.
这个时间延时函数，对于与DS18B20进行单总线通信，已经足够准确了。

现在，我们将时钟换成11.0592MHz这个实际用到的频率，每个机器周期约为1.1us.
现在让我们来分析一下这个之前用过的延时函数：

//延时函数, 对于11.0592MHz时钟, 例i=10,则大概延时10ms.

void delayMs(unsigned int i)

{

unsigned int j;

while(i--)

{

for(j = 0; j < 125; j++);

}

它的反汇编代码如下：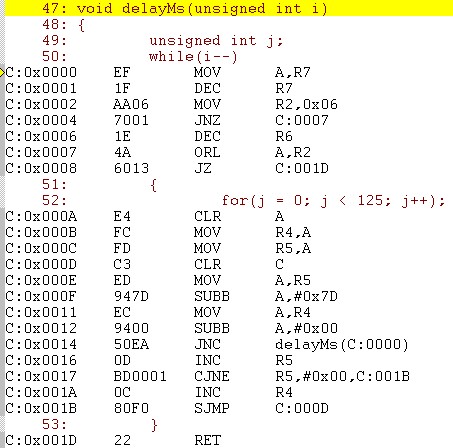

分析: T表示一个机器周期(调用时间相对于这个ms级的延时来说，可忽略不计)

1  C:0000      MOV   A,    R7       ;1T
2                   DEC   R7                ;1T   低8位字节减1
3                   MOV   R2,   0x06   ;2T
4                   JNZ   C:0007          ;2T   若低8位字节不为0, 则跳到C:0007
5                   DEC   R6                ;1T   低8位字节为0, 则高8位字节减1
6 C:0007      ORL   A,   R2         ;1T
7                   JZ      C:001D         ;2T   若高8位也减为0, 则RET
8                   CLR   A                  ;1T   A清零
9                   MOV   R4,   A        ;1T   R4放高位
10                   MOV   R5,   A        ;1T   R5放低位
11 C:000D      CLR   C                  ;1T   C清零
12                   MOV   A,   R5        ;1T
13                   SUBB   A, #0x7d    ;1T   A = A-125
14                   MOV   A,   R4        ;1T
15                   SUBB   A,  #0x00   ;1T   A
16                   JNC  C:0000           ;2T   A为零则跳到C:0000
17                   INC   R5                 ;1T   R5增1
18                   CJNE R5,#0x00, C:001B ;2T   R5>0, 跳转到C:000D
19                   INC   R4                 ;1T
20 C:001B      SJMP      C:000D    ;2T
21 C:001D      RET

对于delayMs(1), 执行到第7行就跳到21行, 共需时12T, 即13.2us
对于delayMs(2), 需时9T＋13T＋124×10T＋7T＋12T ＝ 9T＋13T＋1240T＋7T＋12T ＝1281T ＝1409.1us.
对于delayMs(3), 需时9T×(3-1)＋(13T＋124×10T＋7T)×(3-1)＋12T
＝1269T×(3-1)＋12T＝2550T＝2805us.
对于delayMs(N),N>1, 需时1269T×(N－1)＋12T = 1269NT－1257T＝(1395.9N-1382.7)us.

利用Keil C仿真delayMs(1) = 0.00166558s = 1.67ms 截图如下: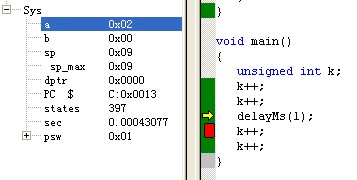

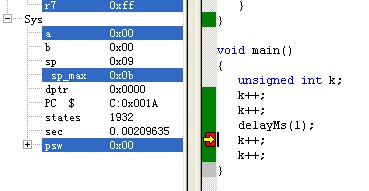
由分析可知具体的计算延时时间与Keil C仿真延时对比如下：

i	Time Delay	仿真延时
1	13.2us	1.67ms
2	1409.1us	3.31ms
3	2805us	4.96ms
N	(1395.9N－1382.7)us
10	12.6ms	16.50ms
20	26.5ms	32.98ms
30	40.5ms	49.46ms
50	68.4ms	82.43ms
100	138.2ms	164.84ms
200	277.8ms	329.56ms
500	696.6ms	824.13ms
1000	1394.5ms	1648.54ms
1500	2092.5ms	2472.34ms
2000	2790.4ms	3296.47ms
5	5.6ms	8.26ms
73	100.5ms	120.34ms
720	1003.7ms = 1s	1186.74ms