Booth乘法器设计
booth乘法器是一种可以计算带符号数的乘法器,他的实现思维较为简单,具体的重要逻辑是设乘数分别为a[3:0]和b[3:0],积为y[8:1],在这里y其实是一个9位的寄存器,只不过高8位才是真正的结果。首先我们把b[3:0]装进y[4:0]的高四位,低一位装一个1'b0,之后我们便可以实现我们的逻辑了判断y[1:0],如果为2'b00或者2'b11,则不操作,如果为2'b01,y[8:5]+a,如果为2'b10,则y[8:5]-a;之后再判断y[8],如果为1'b1则右移一位,再把y[8]置1,如果为1'b0则有一位,再把y[8]置0,重复以上步骤4次,最后就会得到积为y[8:1]。
在这个给出代码
- module booth(clk,rst_n,a,b,y,start,done);
- input clk,rst_n;
- input [7:0]a,b;//输入乘数a,b,8位
- input start;//开始信号,只有在高电平时,乘法器才工作
- output [15:0]y;//积,为16位
- output done;//完成一次乘法信号会输出一个高电平
-
- reg[16:0]y_reg;//17位的寄存器,用来完成移位和加法的操作
- reg[4:0]i;//状态寄存器
- reg done;
- reg [7:0]temp1,temp2;//中间变量,用来简化移位操作
-
- always @ (posedge clk or negedge rst_n)
- begin
- if (!rst_n)
- begin
- y_reg<=17'd0;
- i<=4'd0;
- done<=1'b0;
- temp1<=8'd0;
- temp2<=8'd0;
- end
- else if(start)
- case(i)
- 0:begin
- y_reg<={8'd0,b[7:0],1'b0};
- i<=i+1'b1;
- temp1<=8'd0;
- temp2<=8'd0;
- end
- 1,2,3,4,5,6,7,8:begin
- temp1=y_reg[16:9]+a;
- temp2=y_reg[16:9]-a;
- if(y_reg[1:0]==2'b01)
- y_reg<={temp1[7],temp1,y_reg[8:1]};
- else if(y_reg[1:0]==2'b10)
- y_reg<={temp2[7],temp2,y_reg[8:1]};
- else
- y_reg<={y_reg[16],y_reg[16:1]};
- i<=i+4'd1;
- end
- 9:begin
- done<=1'b1;
- i<=i+4'd1;
- end
- 10:begin
- done<=1'b0;
- i<=4'd0;
- end
- endcase
- end
- assign y=y_reg[16:1];
- endmodule
重点分析booth算法中最重要的逻辑
- 1,2,3,4,5,6,7,8:begin
- temp1=y_reg[16:9]+a;
- temp2=y_reg[16:9]-a;
- if(y_reg[1:0]==2'b01)
- y_reg<={temp1[7],temp1,y_reg[8:1]};
- else if(y_reg[1:0]==2'b10)
- y_reg<={temp2[7],temp2,y_reg[8:1]};
- else
- y_reg<={y_reg[16],y_reg[16:1]};
- i<=i+4'd1;
- end
在这里的8个循环中,我们再一个步骤里完成了判断和移位的两个操作,我们先用了两个变量,temp1,temp2,来计算y_reg[16:9]+a和
y_reg[16:9]-a的值,那么在下一步的判断中,就可以直接完成移位的操作了,大大缩短了时钟的周期。在这里贴一个在网上找到的流程图,就知道booth乘法器是怎么样工作的了。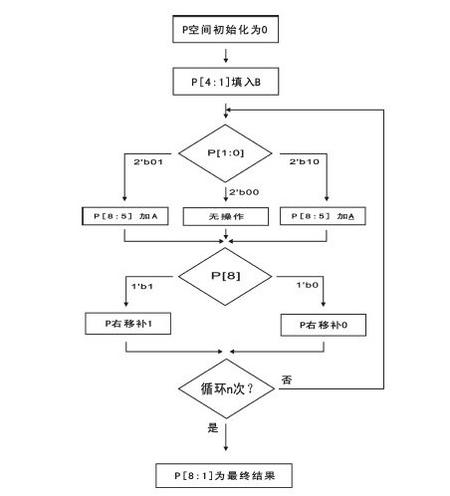
我们来分析一下booth算法中的数学原理是怎么样的,在网上查找了很多资料,都只直接给出了流程图,或者是计算的步骤,并没有说出到底为什么这样可以成立,当中蕴含着的数学原理是什么,我们来探讨一下。
因为有些符号不知道怎么打出来,我直接用了草稿纸写了推导过程。



 /1
/1 
用户1696769 2015-11-5 17:19