原创 由简单的加法器揭秘FPGA底层实现

近日在用QuartusII做时序仿真的时候突然发现了一个奇妙的事情，仔细研究后发现FPGA电路的实现原来还有一定的奥秘。

首先，用verilog在QuartusII上做了个简单的两8bit有符号输入、一路9bit有符号输出的加法器。代码如下：

需要注意的是：只有当输入输出数据都是signed类型，或者说加法运算的加数与被加数都是signed类型时，“+”加法运算才算是有符号加法。简单介绍下有符号加法的运算，以4bit为例，如：

1111 + 0011 = 10010 ——直接的二进制加法

1111 + 0011 = 0010 ——4bit的补码运算，对应的十进制数相加：

-1 + 3 = 2

有符号加法：

数值相加：1111 + 0011 = 10010

符号位相加：1+0=1

符号位运算：1+1=0

结果输出：1111 + 0011 = 00010

做好这个简单的有符号加法器之后，便直接用QuartusII自带的仿真器对其进行仿真：

仿真数据我们也不需要做的太复杂，固定加数1为1，加数2自加。

好的，这个时候我们看到上图中OUT的输出大体数据都是正确的，但在两个数中间有些毛刺！大多数人都认为这是竞争与冒险，觉得都很正常……的确，这是正常的现象，而且这样的结果并没有错。

我们将毛刺放大后，便会发现其中的奥秘了……

我们可以发现在7和8两个正确结果中间，毛刺的数值是3、1、0。大多数人的第一反应肯定和我一样，认为这是随机的现象，这几个数并没有什么含义。实际则不然！

我们将数值转换成bit形式：

可以惊奇地发现，从7到8的变化过程是这样的0111-0011-0001-0000-1000，这类似于格雷码，是1bit变化的模式！（不仅是7到8的变化，凡是有“毛刺”的地方其实都是这样的变化过程）

我们再将加法器的中间变量仿真出来看看：

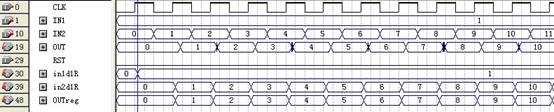
可以看出，当做完加法后的结果OUTreg并没有出现毛刺，而直到OUT输出才出现这样的变化，可见寄存器的最后输出是呈现1bit变化的格雷码形式的。