


运算放大器中有表示特性的代表性参数。
若给放大电路的输入增加电压,则在其输出时,会出现输入电压放大率的倍数。该放大率用输出电压的大小除以输入电压的大小所得的值表示。
若将输入电压表示为Vs 、输出电压表示为Vo 、放大率表示为Av,则可定义如下。
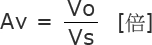
放大率常用对数的20倍用分贝[dB]单位表示。
例如,运算放大器的开放增益为100000倍(105倍)时,可将其用分贝表示如下。

这样,即使是有10的多个次方的庞大放大率,若使用分贝表示,就可表示为较小数值100[dB]。
另外,以下整理了表示模拟电路所需的各种单位。
(a) dB : 2个量之比的对数的10倍或20倍。

(b) Vp-p : 波形的最大值与最小值之差。
(c) Vrms : 有效值 平方均值的平方根。
1Vrms = 2√2
(d) dBV : 以1Vrms为基准的表达式。
0dBV= 1Vrms
(e) dBm : 以对某负载产生1mW的功率的电压为基准。
普通负载的值多为50Ω、600Ω等。
0dBm=0.224Vrms (负荷为50Ω时)
0dBm=0.775Vrms (负荷为600Ω时)
(f) oct : 为"倍频程",1oct表示某频率的2倍的值。
-6dB/oct表示频率为2倍时,降低6dB。
(g) dec : 为"十倍频程",1dec表示某频率的10倍。
-20dB/oct表示频率为10倍时,降低20dB。
※根据(f)、(g)、 -6dB/oct= -20dB/dec。
(h) dB(分贝)计算基础
3dB ≒ 1.41倍 ≒ √2
6dB ≒ 2.00倍
10dB ≒ 3.16倍
20dB ≒ 10倍
ex)16dB=10dB+6dB → 3.16×2=6.32倍
输入偏置电压是指有差分输入电路的运算放大器或比较器带有的误差电压。理想运算放大器或比较器的偏置电压为0V。
给运算放大器或比较器的输入引脚输入同相(相同)电压时,理想运算放大器不会输出偏置电压,但存在输入偏置电压时,就会输出与输入偏置电压相应的输出电压。
将该输出电压控制为0V所需的输入引脚间的电压差被称为输入偏置电压,该值为输入换算值。
作为输入换算表示的优点是,由于运算放大器、比较器可在各种放大率或电路结构中使用,若作为输入换算电压表示,那么就可以轻松地估量其对输出电压的影响。
偏置电压的单位一般表示为[mV]或[µV]。
值越接近0越趋于理想状态。

在同相输入范围外的领域,偏置电压急剧增加,此领域内不再作为运算放大器或比较器进行工作。
另外,对偏置电压的出现频率进行观测,发现其以0V为中心正常分布。 即,在规定范围内随机分布。
通常,规格值的表示以绝对值记载,因此实际上具有+极性和-极性两种偏置电压。
转换速率是表示运算放大器的工作速度的参数。
表示输出电压在规定的单位时间可变化的比例。
例如,1[V/µs]表示在1[µs]内可使电压发生1[V]的波动。
理想运算放大器可忠实地输出任何输入信号对应的输出信号,但实际上还存在一种叫做转换速率的限制。
给输入施加上升沿和下降沿比较陡峭的矩形波脉冲时,表示输出电压在单位时间内可发生什么程度的变化。下图表示转换速率的定义。

上升沿和下降沿的转换速率按下式计算。
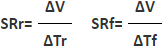
转换速率按"上升沿"或"下降沿"中较慢的一方为基准进行规定。
因此,表示运算放大器输出信号的斜率的最大值。
对于波动更剧烈的信号,输出波形难以跟随而发生变形。构成放大电路时,转换速率是输出变化的比例,因此不会发生变化。
运算放大器用于直流、交流两者的信号放大。
运算放大器受响应速度限制,并非可处理任何信号。
在上图所示的电压跟随器结构中,直流电压输入受到输入电压范围和输出电压范围的限制。
此外,带有频率的交流信号还受到增益带宽积和转换速率的制约。
此处对振幅与频率的关系,即转换速率加以考虑。
求运算放大器可输出的最大频率。

求输出右图所示波形所需的转换速率。
y=Asinωt
转换速率是正弦波的切线的斜率,故对上式进行微分。

转换速率为
SR=Aω ω=2πf
再者,正弦波的振幅是峰间值,VPP=2A,因此,可进行如下变形。
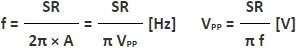
该频率f被叫做全功率带宽。
它们处于运算放大器未设定放大率的状态,即电压跟随器中运算放大器的可输出振幅(在输出电压范围内)与频率的关系。

振幅保持不变且超过上述求得的频率时,波形受转换速率限制,正弦波变为三角波,发生失真。
 /5
/5 
文章评论(0条评论)
登录后参与讨论