原创 米勒平台的形成原理

由此可见，反向电压放大器增加了电路的输入电容，并且放大系数为（1+Av）。这个效应最早是由 John Milton Miller 发现的并发表在他 1920 的著作中，所以称之为米勒效应。

再联系到我们的 MOSFET，加入寄生电容的原理图可以由下左图来表示。假设想象图 2（1）的的 MOSFET 是一个共源电路（common source）：Drain 为输出端，Source 接地，Gate为输入端。根据 MOSFET 的小信号模型，MOSFET 形成了一个反向电压放大器，其等效电路可以由图 2（2）来表示。

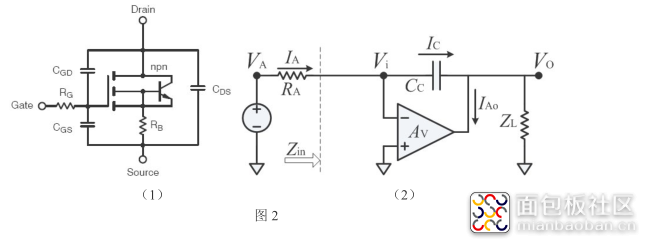
MOSFET 形成的电压放大器的增益需要根据其输出和输入电阻来判断，不同的 MOSFET 会有不同的结构，所以增益很难量化，某些情况下其放大系数可以达到数百倍。CGD 则形成了一条反馈回路（连接输出端口 Drain 和输入端口 Gate），于是在 MOSFET 中的米勒效应就形成了。

接下来就是万众瞩目的米勒平台了，MOSFET 开启时的电压和电流曲线如图 3 所示。

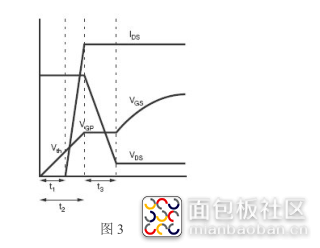
在 0-t1 的时间内上升到 MOSFET 的阈值电压。漏极电流 IDS 从 t1 结束时到 t3 开始时从 0 上升到稳定负载电流，VGS 继续上升到米勒平台电压 VGP。在 t3 时间内，VGS 一直处于平台电压，VDS 开始下降至正向导通电压 VF。在 t3 时间后，VGS 继续上升。这里我们来分析一下为什么波形会是这个样子。

首先，我们需要先要了解一下 MOSFET 寄生电容的大体情况。在 MOSFET 的 DATASHEET中，采用的定义方法如图 4 所示。需要注意的是，Crss 就是我们所说的 CGD。

一般而言，在 MOSFET 关闭的状态下，CGS 比 CGD 要大很多。以大家熟知的 IRF540 为例，

IRF540 的 Ciss=CGS+CGD=1700pF, Crss=CGD=120PF, 那么 CGS=Ciss-CGD=1580pF. 需要指出的是两者的值都与电容两端的电压相关，这也就是为什么在 DATASHEET 中会标明测试的条件。因此，相应的瞬态电容值与乘积（CGS*VGS）和（CGD*VGD）的斜率有关。

接合 MOSFET 的图 3 来看，在 t3 时间之前，由于 CGS 远大于 CGD，所以在此时间段内 VGS的上升斜率主要有 CGS 决定。当 t3 开始时，参照式（2，）VGD 的变化使得给 CGD 在这个时间段内的电容值增加，同样使得充电电流迅速增加。所以在 t3 时间内，VGS 的斜率主要由 CGD的来决定。值得注意的是，VGS 在 t3 阶段内的斜率往往都很小甚至为 0，这是因为 VGD 在这段时间的电压变化非常大，使得门极中的大部分电流都用来给 CGD 充电，从而只有很少或者没有电流流向 CGS。再次使用 IRF540 为例，在DATASHEET 上的有这么一组数据，Qgs=11nC,Qgd=32nC. 从前面可以看出，MOSFET 关断状态下的 CGD 远远小于 CGS，但是却需要更多的充电电荷。仔细看 Qgd 的注释中，标明了是受到了“Miller”米勒效果的放大。

在 t3 时间段以后，VGD=VF 且不再变化，此时的 CGD 的电容值也就变成了一个固定的值，并且容值比之前大了很多甚至接近于 CGS。因此，在 t3 之后的 VGS 上升的斜率不如在 t1 内的那般陡峭，而是平缓了很多如图 3 所示。

很多人在测试 VGS 波形的时候，观测到的并不是一个平台，而是一个坑，既在平台之前有一个电压尖峰。