原创如何评估采样系统时钟要求（一）之抖动对ADC信噪比（SNR）的影响 ...

 2019-7-21 22:01  11682 48 5 分类: 测试测量文集: 系统方案

简介

在ADC应用中，最常见的一个问题是如何提供编码源。若要使所选数据转换器实现最佳性能，正确选择编码时钟至关重要。随着近年来采样模拟输入频率不断增高，这一点显得尤为重要，那么时钟抖动对采样系统影响有多大、如何量化，本文是“如何评估采样系统时钟要求”第一部分，主要描述抖动抖动对ADC信噪比（SNR）的影响。

1. 采样保持放大器基本概念

探究ADC输入端时，无论ADC电路形式如何，总是离不开采样保持放大器构架（SHA），如图1.1所示，SHA由四个主要部分组件，输入放大器（input amplifier）、储能装置(capacitor)、输出缓冲器（output buffe）和开关电路（switchingcircuits）对于所有的SHA电路都是通用的。

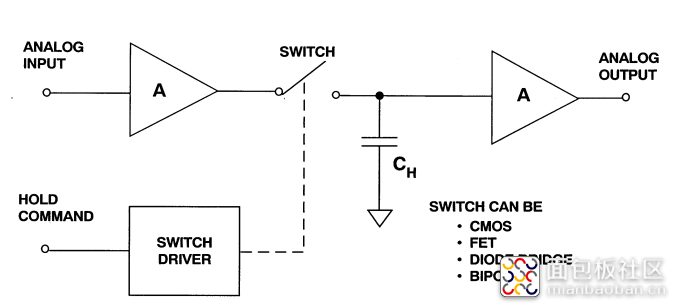
图1.1 采样保持放大器基本构架

保持电容作为SHA的核心，输入放大器提供信号源提供高阻抗转换并且提供了提供电流增益来驱动采样电容，如图1.2所示，在采样模式下，开关闭合，电容两端电压跟随输入信号进行变化，同时具有输入信号相同延时和带宽限制。在保持模式下，开关断开，电容保持在与输入缓冲器断开连接之前的电压，同时输出缓冲器为保持电容器提供高阻抗，以防止保持电压泄露而出，基本的SHA转换过程，主要分为四种，跟踪模式（track mode）、跟踪转保持模式（track-to-hold transition）、保持模式（hold mode）、保持转跟踪模式（hold-to-track transition），本文主要涉及的内容在track-to-hold transition下，其他模式就不详细描述了，因为在track-to-hold transition下参数变化直接影响采样系统的性能。

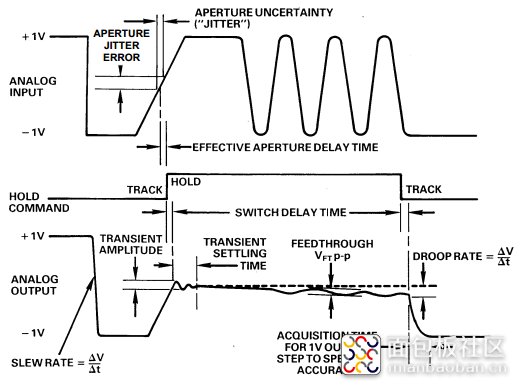
图1.2采样保持时域的波形变化

1.1孔径时间（Aperture Time）

在track-to-hold transition模式下，误解最深、滥用最多的可能是那些包含“孔径” 的一些参数，如图2.1给出了一个简单的模型，SHA最基本的动态特性是它能够快速断开保持电容与输入缓冲放大器的连接，这一动作所需的极短（但非零）时间间隔称为“孔径时间”（或“采样孔径” ）ta，此间隔结束时电压保持的实际值取决于输入信号压摆率和开关操作本身引入的误差。图2.1显示对两个任意斜率的输入信号（分别标为1和2）应用保持命令时的情况。为清楚起见采样保持基底误差和开关瞬态忽略不计。最终保持的值是输入信号的延迟版本，并且是开关孔径时间范围内的平均值。该一阶模型假设，保持电容上的最终电压值约等于应用于开关的信号在开关从低阻抗变为高阻抗的时间间隔(ta)内的平均值。即可以理解为开关变换的过程，由低阻抗到高阻抗实际等效为一个平均阻抗的变换，实际上切换的过程是不线性的。

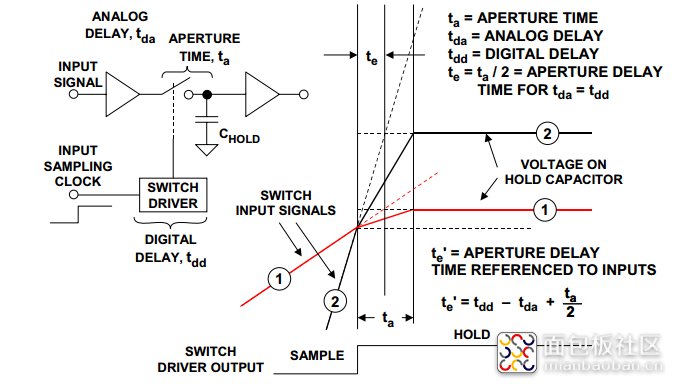
图2.1采样保持波形和定义

1.2孔径抖动（Aperture Jitter）

但是如果采样时钟中存在样本间变化，则会产生相应的电压误差，如图2.2所示。在开关断开的时刻，这种样本间变化的不确定性我们成为“孔径抖动” ，通常用均方根皮秒(ps rms)来衡量。

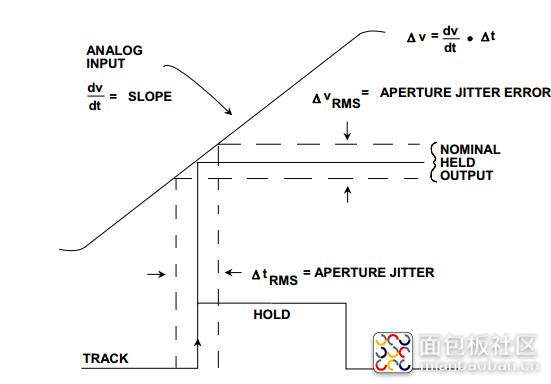
图2.2孔径抖动

通过下面的简单分析，可以预测抖动对理想ADC SNR的影响。假设输入信号由下式给出为：V（t）=Vo sin（2πf*t）

对输入信号微分，求出信号的变化速率为：dv/dt=2πf×Vo cos（2πf*t）

同时将幅度2πfVo除以√2可以获得dv/dt的均方根值：dv/dt|rms=(2πf*V0)/√2

令∆V_rms均方根电压误差，Δt 为均方根孔径抖动tj，那么上式变换为：∆V_rms=(2πf*V0* tj)/√2

2采样系统以及时钟相位噪声和抖动的影响

2.1抖动对ADC信噪比(SNR)的影响

从∆V_rms均方根电压误差来看，采集后电压值得误差随输入频率线性增加，所以在高频段，比如中频采集接收器应用中，时钟参数指标变得非常重要。其实对于采集系统，采集的过程我们可以理解为一个混频过程，输入信号乘以本振，才采样系统中这个本振就是ADC的采样时钟。因为时域上乘法在频域上是卷积，所以采样时钟的频谱和输入信号的频谱卷积就是ADC采样的结果，也就就是就说时钟的频谱会进入ADC采样的结果中，采样之后的时钟抖动就会显现为带宽噪声在采样频率周围周期性的重复。

时钟输入噪声和ADC自身抖动的影响可以扩展至采样速率的很多倍并混叠到转换器的基带上，因此这个带宽噪声会降低ADC的底噪性能。假设满量程输入正弦波的均方根值为VO/√2，因此均方根信号与均方根噪声的比值（用dB表示）为：

相应输出误差的幅度与模拟输入的变化速率有关。针对既定的孔径抖动值，孔径抖动误差随着输入dv/dt提高而提高。相位抖动对外部采样时钟（或模拟输入）的影响也是产生同样类型的误差。因此，tj总抖动量为外部采样时钟抖动与ADC孔径抖动的方和根。该公式假设ADC具有无限的分辨率，孔径抖动是决定SNR的唯一因素，它说明孔径和采样时钟抖动对SNR和ENOB有严重影响，特别是当输入/输出频率较高时。从上式足以看出一个稳定的、低抖动的时钟源对ADC是多么的重要。比如考虑ADC抖动和时钟抖动后，我们有一个300fs的均方根时钟抖动的采样时钟，对于200MHz模拟输入信号而言，根据上式SNR限制为68.5dB，也就是有效位被限制在11.08bit，也就是ADC理想的最优指标，但是没有考虑ADC模拟链路上P/N相位和幅度不平衡、电源噪声、ADC自身参数等带来的误差。

如果忽略掉ADC模拟链路上P/N相位和幅度不平衡、电源噪声的影响，将ADC自身参数考虑进来，那么时钟抖动和ADC孔径抖动，并不是不完全是性能的制约因素，如果考虑ADC的微分非线性（DNL）参数和热噪声的影响，那么上面的等式会变得更加有趣，也就是增加量化噪声项，公式增加为如下：

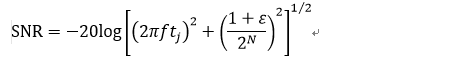
其中：

F为模拟输入频率

Tj为总抖动量为外部采样时钟抖动与ADC孔径抖动的方和根

ε最低有效位的“复合均方根DNL”噪声，包括热噪声

N为位数

这个公式为数据转换器的噪声性能提供了计算和量化的过程

2.2利用FFT技术测量ADC抖动

有了增加了ADC的微分非线性（DNL）参数和热噪声及总抖动，SNR量化公式，用于测量ADC SNR、SFDR等参数的FFT测试程序提供了一种出色的孔径抖动间接测量方法需要注意的是，测量结果不仅包括ADC内部孔径抖动，而且包括采样时钟发生器的抖动。因此，所选发生器的均方根抖动规格应当比待测ADC的额定孔径抖动低好几倍（各抖动分量以方和根形式合并），图2.3显示了孔径抖动测试的基本测试设置。

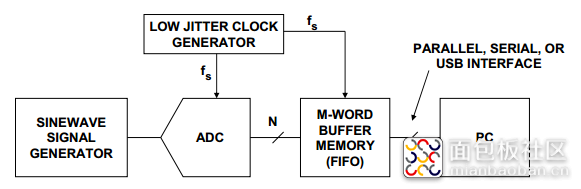
需要进行两次SNR测量，两次测量分别使用频率为fL和fH的满量程输入正弦波。第一次测量是在相对较低的频率fL下测量SNRL，此时噪声主要由ADC等效输入噪声和量化噪声组成。即使对该低输入频率做出些许改变，仍应测量到相同的SNR值。该采样频率一般设置为容许的最大频率。第二次测量是在高输入频率fH下进行SNRH测量，此时孔径抖动对ADC SNR的影响变得明显。根据ADC不同，此频率最高可以达到fs/2。根据计算信噪比计算公式：

SNRL计算为：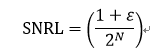

SNRH计算为：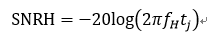

整理两式计算出ADC的总抖动量tj为：

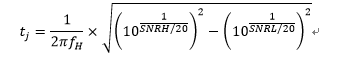
该测试所需的所有测量均使用SNR而不是SINAD（信纳比）。根据FFT输出计算SNR时，必须消除二次至六次谐波（以及直流成分），这一点非常重要，否则将无法获得准确的孔径抖动大小。最后需要说明的是，由于输入信号或ADC采样时钟可能会发生不良抖动，而且布局布线也可能引起抖动和噪声，因此测量小于10 ps rms的均方根孔径抖动异常困难。要获得如此高的精度，频率合成器的抖动必须非常低，此外还应谨慎处理布局布线、信号路由、接地和去耦。