原创 第二章 元件的非理想效应

运用集总参数电路模型来描述和分析电路，使得计算大大简化。集总参数模型通常将电路等效为R，L，C构成的电路。这一章研究RLC的特性，后面再学习传输线的内容打下基础。通过分析，我们会发现，一个在低频时工作良好的电路在高频时对信号产生了畸变，从而有可能使设计的电路无法正常工作。在低频时的分离元件---电阻，电容和电感在高频时表现出截然不同的特性，导线也表现出不同的特性；在低频时可以被忽略的某些现象，如器件的引脚上的电感电容和电阻，在高频时都要成为考虑的对象。

1.电阻

电阻有三种基本的组成形态：（1）碳纤维复合式（2）线绕电阻（3）薄膜电阻。线绕电阻精度最高，碳纤维最差。

1.1电阻的计算

电阻的计算公式在中学时就已经学习过了，这里我们重新拿出来，方便以后使用。

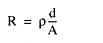
A=横截面积=t x w。

横截面积越小，电阻越大。当高频电流流过导线的时候，电流主要分布在导体表面（这称为趋肤效应），因此，横截面积变小，电阻增大。

1.2 Sheet Resistance的概念

考虑一个很薄的导体，比如PCB上的走线

电阻R=pxd/tw=(p/t)(d/w)=(p/t)n。

当d=w时，n=1，导体变成一个正方形，这时，R=p/t叫做sheet Resistance(表面电阻或方块电阻)。

The sheet resistance will depend on the bulk resistivity of the conductor and the thickness of the sheet。

在PCB制造中，导线的厚度一般使用ounce铜来表示。如1oz(1.4mil)或1/2oz(0.7mil),表示把1oz或1/2oz铜铺在1in²的面积上形成的厚度。

从图中也可以看出，横截面积越小，电阻越大。

[7]介绍了电阻矩阵的内容，仿真软件依据此进行计算。

1.3 趋麸效应[7]

        当导体中的电流频率增加的时候，电流不是均匀的分布在整个导体中，而是趋向分布于导体的表面薄薄的一层，这种现象称为趋麸效应。这一层的厚度叫做趋麸深度。

    但并不是所有电流在趋麸深度处有一个突然的截至，在一个趋麸深度的位置，场强为表面的37%，需要4～5个趋麸深度，场强才能衰减为1%。另外，趋麸效应和温度也有关系。

    由于趋麸效应的影响，相当于导体的横截面积减小，因此，高频时，电阻增大！

趋麸深度的公式和效果如下图所示：

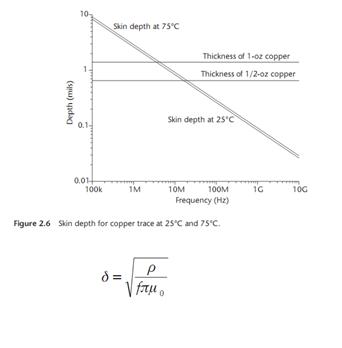
1.4 电阻的非理想效应

    从前面的讨论我们就能知道一点，在频率升高的情况下，电阻可能发生变化。除此之外，还有其他的影响吗？

    从欧姆定律可以知道，理想电阻对所有频率的响应幅值都相等，相位角均为0。实际情况并不是这样。

电阻建模

    实际中的电阻除了标称的阻值之外，还有寄生电容，引线电感的因素存在。以线绕电阻为例，除了电阻之外，还有导线缠绕构成的电容，以及导线自身的电感。对于一个0.5in,引线间隔为0.25in的回路，（线宽16mil），回路的引线电感为14nH，寄生电容为1.2pF，Pspice电路如下。

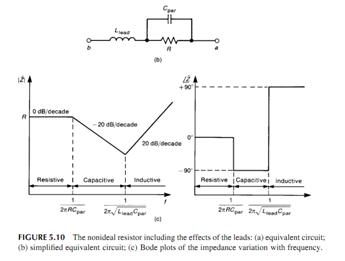
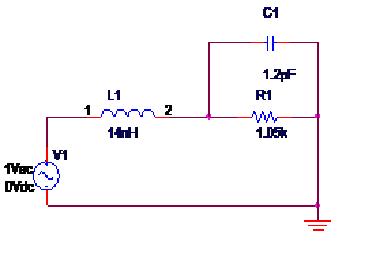
仿真从F=1MHz开始，到10000MHz结束，仿真结果如下。可以看到网络的阻抗变化。

注：由于仿真的结果上传之后十分不清楚，这里就不显示图片了。我上传了一个.doc的word文档（名字是：simulation result of resistor），里面包含了这个电路的原理图和仿真结果。方便各位参考。无法下载的朋友可以发邮件向我要。

    一开始，电阻表现出纯阻性，1Hz----10MHz，阻抗保持不变，1.05K；随着频率的提高，电路表现出容性，并在1.2G左右电感和电容发生谐振，阻抗近乎为0；频率继续提高，电路表现出感性，阻抗急剧增大；随着频率接近无限，电感趋近于开路，阻抗趋近于无穷大。

1.5 电阻的进一步讨论

电阻对频率有一定的依赖性。在高频时，由于趋肤效应，电阻会增加。趋肤效应的讨论可以参考[1]、[3]。

总结：电阻阻抗的这种特性，使得电阻在高频环境下不再表现出电阻的特性，而是表现成为电感的特性，阻抗随着频率的升高和增大。