原创 频率和高速设计_4

7. 集总参数模型

        为了能够获得系统的数学模型，需要知道在什么情况下应用什么样的数学手段来建模。如果系统的模型可以用kirhoff定律而不必使用麦克斯韦方程组的话，建模和计算都可以变得简单。那么，在什么条件下，我们可以用基尔霍夫定律来处理互联的模型呢？

从传输线开始[1]

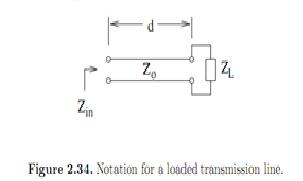
如图，负载阻抗为ZL，传输线阻抗为Z0，传输线的长度是d，输入阻抗是Zin。

结论：输入阻抗Zin=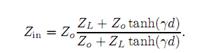

其中，Gama是传播常数=sqrt[(R+jwL)(G+jwC)]。这个公式有两个未知量，Z0和gama。

如果负载短路的话，ZL=0，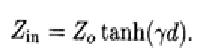

显然，要获得Zin，还必须求解正切函数。集总参数模型就是为了消除正切函数的复杂性。如果，

，

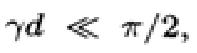那么，tanh(x)近似等于x，

所以，，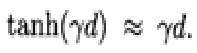

而Z0=sqrt [(R+jwL)/(G+jwC)],则Zin=R+jwL，R是长度为d的传输线的电阻，L是长度为d的传输线的电感。

如果负载开路的话，ZL=无穷大。，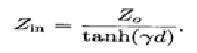

Zin=1/(G+jwC)]。由此，互联也可以同RLGC模型建立起来。

常用的几种互联的模型：a，T型；b，pi型；c，反tao型，d，tao型。

在9.8 a中的T型互联，它的输入阻抗是

，

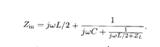如果我们假设Zin=ZL，则可以从负载端开始化简，那么，每一段的输入阻抗都是Zin=ZL，定义迭代阻抗Zi。Zi=Z0=ZL。

从上式可以得到

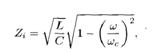
Wc=2/sqrt(LC)。Wc通过对Zin（不包含ZL的时候）求导得出。

如果采用T型结构对互联和传输线建模，我们可以知道，在低频端，Zi等于特性阻抗Z0；如果频率开始接近Wc，模型开始不够准确。为了保证迭代阻抗保持5%的精度，这个模型的带宽是

Pi型网络的带宽和T型的一样。对于tao型网络，w<0.1/sqrt(LC),这个值是上述带宽的1/6，所以，集总参数的模型有一定的频率使用范围，超过这个频率，模型将不在准确。

尺度的确认[1]

    以T型结构为例。为了保证5%的精度，W<0.62/sqrt(LC),如果信号的上升时间是Tr，假定最高频率Fmax=1/Tr。（对于一个数字信号，它的上升时间约为周期的10%，那么Fmax=1/Tr=1/0.1Tperiod=10f，即最高频率是时钟频率的10倍，考虑到数字信号的频率宽度，一个电路必须能够处理从基频～5倍基频的信号，才能保证信号通过系统不发生畸变，因此，用10f来估计是很保守，很可靠的）

我们得到：

2*pi*Fmax<0.62/sqrt(LC),所以Tr>2*pi* sqrt(LC)/0.62=10 sqrt(LC)。

而sqrt(LC)传输线的传播常数（时延），所以Tr>10Td。

这就是通常我们说的，集总参数模型的使用范围：传输线的长度要小于信号上升沿电气长度的1/10[1][3]，[2]中是1/6。

        到底是1/10还是1/6，并没有准确的定义，也有的工程师采用1/4，这完全取决于所要求的模型的精度，精度要求越高，这个集总参数模型的使用范围就越小。我个人比较喜欢1/6这个值，这是因为，在PCB上，信号沿着PCB走线传播的速度就是6in/ns，那么1/6上升沿的电气长度就是1in，这可以是我们有一个比较方便的估算值，即：信号上升时间(ns)=上升沿电气长度(in)。比如，如果信号的上升时间是2ns，那么集总参数模型的使用范围就是：传输线的长度小于2in。

-----------------------------第一章完-----------------------------------

Reference:

[1]Digital Signal Integrity-Modeling and Simulation with Interconnects and Package

[2]High-Speed Digital Design.  Howard Johnson

[3]High-Speed Digital System Design. Stephen. Hall

[4] Introduction to Electromagnetics Compatibility. Clayton R. Paul .Second Edition.English

[5] Electromagnetics Explained. Ron Schmitt

[6] Signal integrity— simplified / by Eric Bogatin

[7]信号完整性问题和印制电路版设计 Douglas Brooks

[8]泰克示波器基础原理培训教程和应用解决方案

[9]数字集成电路——设计透视 Jan M Rabaey