原创 频率和高速设计_3

5多高的频率范围对于高速数字设计才重要

    回到直观的问题上，到底多高的频率对高速设计来讲才重要？有了前面的讨论，可以知道，频率不是决定高速设计的主要因素，最主要的是上升时间。

若数字信号的上升时间定义为Tr，Fknee定义为转折频率；那么Fknee=0.5/Tr可作为一种衡量的标准。

由图可见，数字信号的大部分能量都集中于Fknee频率以下。在Fknee处，频谱的下降约为一半,这个值表征的是6dB的带宽，不同于前面定义的3dB带宽。用6dB带宽来估算更为保守一些，也更为准确。

从图中可以看出，一个信号如果能在Fknee频率以下的范围内顺利的通过，这个电路就对该频率的数字信号几乎不产生失真（因为大部分的能力都集中在Fknee以下，并且顺利通过了。）或者说该电路在该频率以下有一个平坦的响应。

平坦的响应是指系统在整个频率范围内有相同的幅度衰减和相位（群延时）；所有的频率都被放大或衰减相同的幅度，相移也相同。试想，如果我们要求信号通过一个系统没有衰减和相移，是不合理的，但如果作上面的合理要求和约束，这样的系统是可以实现的。这部分内容可以参考通信原理无失真传输的部分。

另一方面，如果在Fknee以下的频率响应是非平坦的，电路将对数字信号产生畸变，因为频率里面的主题部分并没有全部无失真的通过。

一个电路在Fknee以上的频率特性对它如何处理数字信号几乎是没有影响的。但是，！电磁辐射取决于Fknee频率以上部分的具体频谱情况，这个在EMC设计的时候要特别注意。

6.电尺寸[4]

   电尺寸是一个很重要的概念。本质上说，物理尺寸不重要。Although Maxwells equations govern all electrical phenomena,they are quit complicated, mathematically.Hence we use,where possible,simpler approxi mations to them such as lumped-circuit models and Kirchhoffs laws.The important question here is when we can use the simpler lumped-circuit models and Kirchhoff laws instead of Maxwells equations when analyzing a problem.

电尺寸使用波长来衡量的。假设V是波的传播速度，f是波的频率，那么波长y=V/f，很明显，波长表示了一个周期的时间内，波传播的距离。如果物理尺寸是L，那么，L和波长y的相对关系k=L/y=LV/f。

如果我们认为当物理尺寸远远小于一个波长的时候,即k<<1，该结构是电小尺寸，反之，是电大尺寸。那么，这就是一个近似的标准。问题是，用什么确定的标准来衡量，也就是说，当k小于波长小到什么程度的时候才能当作电小尺寸呢？

考虑上面的集总元件，当波从a点进入，从b点退出的时候，经历的时间是L/v。这段时间实际上是波通过一个集总元件的时延。

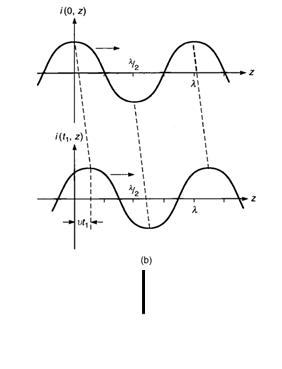
从上面的图可以看出，当距离L等于一个波长y时，波通过这个元件相位发生了360度改变，当L等于半个波长1/2y的时候，产生180度相位改变。如果是1/10，相位改变36度；如果是1/20，改变18度；如果是1/100,改变3.6度。

如果两个点之间的距离很小，也就是说可以按照集总参数模型来建模，那么这一小段距离带来的相位的改变是可以忽略的。

这一小段距离应该有多小？对此，并没有统一的标准，但是，我们假设，当物理尺寸小于波长的1/10时，相位的变化就可以忽略，这样的结构就被认为是电小尺寸。

    为了分析电路，我们需要确定一段结构的电尺寸。自由空间的光速是3x10^8m/s，300MHz时对应的波长是1m。记住这个参数很重要，这样，在自由空间中其他的频率对应的波长就很容易得到了，比如，50Mhz，对应6m，2GHz，对应15cm。如果波不是在自由空间中传播的呢？波在自由空间的波速由下式给出

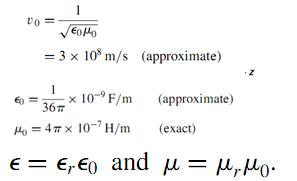
注意观察，e的单位是F，对应电容，u的单位是H，对应电感。在后面可以看到，传输线的传播时延是sqrt(LC)，因此，速度是1/ sqrt(LC)。只不过LC都是相对自由空间计算的值。所以，如果不在自由空间，就是用相对介电常数和相对磁导率来计算。

有两点需要注意：非铁磁材料的ur都是1，铁磁材料的er都是1.

         我们已经把物理尺寸和电尺寸建立了联系。电尺寸和波长紧密联系， 也就是和频率紧密联系，数字设计中的信号一般是方波，因此我们还需要把频率和上升时间或带宽联系起来。也就是说，需要建立一个物理尺寸和信号的上升时间的直观关系，使得在知道信号的上升时间的时候，我们能够快速的判断出一个电路到底是不是可以简化为集总参数模型。如果是，计算就可以大大简化，那真是太好了。