原创 STM32上256点的FFT傅里叶变换

STM32上256点的FFT傅里叶变换<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />

在STM32F10XX系列IC进行256点的FFT，发现效果还不错，波形正如预期所想，基本没发现什么大异常。

输入信号: X="1"+sin(2*pi*fo*t)

信号频率： 10KHZ

抽样频率： 48KHZ

抽样点数： 256

从上面输入的信号，可知， 正弦信号时叠加在一个直流分量为1V的信号之上，那么在进行FFT变换之后，所得频谱幅度应该在2V左右，并且频率为0，说明为直流分量。

在频谱10KHZ出将出现幅值幅度为1V左右的信号频率。

为了验证程序代码，先在MATLAB上实现仿真。

从MATLAB上仿真得到的结果，基本如上所述。

<?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" />

STM32的运算结果对比:

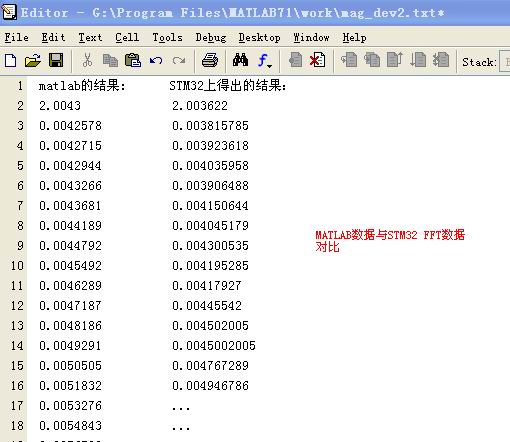
VC模拟运算也基本符合（^_^）

对比MATLAB，感觉波形还不错，基本一致！（大家可以从我的博客上下载到相关程序，进行对比）

上位机演示程序：

https://static.assets-stash.eet-china.com/album/old-resources/2010/6/21/37035672-d304-4904-b4d1-da09807c69de.rar 

MATLAB演示程序：

%by dz561
fs=48000;%设定采样频率
%N=128;
N=256;
n=0:N-1;
t=n/fs;
f0=10000;%设定正弦信号频率
x=1+sin(2*pi * f0*t);
figure(1);
subplot(211);
plot(t,x);%作正弦信号的时域波形
xlabel('t');
ylabel('y');
title('1+sin(2*pi * f0*t)');
grid;
%进行FFT变换并做频谱图
y=fft(x,N);%进行fft变换
mag=abs(y)/N*2;%求幅值   equal to: aqrt(real(X).^2 + imag(X).^2)
f=(0:length(y)-1)'*fs/length(y);%进行对应的频率转换
figure(1);
subplot(212);
plot(f,mag)
xlabel('频率(Hz)');
ylabel('幅值');
title('实际幅值');
grid;