NTC负温度系数热敏电阻
NTC热敏电阻是指具有负温度系数的热敏电阻。是使用单一高纯度材料、具有 接近理论密度结构的高性能陶瓷。因此,在实现小型化的同时,还具有电阻值、 温度特性波动小、对各种温度变化响应快的特点,可进行高灵敏度、高精度的 检测。本公司提供各种形状、特性的小型、高可靠性产品,可满足广大客户的 应用需求。
NTC负温度系数热敏电阻工作原理
NTC是Negative Temperature Coefficient 的缩写,意思是负的温度系数,泛指负温度系数很大的半导体材料或元器件,所谓NTC热敏电阻器就是负温度系数热敏电阻器。它是以锰、钴、镍和铜等金属氧化物为主要材料,采用陶瓷工艺制造而成的。这些金属氧化物材料都具有半导体性质,因为在导电方式上完全类似锗、硅等半导体材料。温度低时,这些氧化物材料的载流子(电子和孔穴)数目少,所以其电阻值较高;随着温度的升高,载流子数目增加,所以电阻值降低。NTC热敏电阻器在室温下的变化范围在10O~1000000欧姆,温度系数-2%~-6.5%。NTC热敏电阻器可广泛应用于温度测量、温度补偿、抑制浪涌电流等场合。
NTC负温度系数热敏电阻专业术语
零功率电阻值 RT(Ω)
RT指在规定温度 T 时,采用引起电阻值变化相对于总的测量误差来说可以忽略不计的测量功率测得的电阻值。
电阻值和温度变化的关系式为:
RT = RN expB(1/T – 1/TN)
RT :在温度 T ( K )时的 NTC 热敏电阻阻值。
RN :在额定温度 TN ( K )时的 NTC 热敏电阻阻值。
T :规定温度( K )。
B : NTC 热敏电阻的材料常数,又叫热敏指数。
exp :以自然数 e 为底的指数( e = 2.71828 …)。
该关系式是经验公式,只在额定温度 TN 或额定电阻阻值 RN 的有限范围内才具有一定的精确度,因为材料常数 B 本身也是温度 T 的函数。
额定零功率电阻值 R25 (Ω)
根据国标规定,额定零功率电阻值是 NTC 热敏电阻在基准温度 25 ℃ 时测得的电阻值 R25,这个电阻值就是 NTC 热敏电阻的标称电阻值。通常所说 NTC 热敏电阻多少阻值,亦指该值。
材料常数(热敏指数) B 值( K )
B 值被定义为:
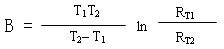
RT1 :温度 T1 ( K )时的零功率电阻值。
RT2 :温度 T2 ( K )时的零功率电阻值。
T1, T2 :两个被指定的温度( K )。
对于常用的 NTC 热敏电阻, B 值范围一般在 2000K ~ 6000K 之间。
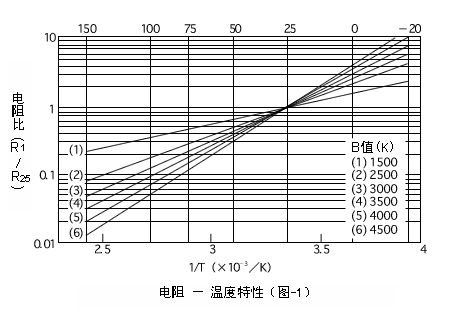
零功率电阻温度系数(αT )
在规定温度下, NTC 热敏电阻零动功率电阻值的相对变化与引起该变化的温度变化值之比值。
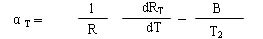
αT :温度 T ( K )时的零功率电阻温度系数。
RT :温度 T ( K )时的零功率电阻值。
T :温度( T )。
B :材料常数。
耗散系数(δ)
在规定环境温度下, NTC 热敏电阻耗散系数是电阻中耗散的功率变化与电阻体相应的温度变化之比值。
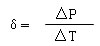
δ: NTC 热敏电阻耗散系数,( mW/ K )。
△ P : NTC 热敏电阻消耗的功率( mW )。
△ T : NTC 热敏电阻消耗功率△ P 时,电阻体相应的温度变化( K )。
热时间常数(τ)
在零功率条件下,当温度突变时,热敏电阻的温度变化了始未两个温度差的 63.2% 时所需的时间,热时间常数与 NTC 热敏电阻的热容量成正比,与其耗散系数成反比。
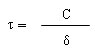
τ:热时间常数( S )。
C: NTC 热敏电阻的热容量。
δ: NTC 热敏电阻的耗散系数。
额定功率Pn
在规定的技术条件下,热敏电阻器长期连续工作所允许消耗的功率。在此功率下,电阻体自身温度不超过其最高工作温度。
最高工作温度Tmax
在规定的技术条件下,热敏电阻器能长期连续工作所允许的最高温度。即:
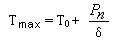
T0-环境温度。
测量功率Pm
热敏电阻在规定的环境温度下, 阻体受测量电流加热引起的阻值变化相对于总的测量误差来说可以忽略不计时所消耗的功率。
一般要求阻值变化大于0.1%,则这时的测量功率Pm为:
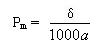
电阻温度特性
NTC热敏电阻的温度特性可用下式近似表示: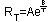
式中:
RT:温度T时零功率电阻值。
A:与热敏电阻器材料物理特性及几何尺寸有关的系数。
B:B值。
T:温度(k)。
更精确的表达式为:
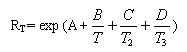
式中:RT:热敏电阻器在温度T时的零功率电阻值。
T:为绝对温度值,K;
A、B、C、D:为特定的常数。
热敏电阻的基本特性
电阻-温度特性
热敏电阻的电阻-温度特性可近似地用式1表示。
(式1) R="R"o exp {B(I/T-I/To)}
| R | : 温度T(K)时的电阻值 | | Ro | : 温度T0(K)时的电阻值 | | B | : B 值 | | *T(K)= t(oC)+273.15 |
但实际上,热敏电阻的B值并非是恒定的,其变化大小因材料构成而异,最大甚至可达5K/°C。因此在较大的温度范围内应用式1时,将与实测值之间存在一定误差。
此处,若将式1中的B值用式2所示的作为温度的函数计算时,则可降低与实测值之间的误差,可认为近似相等。
(式2) BT=CT2+DT+E
上式中,C、D、E为常数。
另外,因生产条件不同造成的B值的波动会引起常数E发生变化,但常数C、D 不变。因此,在探讨B值的波动量时,只需考虑常数E即可。
? 常数C、D、E的计算
常数C、D、E可由4点的(温度、电阻值)数据 (T0, R0). (T1, R1). (T2, R2) and (T3, R3),通过式3~6计算。
首先由式样3根据T0和T1,T2,T3的电阻值求出B1,B2,B3,然后代入以下各式样。
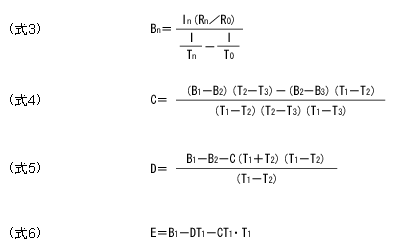
? 电阻值计算例
试根据电阻-温度特性表,求25°C时的电阻值为5(kΩ),B值偏差为50(K)的热敏电阻在10°C~30°C的电阻值。
? 步 骤
(1) 根据电阻-温度特性表,求常数C、D、E。 To=25+273.15 T1=10+273.15 T2=20+273.15 T3=30+273.15
(2) 代入BT=CT2+DT+E+50,求BT。
(3) 将数值代入R=5exp {(BTI/T-I/298.15)},求R。
*T : 10+273.15~30+273.15
? 电阻-温度特性图如图1所示
电阻温度系数
所谓电阻温度系数(α),是指在任意温度下温度变化1°C(K)时的零负载电阻变化率。电阻温度系数(α)与B值的关系,可将式1微分得到。
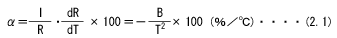
这里α前的负号(-),表示当温度上升时零负载电阻降低。
散热系数 (JIS-C2570)
散热系数(δ)是指在热平衡状态下,热敏电阻元件通过自身发热使其温度上升1°C时所需的功率。
在热平衡状态下,热敏电阻的温度T1、环境温度T2及消耗功率P之间关系如下式所示。
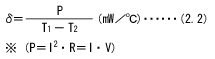
产品目录记载值为下列测定条件下的典型值。
| (1) | 25°C静止空气中。 | | (2) | 轴向引脚、经向引脚型在出厂状态下测定。 |
额定功率(JIS-C2570)
在额定环境温度下,可连续负载运行的功率最大值。
产品目录记载值是以25°C为额定环境温度、由下式计算出的值。
(式) 额定功率=散热系数×(最高使用温度-25)
最大运行功率
最大运行功率=t×散热系数 … (3.3)
这是使用热敏电阻进行温度检测或温度补偿时,自身发热产生的温度上升容许值所对应功率。(JIS中未定义。)容许温度上升t°C时,最大运行功率可由下式计算。
应环境温度变化的热响应时间常数(JIS-C2570)
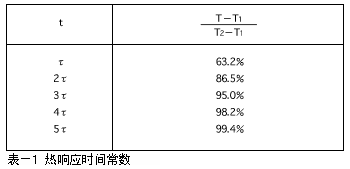
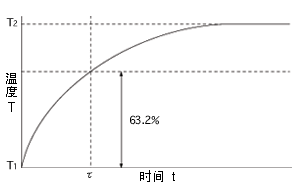
指在零负载状态下,当热敏电阻的环境温度发生急剧变化时,热敏电阻元件产生最初温度与最终温度两者温度差的63.2%的温度变化所需的时间。
热敏电阻的环境温度从T1变为T2时,经过时间t与热敏电阻的温度T之间存在以下关系。
| T= | (T1-T2)exp(-t/τ)+T2......(3.1) | | (T2-T1){1-exp(-t/τ)}+T1.....(3.2) |
常数τ称热响应时间常数。
上式中,若令t=τ时,则(T-T1)/(T2-T1)=0.632。
换言之,如上面的定义所述,热敏电阻产生初始温度差63.2%的温度变化所需的时间即为热响应时间常数。
经过时间与热敏电阻温度变化率的关系如下表所示。
产品目录记录值为下列测定条件下的典型值。
| (1) | 静止空气中环境温度从50°C至25°C变化时,热敏电阻的温度变化至34.2°C所需时间。 | | (2) | 轴向引脚、径向引脚型在出厂状态下测定。 |
另外应注意,散热系数、热响应时间常数随环境温度、组装条件而变化。
NTC负温度系数热敏电阻R-T特性
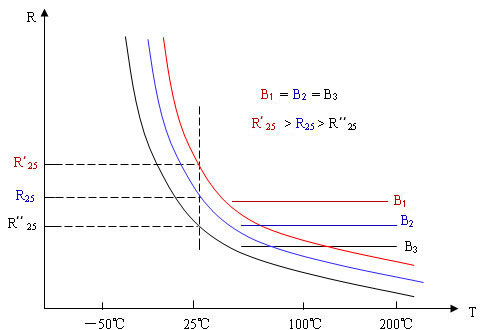
B 值相同, 阻值不同的 R-T 特性曲线示意图
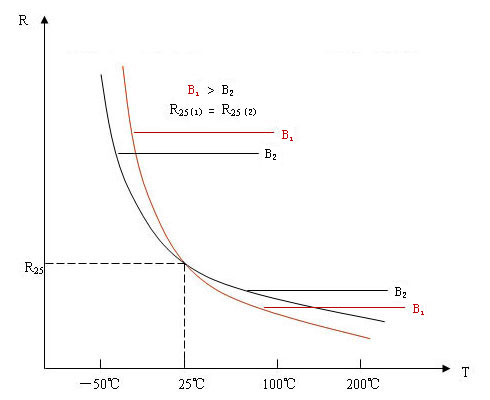
相同阻值,不同B值的NTC热敏电阻R-T特性曲线示意图
温度测量、控制用NTC热敏电阻器
外形结构
 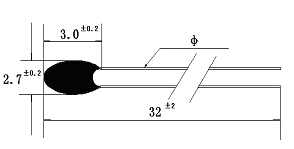
环氧封装系列NTC热敏电阻
 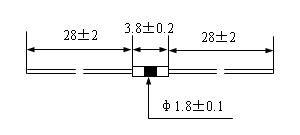
玻璃封装系列NTC热敏电阻
应用电路原理图
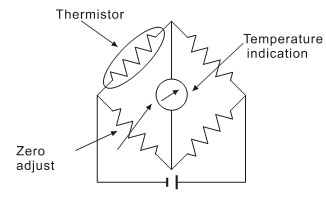
温度测量(惠斯登电桥电路)
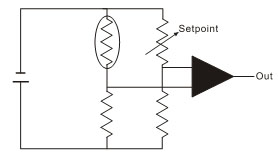
温度控制
应用设计
- 电子温度计、电子万年历、电子钟温度显示、电子礼品;
- 冷暖设备、加热恒温电器;
- 汽车电子温度测控电路;
- 温度传感器、温度仪表;
- 医疗电子设备、电子盥洗设备;
- 手机电池及充电电器。
温度补偿用NTC热敏电阻器<?XML:NAMESPACE PREFIX = O />
产品概述
许多半导体和ICs有温度系数而且要求温度补偿,以在较大的温度范围中达到稳定性能的作用,由于NTC热敏电阻器有较高的温度系数,所以广泛应用于温度补偿。
主要参数
额定零功率电阻值R25 (Ω)
R25允许偏差(%)
B值(25/50 ℃)/(K)
时间常数 ≤30S
耗散系数 ≥6mW/ ℃
测量功率 ≤0.1mW
额定功率 ≤0.5W
使用温度范围 -55 ℃ ~+125 ℃
降功耗曲线:
<?XML:NAMESPACE PREFIX = V />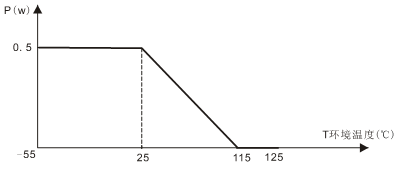 |
应用原理及实例
| 




 /3
/3 
文章评论(0条评论)
登录后参与讨论