原创 开关电源传递函数及状态平均化法

然而，虽然在这里计算出DC/DC转换器的传递函数这一主题，是通往“对各控制系统传递函数的通用化”课题的首要课题。

为了导出DC/DC转换器的传递函数，需要将开关工作周期的时间平均化，近似为线性工作。此外，导出的传递函数与降压、升压、升降压等电压转换的类型，电压模式或电流模式以及导通时间固定迟滞控制（也称为纹波控制、比较器控制等）等控制方法有所不同。大概是因此，各模式的方法不统一，结果总之处于烦杂的状况。

本章将结合目前为止导出的公式，首先导出作为基础的降压模式的开关传递函数，使用状态平均化法，来导出在工作模式中未特殊化且被统一的传递函数。

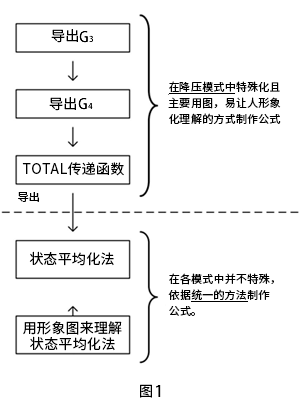
虽然之前已经简单的描述过，但我认为这是最难解且很难形象化示意的传递函数。因此，先将本章的描述流程总结在图1。

听到状态平均化法的话，总觉得可能会有很多人不了解。但是，使用此法的话，各转换器的传递函数就能根据统一的方法导出。这里我会尽可能用简单易懂的方式来描述，所以大家先挑战看看吧。

G3传递函数导出、频率特性

首先，我们有必要重温根据每个功能来对开关稳压器进行模块划分。在这里，先导出与开关模块的G3相关的传递函数。

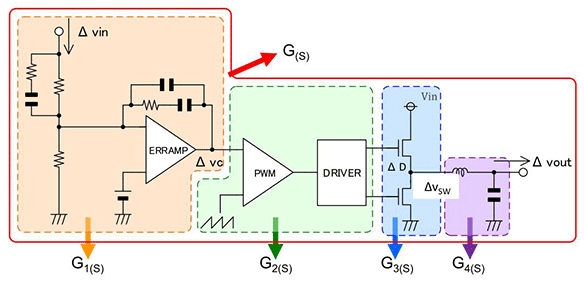
首先，来计算出。请看图2。

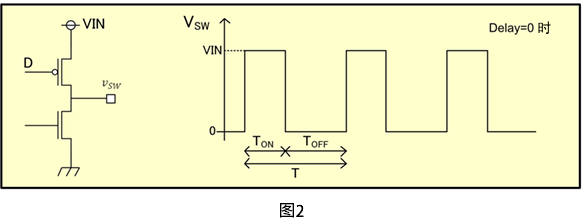
这就是降压模式的开关波形。VSW可用SW端子作为H(VIN)，L(O)的时间平均来描述，

因此，在公式4-1中，假设D→D+∆D、VSW→VSW+∆VSW的话，

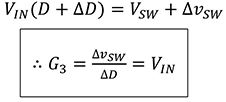
那么可导出。

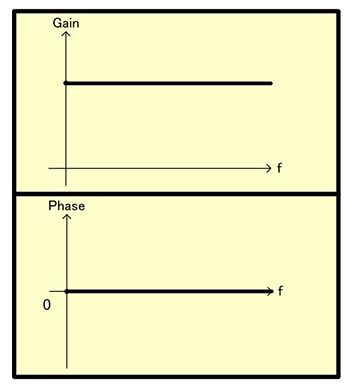
这个结果如下图所示，G3表示Gain一定相位不发生变化。

G4传递函数的导出

接着将计算输出的滤波器模块G4、。请看图4。

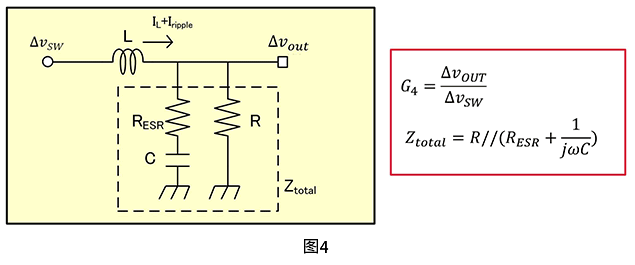
上图表示从VSW经过LC滤波器与Vout连接的路径。从VSW开始看，可以认为Vout是L和Ztotal的阻抗的阻抗划分，因此就可以导出以下公式4-2。

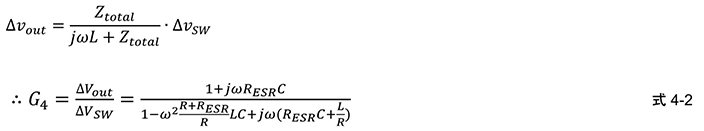
在这里，将在本G4的传递函数数基础上，考虑以下两种案例。

案例1

如果，RESR=0、R=open(∞) 的话，G4则变为如下。

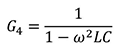
在经常见到的LC滤波器中，波特图如右图。这样的话，我想应该很快就能有印象。

f变小时，G4会变为正（＞0）值，因此Phase通常为0。

f变大时，变为的话，分母为0，因此Gain发散。

另外，f变大的话，G4会变为负（＜0）值，因此Phase将180°旋转。

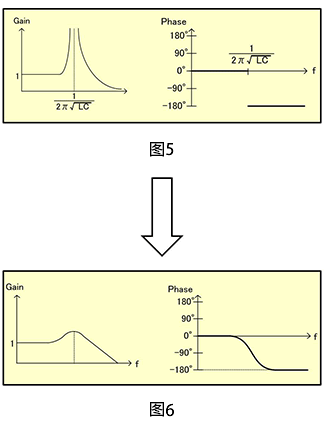
案例2

在案例1增加RESR和R，分母则加上1次虚数项。特别小或者特别大时，虽然和案例1相同，但是在f的谐振点附近，分母不会变为0，因此Gain不发散。

此时，在这里还残留着1次虚数项，因此相位不会0→180°，而是0→90°→180°这样变化。用波特图表示这一过程的就是图6。

G4的传递函数和波特图的关联，现在能有点印象了。

TOTAL传递函数（降压电压模式一般公式）

从这里开始将结合目前为止导出的传递函数，计算出作为整体的TOTAL传递函数。TOTAL的传递函数之前已介绍过，可以用以下公式来表示。

在此公式基础上，G可以写成如下形式。

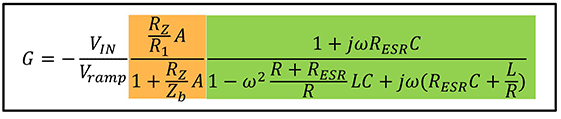
本公式的波特图如图7所示，可以看出各模块特征。并用不同的颜色表示各公式和图表的各区框。

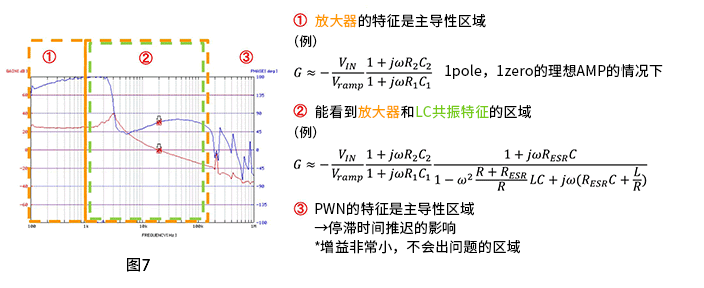
像这样根据每个模块来描述制作传递函数公式的话，就可以画出系统的波特图。但是，目前为止的论述都是先以有印象为主简单描述，因此会有不是很严密的部分。那是，G3和G4的导出部分，这种思路可适用于降压模式，但是却不适用于升压及升降压模式。因此，需要能适应这些所有的模式，状态平均化的思路。

上一章按开关电源的方框图讲述了传递函数及其相关公式。然而，为了让大家尽快对此有个整体了解，仅简单地介绍了虽然适用于降压模式、但不适用升压及升降压模式的公式。为了导出可适用所有模式的传递函数，本章将引入“状态空间平均法”的概念。

状态空间平均法

状态空间平均法可能稍微有些难度。但是，如果能理解这个概念，就应该能够导出各模式的传递函数。

首先，状态空间平均法是：

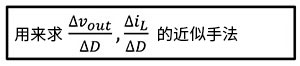
请牢牢记住这点。

图8是降压模式、升压模式、升降压模式的方框图以及各模式的共通部分和不同部分。如图所示，不同的部分只有。

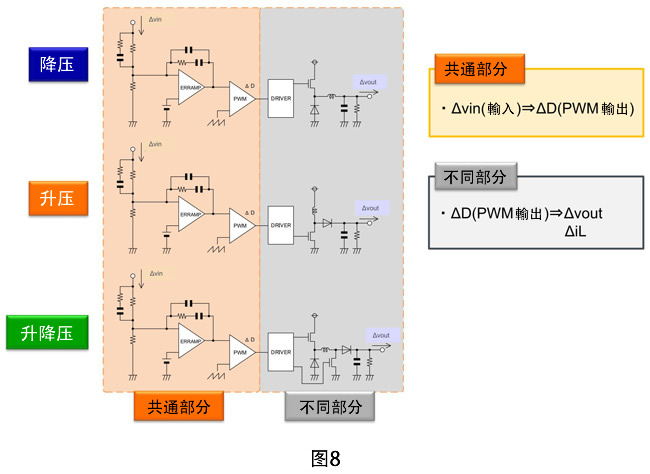
接下来具体介绍一下如何使用状态空间平均法。可使用“状态空间平均法”的前提是“1个周期内的状态变化量很小”。在这个前提成立的情况下，“1个周期的状态变化量为SWON时的状态变化量和SWOFF时的状态变化量的各自线形近似”，可表示如下。

DCDC转换器的情况下，一般选择线圈电流和输出电容器的电荷量作为状态变量。 具体以降压转换器为例表示如下。

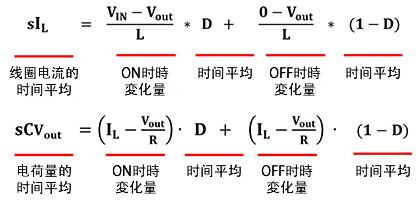
s表示拉普拉斯变换，此后可以认为s=jω。未完待续。

上一章为导出适用于降压、升压、升降压所有模式的传递函数，介绍了“状态空间平均法”。本章将以导出的公式为基础进行静态分析。由于需要使用上一章的公式，因此结合上一章的内容会更容易理解。

静态分析

第一行为上一章导出的线圈电流和电容器的电荷量公式。

将以这些公式为基础进行静态分析。在静态（正常状态/稳定状态)下，线圈电流的变化量、输出电容器的电荷变化量均为0（零），因此第二行是代入0的公式。D被改写为时间。

整理一下这些公式，得到第3行公式4-22和4-23。

公式4-22就是众所周知的VIN、Vout、D 的关系式。

公式4-23表示线圈电流的平均值　在1个周期内被供给输出负载。

该思路不仅适用降压转换器，还适用于升压转换器和升降压转换器。

现将各转换器的静态工作汇总如下。

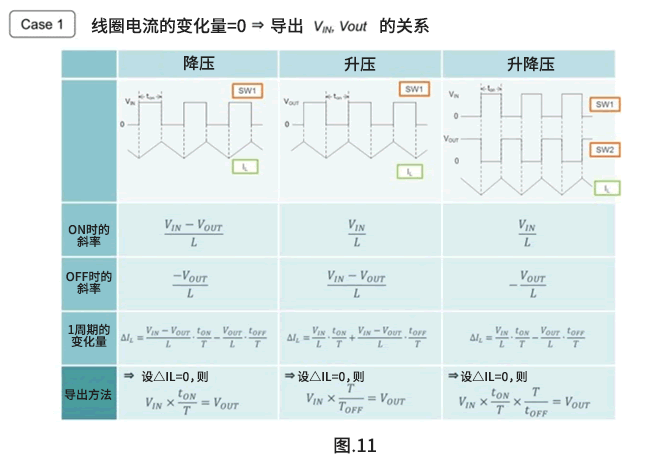
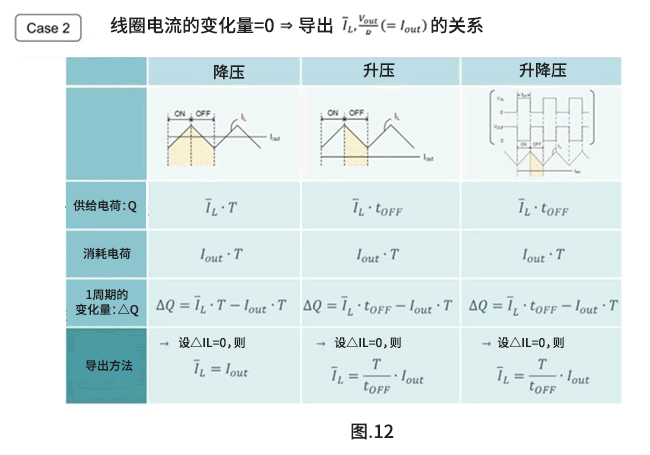
上一章利用“状态空间平均法”导出的公式进行了静态分析。本章将进行动态分析，以引出状态空间平均法的目的–。请结合上一章静态分析的内容一并阅读。

动态分析

下面是之前导出的线圈电流和电容器的电荷量的相关公式。多次强调过，请以这是前提来思考，否则很难对公式进行解说。

对每个公式进行的步骤相同，分别表述如下。

这样，只要将最后的公式相结合，即可求出。再次给出公式：

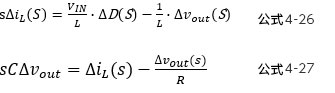
下一章将针对该公式的导出，稍微换个角度来看一下。

上一章通过动态分析导出了用来得出状态空间平均法的目的 的公式。本章将从另外的角度来看上一章导出的公式的导出方法。前提是至少已经理解了之前导出公式的原理原则。 由于需要上一章的公式创建过程和各个公式，因此本章将使用同样的公式。

下面是上一章提到的动态分析。之前导出的线圈电流和电容器的电荷量相关的公式如下。请再来看一遍。　　　　　

与上一章相同，这里也给出了最后的公式，就像之前提到的一样，只要将这些公式相结合，即可求出 

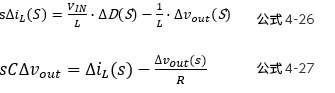
接下来将是本章的内容。以下的公式4-28、4-29是将阻抗S表述为 的公式。

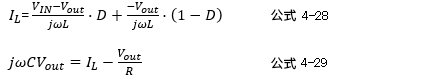
这里 ，整理如下。

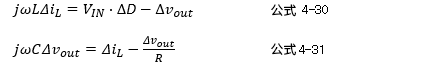
这些公式得出的结果与上一章导出的公式4-26、4-27相同。

思路如下：

① 考虑系统的稳定状态
  1) 线圈电流在1周期内不变
  2) 电容器的电荷量在1周期内不变
  ※此时，阻抗表述为 

②，求

只要按这样的思路理解了原理原则，即可比较简单地求出 。

关于状态空间平均法的介绍到此接近尾声，状态空间平均法属于近似法，因此请不要忘记一定要考虑应用范围和适用条件，这是非常重要的。

来源：techclass.rohm