


传递函数
传递函数是指,是“表示系统的输入和输出的关系性,输入转换为输出的函数”。 从这里起如果符合思考的话可以说“通过黑匣子输入信号(vin)被变换为输出信号(vout)时的变换变量”。
作为通常的传递函数所示的重要因素的有增益和相位。增益表示传递路径的增幅率,相位表示传递时间的偏差。简化它们,并总结在图1中。
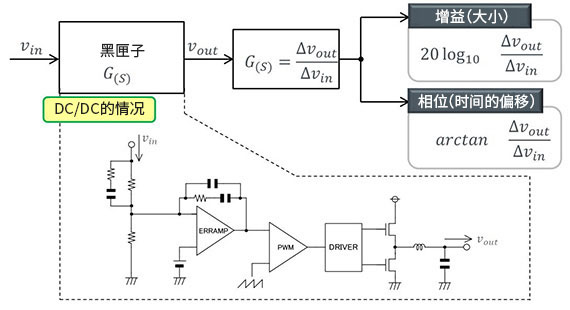
图 1
说起“增益和相位”,对从事模拟系统的人首先浮现在脑海中的大概是运算放大器的特性。正如所说,如果运算放大器作为黑匣子考虑,用传递函数可以表现运算放大器的增益和相位的特性。
关于DC/DC转换器,瞬态响应特性的评价中增益和相位的特性的测定被熟知。DC/DC转换器时,也认为是DC/DC转换器作为黑匣子表示增益和相位的传递函数。图1中虚线包围的电路,是DC/DC转换器时的内部为黑匣子的一个例子。
传递函数导出的基础概念
在以图1为基础计算传递函数时,传递函数有方便的特点。那就是传递函数可以分解,以它们的积来描述。具体例子如图2所示。
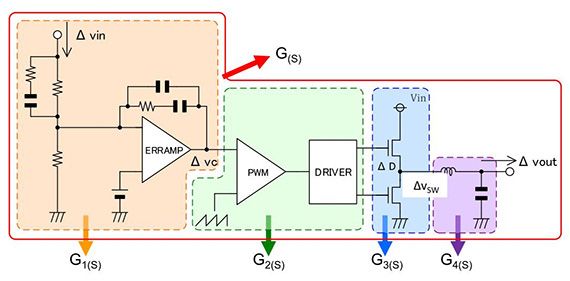
图 2
图2是指图1的DC/DC转换器的内部是黑匣子,红线包围的整体作为G(S),将每个模块分解为G1(S) 、G2(S) 、G3(S) 、G4(S)后可以描述为如下的公式1-1。
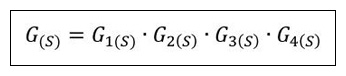
公式 1-1
例如,G1(S)是指误差放大器模块的传递函数,对于输入Δvin输出Δvc可以表示为Δvc / Δvin,各模块可以如下表示。
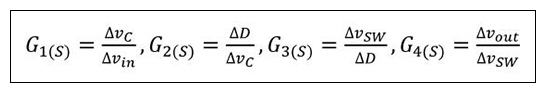
这里套用公式1-1
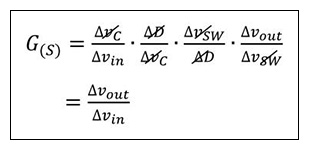
公式 1-2
得出公式1-2,可以看出公式1-1是正确。
也就是说,导出各模块的传递函数,通过取得它们的积可以计算出作为整体的传递函数。
以各模块计算具体的传递函数之前,在导出传递函数时,确认两个重要的定律。
一个是指基尔霍夫的电流定律。本定律是指“任意的节点中电流的和为0”。本定律必须要注意的是电流的流向。
另一个是指基尔霍夫的电压定律。本定律是指“任意的闭合电路中电压波动为0”。这两个定律如图3所示。
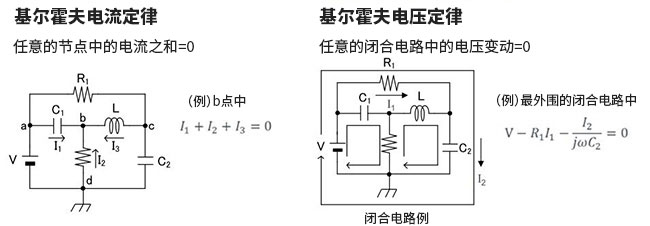
图3
为了导出传递函数而使用上面两个定律,但是有一件事必须要探讨。那就是如何表述阻抗。如下面的图4所示,电阻R、电容C、线圈L连接于DC电源V,各自的变动不同。电阻R两端的电压不随时间的推移变化。电容器的电压逐步上升,一定时间后达到电源的电压。 线圈的电压立刻达到电源的电压,逐步下降。
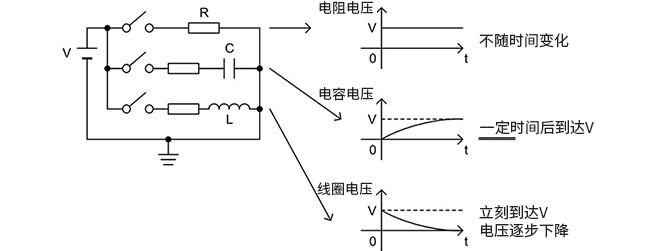
图4
从图4的特性可以认为,以电容器和线圈以及电阻考虑时,电阻值(阻抗)可以作为时间(相位)的函数。这样,包括随时间变化的电阻,都可以表述为阻抗。可以说输入电压为步进响应时的电容器的阻抗随时间的推移变大。线圈与其相反。电路的场合,因为作为时间的倒数而使用角速度ω、可以表示为如图5所示。
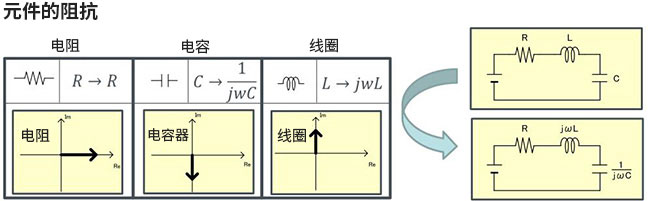
图5
最后,解释出现复数的原因。电路中复数表示相位,是响应时间相关的参数。这种情况,表示电源的响应速度。电容器的情况为延迟后到达电源电压V,线圈与其相反,可以表示为如图5所示。
频率特性
传递函数的频率特性
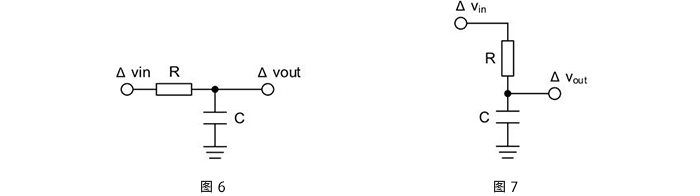
首先,请看图6。电阻和电容器组成简单的闭合电路。首先,尝试计算出本电路的传递函数。
为了让电路图容易形象化,将图6改画成图7。当然,作为电路是相同的。这样一来,能立刻明白ΔVout是ΔVin通过R和C的阻抗分割的。
形成公式ΔVout = ΔVin ×(C/(R+C)),表示阻抗。
正如前项的“基尔霍夫定律和阻抗”说明的那样,虽然R的表示为R,

然后尝试画波特图。波特图是指横轴为频率(⨍),纵轴为增益(Gain)和相位(Phase)的图表,需要计算按增益和相位。首先,从增益开始计算。
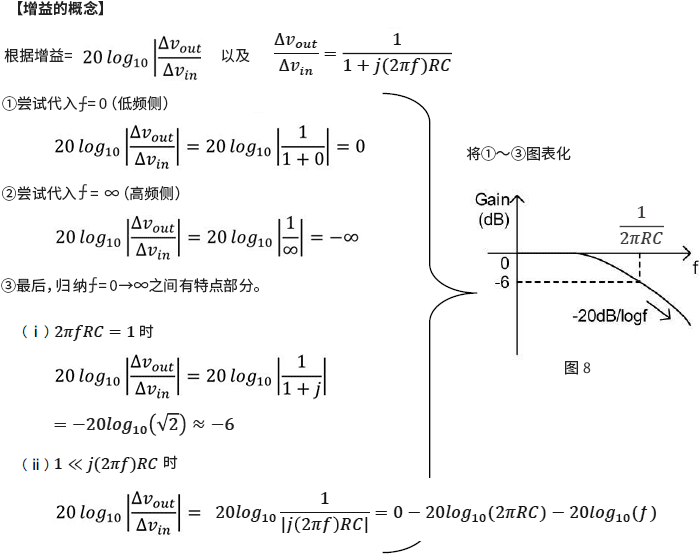
接着,计算相位。

总结上述,如下面的图10所示。至此,可以让增益(Gain)和相位(Phase)的特性形象化。
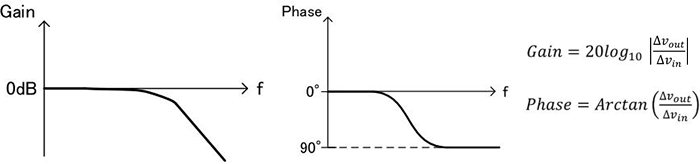
图10
前项“基尔霍夫定律和阻抗”中,讲述了电容器的阻抗表示为“1/jωC”,以达到理解传递函数的目的。请看图11。
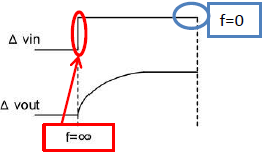
图11是指图6的电路的步进响应特性。电容器电源波动的瞬间(与f = ∞等值),电容器的阻抗为0,ΔVout=0。经过一定时间变为(与f=∞等值)ΔVin相等。
接着,图形化如下。这是电容器步进响应针对阻抗“1/jωC”的示意图。

图12
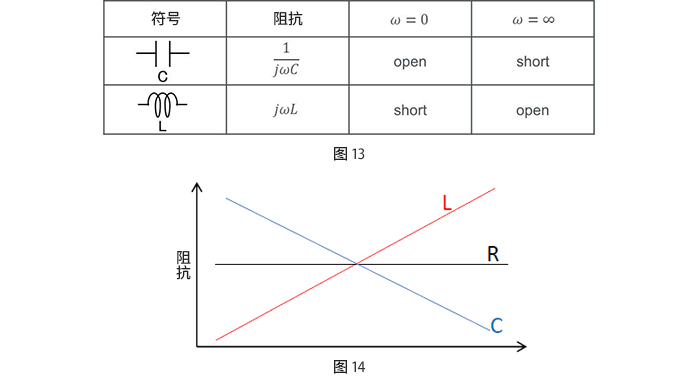
图13中包括线圈的各元件的阻抗记述和ω=0以及ω=∞时的等价处理,而且,图14中表示频率特性。
 /4
/4 
文章评论(0条评论)
登录后参与讨论