原创 传输线_6

3 传输线上的信号完整性

    从前面的推导可以知道，如果负载和传输线的特性阻抗不相等，反射系数就不为0，线路上就存在着反射电压；同样，把电压源的内阻看成是负载的话，如果不与传输线的特性阻抗相等，也存在着反射电压。很明显，这时候得到的一定不是理想波形。线路上的非理想的电压波形到底会不会对接受产生影响，这是一个重要的问题。因此，需要对反射的问题做一些讨论。

    尽管传输线的方程能获得结论，但它也比较复杂。我们需要把信号完整性的问题进一步简化，既便于理解，又便于记忆。

当一个信号施加在传输线的一端时，电压的一部分向下传播。A(w)是输入接受函数，它由源端阻抗，传输线阻抗决定。<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />

A(w)=Zo/(Zs+Zo)。可以用电阻的分压原理来理解这个公式。这样，初始加到传输线上的电压就是V0*A(w)=Vo*Zo/(Zs+Zo)。

随着信号的传播，它受到传播函数的H(w)的衰减H(w)的表达式前面我们已经得到了。

有关该公式可参考[3]的内容（pp-90）。R(w)是走线的串联电阻，由于趋麸效应的影响，它是频率的函数。X是走线的长度。传播时延是复数，实部部分代表了衰减的常数，虚数部分代表了相位常数。

    在传输线的远端，出现一个信号衰减后的部分振幅T(w)。T(w)=2*ZL/(ZL+Z0)。当信号的T(w)部分出现在远端的时候，一个反射信号沿着电缆反向传播。返回源端的信号R₂(w)，就是反射系数。前面已经给出了。当信号返回源端的时候，再一次被H(w)衰减，并在源端第二次反射，反射系数R₁(w)在前面也已经给出了。从源端发射回来之后，再一次被H(w)衰减……无止境的循环下去。

这些表达式前面都已经求解过了。

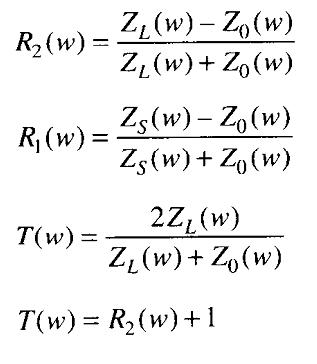
那么，当一个初始电压发送到传输线上，原始信号通过A(w),H(w),T(w)后，第一次在负载处得到S₀(w)=A(w)H(w)T(w)。然后，在负载端反射，传播到源端，在源端发射，在传播回负载端。第二次出现在负载端的信号是：

S₁(w)= A(w)H(w)R₂(w) H(w) R₁(w)H(w)T(w)= A(w)H(w)[ R₂(w) H(w)² R₁(w)] T(w),

然后再一次重复这样的过程。Sn是一个等比级数，它的极限求和得到如下表达式：

这是一个传输系统从源端到负载端的频率响应。可以看得出来，最后出现在负载端（接收端）的信号是经过了多次反射(R1,R2)以及线路的衰减(H(w))之后的信号。

负载端最后的响应和A(w), H(w), R₁(w)，R₂(w)有联系。由于R1和R2的存在，波形不是我们需要的理想的波形，而是多次反射之后的一个稳态值。这样的波形可能会影响接收器的接受。我们必须想办法改善。