


新学期开始了,开始专心于技术上了,上学期的寒假总是那么短暂,飘飘乎就这样逝去,今天补补上学期还没学完的数据结构---图,希望能和大家一起探讨,共同进步~
定义:
图是由顶点集合及顶点间的关系集合组成的一种数据结构。
图的存储结构:
1.1 邻接矩阵
图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(邻接矩阵)存储图中的边或弧的信息。
设图G有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
![]()
看一个实例,下图左就是一个无向图。
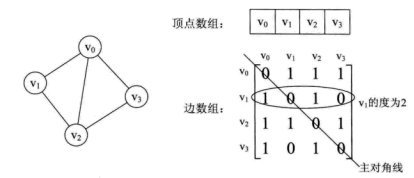
从上面可以看出,无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足aij = aji。即从矩阵的左上角到右下角的主对角线为轴,右上角的元和左下角相对应的元全都是相等的。
从这个矩阵中,很容易知道图中的信息。
(1)要判断任意两顶点是否有边无边就很容易了;
(2)要知道某个顶点的度,其实就是这个顶点vi在邻接矩阵中第i行或(第i列)的元素之和;
(3)求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍,arc[j]为1就是邻接点;
而有向图讲究入度和出度,顶点vi的入度为1,正好是第i列各数之和。顶点vi的出度为2,即第i行的各数之和。
若图G是网图,有n个顶点,则邻接矩阵是一个n*n的方阵,定义为:
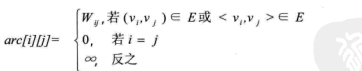
这里的wij表示(vi,vj)上的权值。无穷大表示一个计算机允许的、大于所有边上权值的值,也就是一个不可能的极限值。下面左图就是一个有向网图,右图就是它的邻接矩阵。
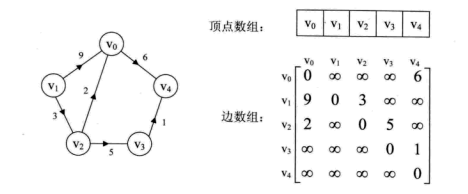
那么邻接矩阵是如何实现图的创建的呢?代码如下。
1 #include <stdio.h> 2 #include <stdlib.h> 3 #include <curses.h> 4 5 typedef char VertexType; //顶点类型应由用户定义 6 typedef int EdgeType; //边上的权值类型应由用户定义 7 8 #define MAXVEX 100 //最大顶点数,应由用户定义 9 #define INFINITY 65535 //用65535来代表无穷大 10 #define DEBUG 11 12 typedef struct 13 { 14 VertexType vexs[MAXVEX]; //顶点表 15 EdgeType arc[MAXVEX][MAXVEX]; //邻接矩阵,可看作边 16 int numVertexes, numEdges; //图中当前的顶点数和边数 17 }Graph; 18 19 //定位 20 int locates(Graph *g, char ch) 21 { 22 int i = 0; 23 for(i = 0; i < g->numVertexes; i++) 24 { 25 if(g->vexs == ch) 26 { 27 break; 28 } 29 } 30 if(i >= g->numVertexes) 31 { 32 return -1; 33 } 34 35 return i; 36 } 37 38 //建立一个无向网图的邻接矩阵表示 39 void CreateGraph(Graph *g) 40 { 41 int i, j, k, w; 42 printf("输入顶点数和边数:\n"); 43 scanf("%d,%d", &(g->numVertexes), &(g->numEdges)); 44 45 #ifdef DEBUG 46 printf("%d %d\n", g->numVertexes, g->numEdges); 47 #endif 48 49 for(i = 0; i < g->numVertexes; i++) 50 { 51 g->vexs = getchar(); 52 while(g->vexs == '\n') 53 { 54 g->vexs = getchar(); 55 } 56 } 57 58 #ifdef DEBUG 59 for(i = 0; i < g->numVertexes; i++) 60 { 61 printf("%c ", g->vexs); 62 } 63 printf("\n"); 64 #endif 65 66 67 for(i = 0; i < g->numEdges; i++) 68 { 69 for(j = 0; j < g->numEdges; j++) 70 { 71 g->arc[j] = INFINITY; //邻接矩阵初始化 72 } 73 } 74 for(k = 0; k < g->numEdges; k++) 75 { 76 char p, q; 77 printf("输入边(vi,vj)上的下标i,下标j和权值:\n"); 78 79 p = getchar(); 80 while(p == '\n') 81 { 82 p = getchar(); 83 } 84 q = getchar(); 85 while(q == '\n') 86 { 87 q = getchar(); 88 } 89 scanf("%d", &w); 90 91 int m = -1; 92 int n = -1; 93 m = locates(g, p); 94 n = locates(g, q); 95 if(n == -1 || m == -1) 96 { 97 fprintf(stderr, "there is no this vertex.\n"); 98 return; 99 } 100 //getchar(); 101 g->arc[m][n] = w; 102 g->arc[n][m] = g->arc[m][n]; //因为是无向图,矩阵对称 103 } 104 } 105 106 //打印图 107 void printGraph(Graph g) 108 { 109 int i, j; 110 for(i = 0; i < g.numVertexes; i++) 111 { 112 for(j = 0; j < g.numVertexes; j++) 113 { 114 printf("%d ", g.arc[j]); 115 } 116 printf("\n"); 117 } 118 } 119 120 int main(int argc, char **argv) 121 { 122 Graph g; 123 124 //邻接矩阵创建图 125 CreateGraph(&g); 126 printGraph(g); 127 return 0; 128 }
从代码中可以得到,n个顶点和e条边的无向网图的创建,时间复杂度为O(n + n2 + e),其中对邻接矩阵Grc的初始化耗费了O(n2)的时间。
1.2 邻接表
邻接矩阵是不错的一种图存储结构,但是,对于边数相对顶点较少的图,这种结构存在对存储空间的极大浪费。因此,找到一种数组与链表相结合的存储方法称为邻接表。
邻接表的处理方法是这样的:
(1)图中顶点用一个一维数组存储,当然,顶点也可以用单链表来存储,不过,数组可以较容易的读取顶点的信息,更加方便。
(2)图中每个顶点vi的所有邻接点构成一个线性表,由于邻接点的个数不定,所以,用单链表存储,无向图称为顶点vi的边表,有向图则称为顶点vi作为弧尾的出边表。
例如,下图就是一个无向图的邻接表的结构。
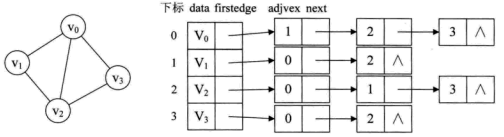
从图中可以看出,顶点表的各个结点由data和firstedge两个域表示,data是数据域,存储顶点的信息,firstedge是指针域,指向边表的第一个结点,即此顶点的第一个邻接点。边表结点由adjvex和next两个域组成。adjvex是邻接点域,存储某顶点的邻接点在顶点表中的下标,next则存储指向边表中下一个结点的指针。
对于带权值的网图,可以在边表结点定义中再增加一个weight的数据域,存储权值信息即可。如下图所示。
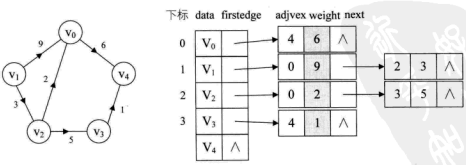
对于邻接表结构,图的建立代码如下。
1 /* 邻接表表示的图结构 */ 2 #include <stdio.h> 3 #include<stdlib.h> 4 5 #define DEBUG 6 #define MAXVEX 1000 //最大顶点数 7 typedef char VertexType; //顶点类型应由用户定义 8 typedef int EdgeType; //边上的权值类型应由用户定义 9 10 typedef struct EdgeNode //边表结点 11 { 12 int adjvex; //邻接点域,存储该顶点对应的下标 13 EdgeType weigth; //用于存储权值,对于非网图可以不需要 14 struct EdgeNode *next; //链域,指向下一个邻接点 15 }EdgeNode; 16 17 typedef struct VertexNode //顶点表结构 18 { 19 VertexType data; //顶点域,存储顶点信息 20 EdgeNode *firstedge; //边表头指针 21 }VertexNode, AdjList[MAXVEX]; 22 23 typedef struct 24 { 25 AdjList adjList; 26 int numVertexes, numEdges; //图中当前顶点数和边数 27 }GraphList; 28 29 int Locate(GraphList *g, char ch) 30 { 31 int i; 32 for(i = 0; i < MAXVEX; i++) 33 { 34 if(ch == g->adjList.data) 35 { 36 break; 37 } 38 } 39 if(i >= MAXVEX) 40 { 41 fprintf(stderr,"there is no vertex.\n"); 42 return -1; 43 } 44 return i; 45 } 46 47 //建立图的邻接表结构 48 void CreateGraph(GraphList *g) 49 { 50 int i, j, k; 51 EdgeNode *e; 52 EdgeNode *f; 53 printf("输入顶点数和边数:\n"); 54 scanf("%d,%d", &g->numVertexes, &g->numEdges); 55 56 #ifdef DEBUG 57 printf("%d,%d\n", g->numVertexes, g->numEdges); 58 #endif 59 60 for(i = 0; i < g->numVertexes; i++) 61 { 62 printf("请输入顶点%d:\n", i); 63 g->adjList.data = getchar(); //输入顶点信息 64 g->adjList.firstedge = NULL; //将边表置为空表 65 while(g->adjList.data == '\n') 66 { 67 g->adjList.data = getchar(); 68 } 69 } 70 //建立边表 71 for(k = 0; k < g->numEdges; k++) 72 { 73 printf("输入边(vi,vj)上的顶点序号:\n"); 74 char p, q; 75 p = getchar(); 76 while(p == '\n') 77 { 78 p = getchar(); 79 } 80 q = getchar(); 81 while(q == '\n') 82 { 83 q = getchar(); 84 } 85 int m, n; 86 m = Locate(g, p); 87 n = Locate(g, q); 88 if(m == -1 || n == -1) 89 { 90 return; 91 } 92 #ifdef DEBUG 93 printf("p = %c\n", p); 94 printf("q = %c\n", q); 95 printf("m = %d\n", m); 96 printf("n = %d\n", n); 97 #endif 98 99 //向内存申请空间,生成边表结点 100 e = (EdgeNode *)malloc(sizeof(EdgeNode)); 101 if(e == NULL) 102 { 103 fprintf(stderr, "malloc() error.\n"); 104 return; 105 } 106 //邻接序号为j 107 e->adjvex = n; 108 //将e指针指向当前顶点指向的结构 109 e->next = g->adjList[m].firstedge; 110 //将当前顶点的指针指向e 111 g->adjList[m].firstedge = e; 112 113 f = (EdgeNode *)malloc(sizeof(EdgeNode)); 114 if(f == NULL) 115 { 116 fprintf(stderr, "malloc() error.\n"); 117 return; 118 } 119 f->adjvex = m; 120 f->next = g->adjList[n].firstedge; 121 g->adjList[n].firstedge = f; 122 } 123 } 124 125 126 void printGraph(GraphList *g) 127 { 128 int i = 0; 129 #ifdef DEBUG 130 printf("printGraph() start.\n"); 131 #endif 132 133 while(g->adjList.firstedge != NULL && i < MAXVEX) 134 { 135 printf("顶点:%c ", g->adjList.data); 136 EdgeNode *e = NULL; 137 e = g->adjList.firstedge; 138 while(e != NULL) 139 { 140 printf("%d ", e->adjvex); 141 e = e->next; 142 } 143 i++; 144 printf("\n"); 145 } 146 } 147 148 int main(int argc, char **argv) 149 { 150 GraphList g; 151 CreateGraph(&g); 152 printGraph(&g); 153 return 0; 154 }
对于无向图,一条边对应都是两个顶点,所以,在循环中,一次就针对i和j分布进行插入。
本算法的时间复杂度,对于n个顶点e条边来说,很容易得出是O(n+e)。
1.3 十字链表
对于有向图来说,邻接表是有缺陷的。关心了出度问题,想了解入度就必须要遍历整个图才知道,反之,逆邻接表解决了入度却不了解出度情况。下面介绍的这种有向图的存储方法:十字链表,就是把邻接表和逆邻接表结合起来的。
重新定义顶点表结点结构,如下所示。
![]()
其中firstin表示入边表头指针,指向该顶点的入边表中第一个结点,firstout表示出边表头指针,指向该顶点的出边表中的第一个结点。
重新定义边表结构,如下所示。
![]()
其中,tailvex是指弧起点在顶点表的下表,headvex是指弧终点在顶点表的下标,headlink是指入边表指针域,指向终点相同的下一条边,taillink是指边表指针域,指向起点相同的下一条边。如果是网,还可以增加一个weight域来存储权值。
比如下图,顶点依然是存入一个一维数组,实线箭头指针的图示完全与邻接表相同。就以顶点v0来说,firstout指向的是出边表中的第一个结点v3。所以,v0边表结点hearvex = 3,而tailvex其实就是当前顶点v0的下标0,由于v0只有一个出边顶点,所有headlink和taillink都是空的。
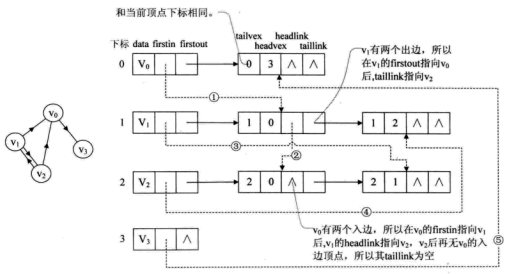
重点需要解释虚线箭头的含义。它其实就是此图的逆邻接表的表示。对于v0来说,它有两个顶点v1和v2的入边。因此的firstin指向顶点v1的边表结点中headvex为0的结点,如上图圆圈1。接着由入边结点的headlink指向下一个入边顶点v2,如上图圆圈2。对于顶点v1,它有一个入边顶点v2,所以它的firstin指向顶点v2的边表结点中headvex为1的结点,如上图圆圈3。
十字链表的好处就是因为把邻接表和逆邻接表整合在一起,这样既容易找到以v为尾的弧,也容易找到以v为头的弧,因而比较容易求得顶点的出度和入度。
而且除了结构复杂一点外,其实创建图算法的时间复杂度是和邻接表相同的,因此,在有向图应用中,十字链表是非常好的数据结构模型。
这里就介绍以上三种存储结构,除了第三种存储结构外,其他的两种存储结构比较简单。
二、图的遍历
图的遍历和树的遍历类似,希望从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫图的遍历。
对于图的遍历来说,如何避免因回路陷入死循环,就需要科学地设计遍历方案,通过有两种遍历次序方案:深度优先遍历和广度优先遍历。
2.1 深度优先遍历
深度优先遍历,也有称为深度优先搜索,简称DFS。其实,就像是一棵树的前序遍历。
它从图中某个结点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问,则另选图中一个未曾被访问的顶点作起始点,重复上述过程,直至图中的所有顶点都被访问到为止。
我们用邻接矩阵的方式,则代码如下所示。
1 #define MAXVEX 100 //最大顶点数 2 typedef int Boolean; //Boolean 是布尔类型,其值是TRUE 或FALSE 3 Boolean visited[MAXVEX]; //访问标志数组 4 #define TRUE 1 5 #define FALSE 0 6 7 //邻接矩阵的深度优先递归算法 8 void DFS(Graph g, int i) 9 { 10 int j; 11 visited = TRUE; 12 printf("%c ", g.vexs); //打印顶点,也可以其他操作 13 for(j = 0; j < g.numVertexes; j++) 14 { 15 if(g.arc[j] == 1 && !visited[j]) 16 { 17 DFS(g, j); //对为访问的邻接顶点递归调用 18 } 19 } 20 } 21 22 //邻接矩阵的深度遍历操作 23 void DFSTraverse(Graph g) 24 { 25 int i; 26 for(i = 0; i < g.numVertexes; i++) 27 { 28 visited = FALSE; //初始化所有顶点状态都是未访问过状态 29 } 30 for(i = 0; i < g.numVertexes; i++) 31 { 32 if(!visited) //对未访问的顶点调用DFS,若是连通图,只会执行一次 33 { 34 DFS(g,i); 35 } 36 } 37 }
如果使用的是邻接表存储结构,其DFSTraverse函数的代码几乎是相同的,只是在递归函数中因为将数组换成了链表而有不同,代码如下。
1 //邻接表的深度递归算法 2 void DFS(GraphList g, int i) 3 { 4 EdgeNode *p; 5 visited = TRUE; 6 printf("%c ", g->adjList.data); //打印顶点,也可以其他操作 7 p = g->adjList.firstedge; 8 while(p) 9 { 10 if(!visited[p->adjvex]) 11 { 12 DFS(g, p->adjvex); //对访问的邻接顶点递归调用 13 } 14 p = p->next; 15 } 16 } 17 18 //邻接表的深度遍历操作 19 void DFSTraverse(GraphList g) 20 { 21 int i; 22 for(i = 0; i < g.numVertexes; i++) 23 { 24 visited = FALSE; 25 } 26 for(i = 0; i < g.numVertexes; i++) 27 { 28 if(!visited) 29 { 30 DFS(g, i); 31 } 32 } 33 }
对比两个不同的存储结构的深度优先遍历算法,对于n个顶点e条边的图来说,邻接矩阵由于是二维数组,要查找某个顶点的邻接点需要访问矩阵中的所有元素,因为需要O(n2)的时间。而邻接表做存储结构时,找邻接点所需的时间取决于顶点和边的数量,所以是O(n+e)。显然对于点多边少的稀疏图来说,邻接表结构使得算法在时间效率上大大提高。
2.2 广度优先遍历
广度优先遍历,又称为广度优先搜索,简称BFS。图的广度优先遍历就类似于树的层序遍历了。
邻接矩阵做存储结构时,广度优先搜索的代码如下。
1 //邻接矩阵的广度遍历算法 2 void BFSTraverse(Graph g) 3 { 4 int i, j; 5 Queue q; 6 for(i = 0; i < g.numVertexes; i++) 7 { 8 visited = FALSE; 9 } 10 InitQueue(&q); 11 for(i = 0; i < g.numVertexes; i++)//对每个顶点做循环 12 { 13 if(!visited) //若是未访问过 14 { 15 visited = TRUE; 16 printf("%c ", g.vexs); //打印结点,也可以其他操作 17 EnQueue(&q, i); //将此结点入队列 18 while(!QueueEmpty(q)) //将队中元素出队列,赋值给 19 { 20 int m; 21 DeQueue(&q, &m); 22 for(j = 0; j < g.numVertexes; j++) 23 { 24 //判断其他顶点若与当前顶点存在边且未访问过 25 if(g.arc[m][j] == 1 && !visited[j]) 26 { 27 visited[j] = TRUE; 28 printf("%c ", g.vexs[j]); 29 EnQueue(&q, j); 30 } 31 } 32 } 33 } 34 } 35 } <span style="line-height:2;font-family:'sans serif', tahoma, verdana, helvetica;"> </span>
对于邻接表的广度优先遍历,代码与邻接矩阵差异不大, 代码如下。
1 //邻接表的广度遍历算法 2 void BFSTraverse(GraphList g) 3 { 4 int i; 5 EdgeNode *p; 6 Queue q; 7 for(i = 0; i < g.numVertexes; i++) 8 { 9 visited = FALSE; 10 } 11 InitQueue(&q); 12 for(i = 0; i < g.numVertexes; i++) 13 { 14 if(!visited) 15 { 16 visited = TRUE; 17 printf("%c ", g.adjList.data); //打印顶点,也可以其他操作 18 EnQueue(&q, i); 19 while(!QueueEmpty(q)) 20 { 21 int m; 22 DeQueue(&q, &m); 23 p = g.adjList[m].firstedge; 找到当前顶点边表链表头指针 24 while(p) 25 { 26 if(!visited[p->adjvex]) 27 { 28 visited[p->adjvex] = TRUE; 29 printf("%c ", g.adjList[p->adjvex].data); 30 EnQueue(&q, p->adjvex); 31 } 32 p = p->next; 33 } 34 } 35 } 36 } 37 }<span style="font-family:'sans serif', tahoma, verdana, helvetica;line-height:1.5;"> </span>
对比图的深度优先遍历与广度优先遍历算法,会发现,它们在时间复杂度上是一样的,不同之处仅仅在于对顶点的访问顺序不同。可见两者在全图遍历上是没有优劣之分的,只是不同的情况选择不同的算法。
版权所有,转载请注明转载地址:http://www.cnblogs.com/lihuidashen/p/4325282.html
作者: 李肖遥, 来源:面包板社区
链接: https://mbb.eet-china.com/blog/uid-me-3912462.html
版权声明:本文为博主原创,未经本人允许,禁止转载!
 /4
/4 
文章评论(0条评论)
登录后参与讨论